Computing a tangent plane
TLDRThis educational video script explains the concept of defining a function to create a plane in three-dimensional space. It emphasizes how to orient a plane by specifying partial derivatives and ensuring it passes through a given point. The script then illustrates finding the tangent plane to a graph by identifying a point on the graph, calculating the function's value at that point, and determining the partial derivatives with respect to x and y to match the slope of the tangent line. The process is clarified with a specific function example, simplifying the abstract mathematical concepts into a geometric understanding.
Takeaways
- 📚 The video discusses how to define a function for a plane that passes through a specified point and has a specified orientation.
- 📐 The orientation of the plane is determined by the values of its partial derivatives with respect to x and y.
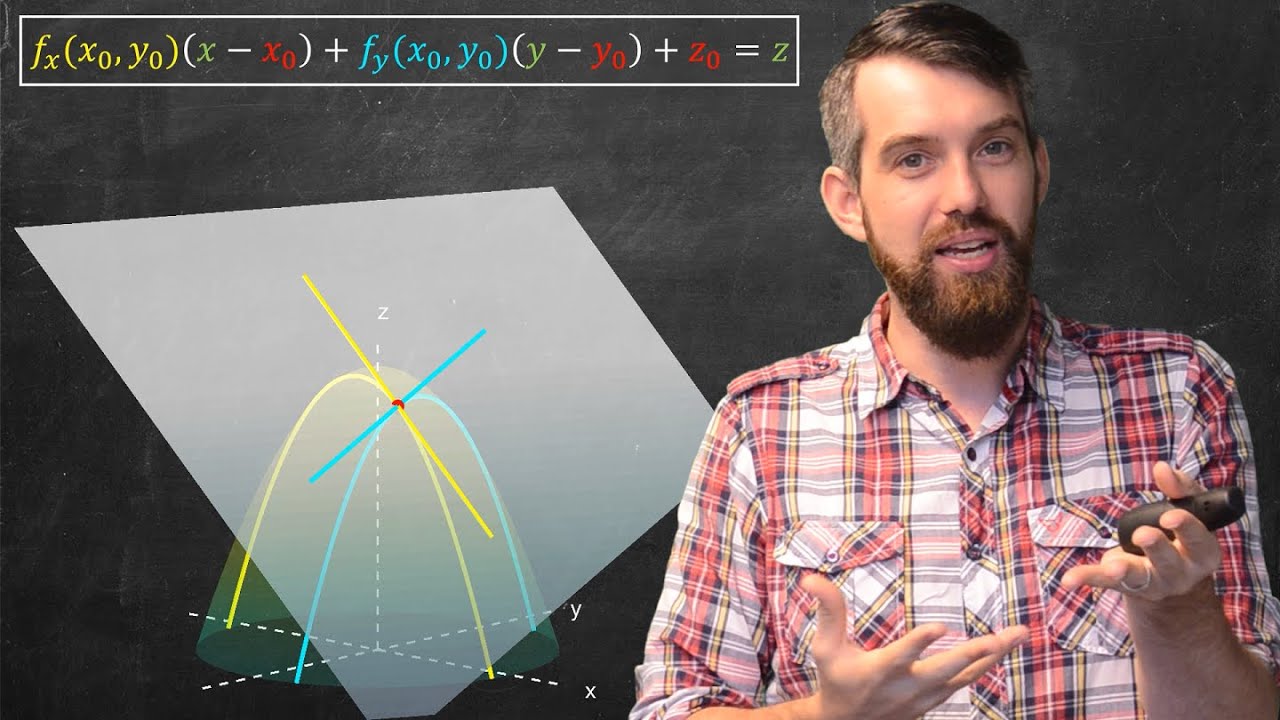
- 🔍 The general form of the plane function is a(x - x₀) + b(y - y₀) + z₀, where a, b are constants, and (x₀, y₀, z₀) is the specified point.
- 📈 The partial derivatives of the plane function with respect to x and y should be constants, which can be specified by the user.
- 👁️ When evaluating the function at (x₀, y₀), the terms involving (x - x₀) and (y - y₀) become zero, ensuring the plane passes through the point (x₀, y₀, z₀).
- 🔑 To find the tangent plane to a graph, you specify a point on the graph with coordinates (x₁, y₁) and calculate the z-coordinate using the function's value at that point.
- 📉 The function used in the video is f(x, y) = 3 - (1/3)(x² - y²), and the point on the graph is determined by evaluating this function at (1, -2).
- 📌 The tangent plane's formula is derived from the linear function that passes through the specified point and has the same partial derivatives as the original function at that point.
- 📊 The partial derivative of f with respect to x at (1, -2) is -2/3, and for y, it is 4, which are used to determine the constants a and b in the tangent plane equation.
- 🧩 The final formula for the tangent plane includes the input point (1, -2), the function's value at that point, and the partial derivatives to ensure correct orientation.
- 📚 Understanding the geometric meaning of each term in the tangent plane formula helps in visualizing and comprehending the process of finding the tangent plane to a graph.
Q & A
What is the main topic discussed in the video script?
-The main topic is about defining a function that represents a plane, specifically one that passes through a specified point and has a specified orientation, with a focus on finding the tangent plane to a graph.
How is the orientation of the plane specified in the script?
-The orientation of the plane is specified through certain partial derivative information, which allows the plane to have a constant partial derivative with respect to x and another constant partial derivative with respect to y.
What is the significance of the point (x₀, y₀, z₀) in the context of the script?
-The point (x₀, y₀, z₀) is significant because it represents the specific point in space that the plane must pass through. It is used to define the constants in the plane equation and to ensure that the function evaluates to z₀ when x and y are set to x₀ and y₀, respectively.
What is the purpose of the constants a and b in the plane equation?
-The constants a and b in the plane equation are coefficients that, when multiplied by (x - x₀) and (y - y₀) respectively, help define the plane's orientation in the x and y directions. They are determined by the partial derivatives of the function with respect to x and y at the point (x₀, y₀).
How does the script describe the process of finding the tangent plane to a graph?
-The script describes the process by first identifying a point on the graph, then evaluating the function at that point to get the z-coordinate. It then involves calculating the partial derivatives of the function with respect to x and y at that point, which are used as the coefficients a and b in the tangent plane equation.
What is the function f(x, y) used in the script to demonstrate the concept?
-The function f(x, y) used in the script is f(x, y) = 3 - (1/3) * (x^2 - y^2), which is a specific example to illustrate the process of finding the tangent plane.
How is the z-coordinate of the tangent plane determined?
-The z-coordinate of the tangent plane is determined by evaluating the original function f(x, y) at the specified point (x₀, y₀), which gives the value of z at that point on the graph.
What role do the partial derivatives play in defining the tangent plane?
-The partial derivatives with respect to x and y play a crucial role in defining the tangent plane as they provide the slopes of the tangent lines in the x and y directions at the specified point, which the tangent plane must match.
How does the script explain the relationship between the tangent plane and the original function's graph?
-The script explains that the tangent plane should intersect the original function's graph along the same tangent lines as determined by the partial derivatives at the specified point, ensuring that the plane has the same orientation as the graph at that point.
What is the final formula for the tangent plane as described in the script?
-The final formula for the tangent plane is a linear function of x and y that includes the constants a and b, which are the partial derivatives of the original function evaluated at the specified point, along with the z-coordinate obtained by evaluating the original function at that point.
Outlines
📚 Defining a Plane Function with Specified Orientation
This paragraph introduces the concept of defining a function that represents a plane in three-dimensional space. The plane is designed to pass through a specific point, which is defined by the constants x_nought, y_nought, and z_nought. The orientation of the plane is determined by the partial derivatives with respect to x and y. The speaker simplifies the explanation by abstracting the concept and then provides a formula for the plane that includes constants a and b, which are related to the partial derivatives. The formula is further explained by showing how it ensures the plane passes through the specified point when the variable values are substituted with the constants.
📐 Constructing the Tangent Plane to a Graph
The second paragraph delves into the process of finding the tangent plane to a graph at a given point. The point on the graph is specified by two coordinates, x and y, and the z coordinate is determined by the function's output at that point. The function used in the example is f(x, y) = 3 - (1/3) * (x^2 - y^2). To construct the tangent plane, the speaker explains the need to match the partial derivatives of the original function with those of the tangent plane in the x and y directions. The partial derivatives of the function with respect to x and y are computed and then used to determine the constants a and b for the tangent plane equation. The process involves evaluating the function at the specified point and using the computed derivatives to ensure the tangent plane aligns with the graph at that point.
Mindmap
Keywords
💡Function
💡Graph
💡Plane
💡Partial Derivative
💡Tangent Plane
💡Specified Point
💡Constant
💡Derivative
💡Orientation
💡Z Coordinate
💡Linear Function
Highlights
Introduction to defining a function whose graph is a plane passing through a specified point with a particular orientation.
Explanation of using partial derivative information to specify the orientation of a plane.
General formula for the plane: a(x - x₀) + b(y - y₀) + z₀, where x₀, y₀, and z₀ are constants representing a specific point.
Importance of ensuring the function passes through a given point by setting the partial derivatives correctly.
Discussion on how the plane's partial derivatives with respect to x and y are constants that can be specified.
Introduction to finding the tangent plane to a graph at a specific point.
Clarification that specifying only x and y coordinates is sufficient since z is determined by the function's output.
Definition of the function used in the example: f(x, y) = 3 - (1/3)x² - y².
Calculation of the specific point on the graph by evaluating f(1, -2), resulting in z = -4/3.
Derivation of the partial derivative of f with respect to x: -2/3x, and its evaluation at the point (1, -2).
Determination of the partial derivative with respect to x at the point (1, -2) as -2/3.
Derivation of the partial derivative of f with respect to y: -2y, and its evaluation at the point (1, -2).
Determination of the partial derivative with respect to y at the point (1, -2) as 4.
Construction of the tangent plane equation with the determined constants: -2/3(x - 1) + 4(y + 2) - 4/3.
Emphasis on the importance of understanding each component of the tangent plane formula for correct specification and orientation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: