Lec 5: Parametric equations for lines and curves | MIT 18.02 Multivariable Calculus, Fall 2007
TLDRThis lecture delves into the geometrical concepts of 3x3 linear systems, planes, and lines, exploring the conditions for unique, no, or infinite solutions. It introduces parametric equations of lines as trajectories of moving points, demonstrating how to derive them using two points or a point and a directional vector. The lecture further applies these concepts to analyze the intersection of lines and planes, and illustrates the use of parametric equations in describing complex curves, such as cycloids, formed by a point on a rolling wheel. The discussion includes a detailed examination of the cycloid's properties, including its behavior near the bottom point, using approximations and Taylor expansions to reveal the curve's infinite slope at the origin.
Takeaways
- 📚 The lecture discusses the geometric interpretation of 3x3 linear systems, focusing on the intersection of planes and the conditions for unique, no, or infinite solutions.
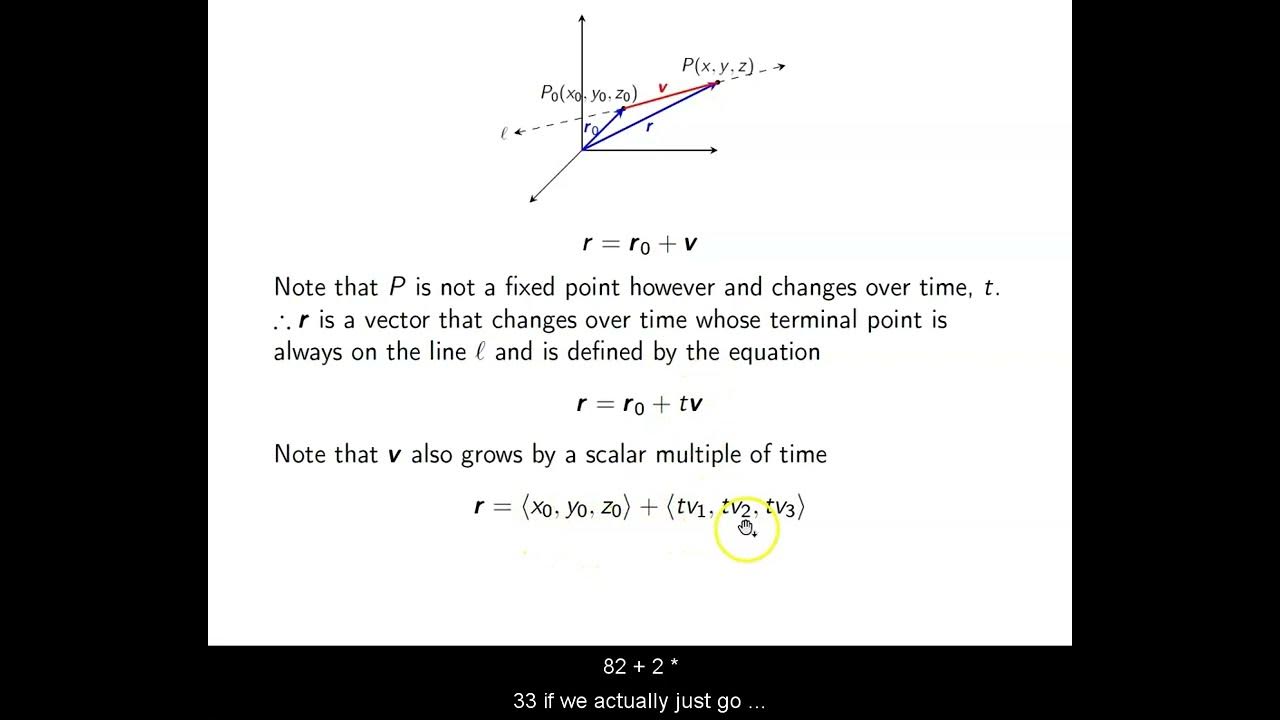
- 🤔 It explores the concept of lines as trajectories of moving points and introduces parametric equations as a way to describe these lines in space.
- 📍 The script explains how to find parametric equations for a line given two points or a point and a direction vector, using the example of points (-1,2,2) and (1,3,-1).
- 🔍 It demonstrates how to determine the intersection of a line and a plane using parametric equations, with the example of the plane equation x + 2y + 4z = 7.
- 📈 The lecture also touches on the implications of the coefficient of 't' in parametric equations, relating it to whether a line is parallel to a plane or lies within it.
- 🌐 The concept of parametric equations is extended to describe more complex motions and curves, such as the cycloid, which is the path traced by a point on a rolling wheel.
- 🚴♂️ A cycloid is illustrated as the trajectory of a point on the circumference of a wheel rolling without slipping on a flat surface, creating a characteristic curve.
- 📉 The script uses vector addition to break down the position of a point on the cycloid into simpler components, relating it to the angle of rotation of the wheel.
- 📚 It explains how to parameterize the motion of the point on the cycloid using the angle of rotation, leading to parametric equations for the cycloid in terms of this angle.
- 🔎 The lecture concludes with an exploration of the behavior of the cycloid near its bottom points, using Taylor expansions to approximate the parametric equations for small angles.
- 📉 Finally, it reveals that the cycloid has a vertical tangent at the bottom points, indicating an infinite slope, which was determined by analyzing the ratio of y to x near the origin.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is the geometric and algebraic understanding of lines in 3D space, specifically through parametric equations and their applications, such as determining the intersection of a line and a plane.
Why are parametric equations of lines useful in 3D space?
-Parametric equations of lines are useful because they provide a convenient way to describe the trajectory of a moving point in space, making it easier to visualize and calculate positions along the line at different times.
How can you represent a line in space using two points?
-A line in space can be represented by two points lying on it. These points can then be used to derive the parametric equations of the line, which describe all points on the line as a function of a parameter, typically time or a scalar parameter.
What is the significance of the vector between two points on a line in parametric equations?
-The vector between two points on a line represents the direction of the line. In parametric equations, this vector, when scaled by the parameter 't', shows how the moving point progresses along the line.
How can you determine if a line intersects with a plane?
-To determine if a line intersects with a plane, you can plug the parametric equations of the line into the equation of the plane. If there exists a value of the parameter 't' for which the plane equation is satisfied, the line intersects the plane at that point.
What does it mean if the moving point never equals the plane in the context of the script?
-If the moving point never equals the plane, it implies that the line is parallel to the plane and does not intersect it at any point. This situation occurs when the resulting expression from plugging the parametric equations into the plane's equation never equals zero.
What is a cycloid and how is it related to the script's discussion on parametric equations?
-A cycloid is the curve traced by a point on the rim of a rolling wheel. It is related to the script's discussion as it provides an example of using parametric equations to describe the motion of a point in a more complex scenario, showcasing the versatility of parametric equations.
How does the script use the concept of a wheel rolling without slipping to explain parametric equations?
-The script uses the concept of a wheel rolling without slipping to explain that the distance the wheel travels on the ground (OA) is equal to the arc length on the circumference of the wheel from a point P to the point of contact (A), which is expressed as a(theta), where 'a' is the radius of the wheel and 'theta' is the angle of rotation.
Why does the script suggest rescaling measurements by the radius of the wheel?
-Rescaling measurements by the radius of the wheel simplifies the parametric equations of the cycloid by setting the length unit equal to the radius, thus making the equations more manageable and easier to analyze, especially when considering small angles.
What does the script reveal about the behavior of the cycloid near the bottom point using Taylor expansions?
-The script reveals that near the bottom point of the cycloid, the slope of the curve approaches infinity, indicating a vertical tangent. This is determined by using Taylor expansions to approximate the sine and cosine functions for small angles, showing that the y-component of the curve dominates near the origin.
Outlines
📚 Introduction to Linear Systems and Parametric Equations
The script begins with a review of 3x3 linear systems and their geometric interpretation in terms of intersecting planes. It explains scenarios where a unique solution may not exist, such as when the intersection line of two planes is parallel to the third plane, leading to either no solution or infinitely many solutions. The lecture then transitions into discussing the equations of lines, initially describing them as intersections of two planes but quickly shifting to the parametric representation of lines as a more convenient approach. The concept of a line as a trajectory of a moving point is introduced, setting the stage for the exploration of parametric equations of lines.
🔍 Parametric Equations of Lines and Their Derivation
This paragraph delves into the specifics of parametric equations of lines, illustrating how to derive them using two points on the line or a point and a directional vector. It provides an example using two points in space, (-1,2,2) and (1,3,-1), to demonstrate the process of finding the parametric equations. The explanation includes the concept of a moving point on the line, described by its position at various times, and the method to find the position of this point at any given time t. The paragraph concludes with the derivation of the parametric equations for the line defined by the two example points.
🤔 Analyzing Line-Plane Intersections Using Parametric Equations
The script continues with an application of parametric equations to determine the relative positions of a line and a plane. It introduces a plane with the equation x + 2y + 4z = 7 and explores whether a given line intersects this plane and, if so, where. The discussion involves evaluating the plane equation at two points on the line to determine if they are on the same side, opposite sides, or if one lies on the plane. The paragraph also includes an interactive element where the audience is asked to vote on the relative positions, followed by a clarification of the correct answer based on the calculations.
📐 Determining Intersection Points Between Lines and Planes
Building on the previous discussion, this paragraph focuses on finding the exact point of intersection between a line and a plane using parametric equations. It guides through the process of substituting the parametric equations of the line into the plane's equation and solving for the parameter t that satisfies the plane equation. The example provided finds that the line intersects the plane at t = 1/2, and the corresponding point of intersection is calculated. The paragraph also addresses what happens if no solution exists, indicating that the line would be parallel to or contained within the plane.
🌐 Exploring Parametric Equations for Curves and Motion
The script broadens the application of parametric equations to model not just lines, but any curve or trajectory of a moving point. It introduces the concept with an example of a cycloid, a curve traced by a point on the rim of a rolling wheel. The paragraph explains the physical setup of a wheel rolling on a horizontal surface and the trajectory of a point on the wheel's circumference. It sets the stage for deriving the parametric equations for the cycloid in subsequent paragraphs.
🎡 Deriving Parametric Equations for a Cycloid
This paragraph continues the exploration of cycloids by attempting to derive their parametric equations. It introduces the parameters of the problem, such as the radius of the wheel and the angle of rotation, and discusses the relationship between the distance traveled by the wheel and the arc length on the circumference. The explanation involves breaking down the position vector of the point on the wheel into simpler vectors, which are then used to express the parametric equations for the cycloid's curve.
🔬 Investigating the Behavior of a Cycloid Near Its Bottom Point
The script examines the behavior of the cycloid near its bottom point, a feature that appears pointy in graphical representations. It discusses the possibility of the curve having a corner, a smooth transition, or even a loop at that point. The paragraph uses the derived parametric equations and simplifies them by rescaling with the wheel's radius as the unit of length. It then applies Taylor expansions to approximate the sine and cosine functions for small angles, providing insight into the curve's behavior near the bottom point.
📉 Analyzing the Tangent Behavior of a Cycloid at the Origin
This paragraph concludes the analysis of the cycloid's behavior near the origin by calculating the ratio of the y-component to the x-component of the parametric equations. It shows that as the angle approaches zero, the slope of the curve becomes infinite, indicating a vertical tangent at the origin. The explanation clarifies that the dominant motion near the origin is vertical, confirming the presence of a cusp, or a pointy feature, in the curve's geometry.
📅 Conclusion and Upcoming Practice Exams
The script concludes with an announcement about the end of the lecture and the plan for the upcoming week. It informs the audience that practice exams will be provided for the following week's test, which will take place on Tuesday. The paragraph serves as a reminder and a transition to the next part of the course.
Mindmap
Keywords
💡Parametric Equations
💡Line in Space
💡Plane Equation
💡Intersection
💡Cycloid
💡Vector
💡Normal Vector
💡Dot Product
💡Taylor Expansion
💡Vertical Tangent
Highlights
Introduction to geometric interpretation of 3x3 linear systems and conditions for unique/non-unique solutions.
Exploration of line equations through parametric representation as a trajectory of a moving point.
Method to describe a line using two points or a point and a vector parallel to the line.
Technique to find all points on a line using parametric equations derived from two given points.
Explanation of how to determine if a point is on a plane using the plane's equation.
Process to determine the intersection of a line and a plane using parametric equations.
Understanding the implications of a line being parallel to or contained in a plane.
Introduction to cycloids as a trajectory of a point on a rolling wheel.
Derivation of parametric equations for a cycloid based on the angle of wheel rotation.
Use of vector addition to simplify the calculation of a point's position on a cycloid.
Application of Taylor expansion to approximate the behavior of a cycloid near its bottom point.
Analysis of the slope and behavior of a cycloid at the bottom point revealing a vertical tangent.
Discussion on the practical visualization of a cycloid's curve and its characteristics.
Engagement with the audience to understand the conceptualization of a cycloid's trajectory.
Final remarks on the practical exam preparation and upcoming schedule.
Transcripts
Browse More Related Video

Calculus 3: Equations of Lines and Planes (Video #5) | Math with Professor V

Ch. 10.1 Systems of Linear Equations in Two Variables

Calculus 3: Tangent Planes and Linear Approximation (Video #14) | Math with Professor V
Ch. 9.6 Equations of Lines and Planes

Calculus 1 Lecture 0.1: Lines, Angle of Inclination, and the Distance Formula

Calculus 3: Lecture 11.5 Lines and Planes in Space
5.0 / 5 (0 votes)
Thanks for rating: