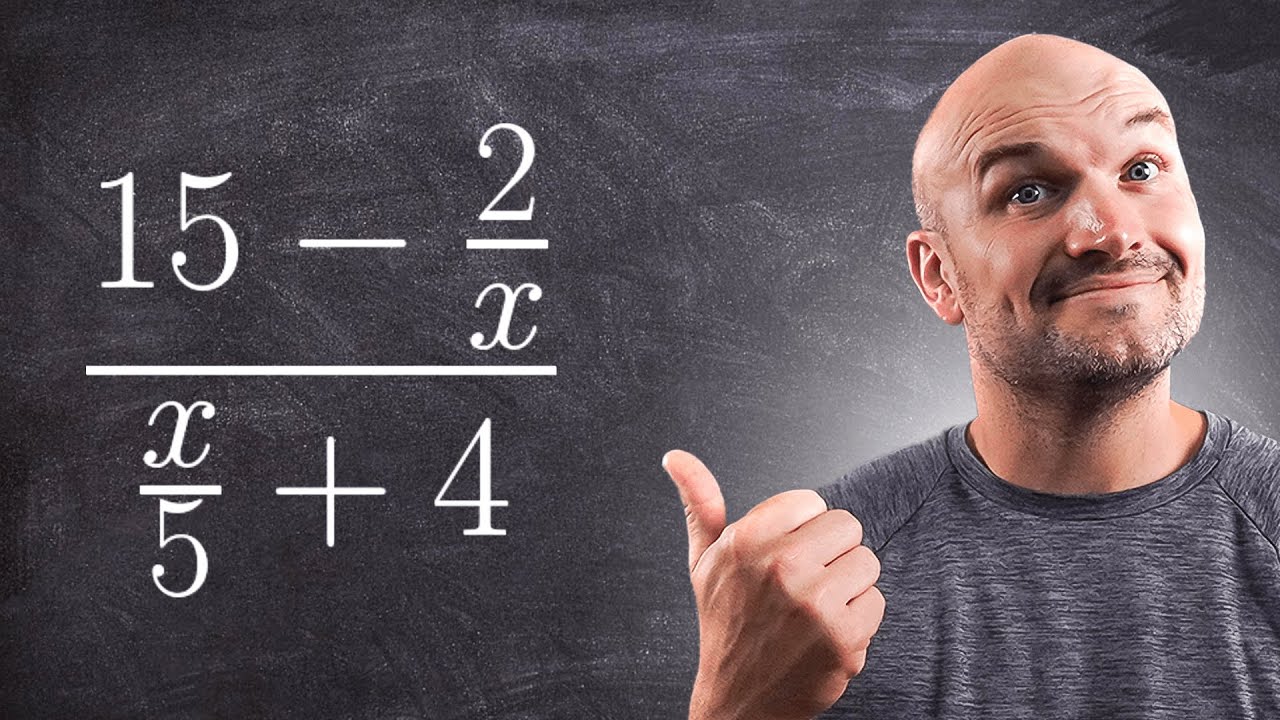Ch. 1.4 Rational Expressions
TLDRThis video script covers the fundamentals of rational expressions, including their definition, arithmetic operations, and simplification techniques. It emphasizes the importance of factoring and finding the least common denominator (LCD) for adding and subtracting fractions. The instructor also explains how to handle complex fractions through both arithmetic simplification and the LCD method, highlighting common errors to avoid in algebraic manipulations.
Takeaways
- 📚 The lesson is a review on rational expressions, which are algebraic expressions in fraction form where both numerator and denominator are polynomials.
- 🚫 Division by zero is undefined in rational expressions, so the domain excludes values that make the denominator zero.
- 🔍 Simplifying rational expressions involves factoring both the numerator and the denominator first, which helps in identifying common factors for cancellation.
- 🧩 Arithmetic on rational expressions is similar to arithmetic on regular fractions, with the added complexity of dealing with polynomials.
- 🔑 The process of finding a common denominator (LCM) is crucial for adding or subtracting rational expressions and involves considering all factors in the denominators.
- 📉 When simplifying, it's important to factor polynomials correctly and then identify what is missing in the current base to build the LCM.
- 🔄 The concept of LCM is applied to both numerical coefficients and variable exponents when combining terms with different denominators.
- 📝 The script provides a step-by-step guide on how to find the LCM for algebraic expressions, emphasizing the importance of factoring and identifying missing terms.
- ✂️ The process of simplifying complex fractions can be done by either simplifying each part separately or by using the LCM method to clear the denominators.
- 🚫 Common mistakes when dealing with rational expressions include incorrect distribution of powers and roots, and misunderstanding how to properly cancel terms.
- 🔍 The script emphasizes the importance of practice in mastering the techniques for working with rational expressions and avoiding common errors.
Q & A
What is the main topic of the video script?
-The main topic of the video script is rational expressions, including their definition, arithmetic operations, simplification, and working with complex fractions.
What are rational numbers in the context of this script?
-In the context of this script, rational numbers are integers over another integer, also known as fractions, and are used to discuss rational expressions in algebra.
What is the condition for the denominator in a rational expression?
-The denominator in a rational expression cannot be zero, as division by zero is undefined.
How is the domain of a rational expression determined?
-The domain of a rational expression is determined by all real numbers that can be plugged into the expressions in the numerator and denominator without making the denominator equal to zero.
What is the first step in simplifying rational expressions?
-The first step in simplifying rational expressions is to factor everything, which includes factoring polynomials in the numerator and denominator.
How does arithmetic on rational expressions differ from arithmetic on regular numbers?
-Arithmetic on rational expressions is the same as on regular numbers, but the numbers involved are in algebraic form and may require additional steps like factoring before performing operations.
What is the purpose of finding the least common multiple (LCM) when working with fractions?
-The purpose of finding the LCM when working with fractions is to create a common denominator, which is necessary for adding or subtracting fractions.
How is the LCM used to simplify complex fractions?
-The LCM is used to simplify complex fractions by multiplying the entire rational expression by a form of one, where the one is made up of the LCM over the LCM, thus simplifying it to a single rational expression.
What are common errors made when working with rational expressions?
-Common errors include misunderstanding the distribution of powers and roots across addition or subtraction, incorrectly simplifying expressions by not properly creating a common denominator, and misapplying the cancellation rules.
What is the preferred method for simplifying complex fractions according to the script?
-The preferred method for simplifying complex fractions according to the script is the clearing denominators method, which involves multiplying by the reciprocal of the denominator to simplify the expression.
Outlines
📚 Introduction to Rational Expressions
The instructor begins with an introduction to rational expressions, explaining that they are algebraic expressions in fraction form where both the numerator and the denominator are polynomials. The domain of a rational expression is all real numbers except those that make the denominator zero. The importance of factoring in simplifying rational expressions is emphasized, as well as the arithmetic operations that can be performed on them, such as addition, subtraction, multiplication, and division. The session aims to review material from an Algebra 2 class, focusing on the foundational concepts of rational expressions.
🔍 Building the Least Common Multiple (LCM) for Rational Expressions
This paragraph delves into the process of finding the least common multiple (LCM) for the denominators of rational expressions, which is crucial for creating a common denominator when adding or subtracting fractions. The instructor illustrates how to build the LCM step by step by identifying the missing factors from the current base and incorporating them to ensure the LCM can generate all original denominators independently. Examples are given to demonstrate the process of factorization and how to determine what is missing to complete the LCM for a set of algebraic expressions.
📘 Factoring and Simplifying Polynomials in Rational Expressions
The instructor discusses the importance of factoring polynomials within rational expressions and provides a step-by-step method for simplifying complex rational expressions. The process involves factoring each polynomial in the denominator and numerator, identifying common factors, and then simplifying by canceling out common terms. The paragraph includes examples of factoring binomials and trinomials and emphasizes the ease of simplifying once the expressions are factored into their simplest form.
📖 Simplifying Complex Fractions and Common Errors
This section covers the simplification of complex fractions, which are rational expressions within other rational expressions. The instructor presents two methods for simplification: simplifying the numerator and denominator separately and then dividing, or using the least common multiple (LCM) method to clear the denominators. The paragraph also highlights common mistakes made when simplifying rational expressions, such as incorrect distribution of powers and roots, and the incorrect assumption that certain functions distribute across addition or subtraction.
📌 Common Mistakes in Rational Expressions
The instructor provides a guide to common errors encountered when working with rational expressions, such as the incorrect assumption that an exponent or root can be distributed across addition or subtraction. The paragraph clarifies that functions like exponents and roots do not distribute in this way and emphasizes the importance of recognizing that the nth root of a sum is not the same as the sum of the nth roots. Additionally, the instructor cautions against the mistake of simplifying 1/(a+b) to 1/a + 1/b, which is incorrect without a common denominator.
Mindmap
Keywords
💡Rational Expressions
💡Domain
💡Factoring
💡Arithmetic Operations
💡Common Denominator
💡Lowest Common Multiple (LCM)
💡Difference of Squares
💡Simplification
💡Complex Fractions
💡Clearing Denominators
💡Common Errors
Highlights
Introduction to rational expressions as fractions with polynomials in the numerator and denominator.
Explanation of the domain of a rational expression, excluding values that make the denominator zero.
Importance of factoring polynomials in the numerator and denominator before simplifying rational expressions.
Arithmetic operations on rational expressions are analogous to those on regular fractions.
Building the least common multiple (LCM) for denominators step by step from their factors.
Method to find the LCM for algebraic expressions by taking the highest powers of variables present.
Simplification of complex fractions by either combining into a single rational expression or using the LCM method.
Clearing the denominators as a powerful method in algebra for dealing with complex fractions.
Avoiding common errors such as misapplying the distributive property to exponents and roots.
Clarification that the nth root of a sum does not simplify by distributing the root across terms.
Emphasizing the incorrectness of simplifying 1/(a+b) to 1/a + 1/b without a common denominator.
Guideline against assuming that terms can be canceled without proper common factors in the numerator.
Review of rational expressions as a recap from an Algebra 2 class, indicating the intended audience's prior knowledge.
Illustration of the process to find the LCM for a set of algebraic expressions with a step-by-step example.
Demonstration of simplifying a complex rational expression by factoring and canceling terms efficiently.
Highlight of the correct approach to work with complex fractions using arithmetic or the LCM method.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: