STANDARD EQUATION OF AN ELLIPSE IN A GENERAL FORM

WOW MATH
7 Oct 202212:37
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial guides viewers through the process of converting standard form equations into their general form, which is expressed as ax^2 + by^2 + cx + dy + e = 0. The instructor provides step-by-step examples, starting with finding the least common denominator (LCD) and then multiplying through by this LCD to eliminate fractions. Each example is methodically worked through, showing the algebraic manipulation required to reach the general form. The video is a practical resource for those looking to understand and apply the transformation of quadratic equations.

Takeaways
  • 📚 The video is a tutorial on converting standard form equations to general form.
  • 🔍 It begins with an explanation of the general form equation: ax^2 + by^2 + cx + dy + e = 0.
  • 📐 The first example involves converting the equation (x + 1) / 2 + (y - 1) / 3 = 1 to general form by finding a common denominator and multiplying through.
  • 📈 The process includes expanding and simplifying the equation to get x^2 + 2x + 1 + 3y^2 - 4y + 4 = 9.
  • ✍️ The second example shows the conversion of (x - 1) / 20 + y^2 / 10 = 1 by multiplying through by 20 to eliminate the denominators.
  • 📉 The third example starts with x^2 / 4 + (y + 4) / 5 = 1 and uses the LCD of 20 to convert it to general form.
  • 📌 The fourth example demonstrates converting (x + 2) / 2 + (y - 2) / 4 = 8 by finding a common denominator and multiplying.
  • 🔢 Each step involves careful attention to detail, especially when multiplying through by the LCD to clear fractions.
  • 📘 The tutorial emphasizes the importance of correctly applying algebraic principles to achieve the general form.
  • 🎓 The video concludes by summarizing the steps taken to transform the standard equations into the general form, reinforcing the learning objectives.
Q & A

  • What is the standard form of a conic section equation?

    -The standard form of a conic section equation is \( ax^2 + by^2 + cx + dy + e = 0 \).

  • What is the first step in converting a conic section equation to the general form?

    -The first step is to find the least common denominator (LCD) to simplify the equation.

  • How is the LCD used in the process of converting equations?

    -The LCD is used to multiply both sides of the equation to eliminate fractions and simplify the terms.

  • What is the equation of the first example given in the transcript?

    -The first example is \( x + \frac{1}{2} + y - \frac{1}{3} = 1 \).

  • What is the result of multiplying the first example by the LCD?

    -After multiplying by the LCD, the equation becomes \( 3y^2 + 2x - 12y - 9 = 0 \).

  • What is the equation of the second example in the transcript?

    -The second example is \( x - \frac{1}{2} + \frac{y^2}{10} = 1 \).

  • How is the second example equation transformed to the general form?

    -The equation is multiplied by 20 to clear the fractions, resulting in \( x^2 - 2x + 2y^2 - 2 - 20 = 0 \).

  • What is the equation of the third example provided in the transcript?

    -The third example is \( \frac{x^2}{4} + \frac{y + 4}{5} = 1 \).

  • What is the LCD for the third example and how is it used?

    -The LCD for the third example is 20. It is used to multiply the equation to get \( 5x^2 + 4y^2 + 8y + 32 - 20 = 0 \).

  • What is the final equation obtained from the third example after simplification?

    -The final equation is \( 5x^2 + 4y^2 + 8y - 20 = 0 \).

  • What is the fourth example equation in the transcript?

    -The fourth example is \( x + \frac{2}{2} + y - \frac{2}{4} = 8 \).

  • How is the fourth example equation converted to the general form?

    -The equation is multiplied by 8 to clear the fractions, resulting in \( 4x^2 + 2y^2 + 16x - 8y - 16 = 0 \).

  • What is the final step in the process described in the transcript?

    -The final step is to simplify the equation obtained after multiplying by the LCD to its general form.

Outlines
00:00
📚 Introduction to Standard Equations in General Form

This paragraph introduces the task of converting standard form equations into a general form, which is represented as ax^2 + by^2 + c x + d y = 0. It begins with an example equation, (x + 1)^2 + (y - 1)(2/3) = 1, and explains the process of finding the least common denominator (LCD) and multiplying the equation by 9 to achieve the general form. The example concludes with the transformed equation: 3y^2 + 2x - 12y - 9 = 0.

05:08
🔍 Transforming Equations: Examples and Steps

The second paragraph continues with the theme of transforming equations into the general form. It provides another example, x^2/20 + y^2/10 = 1, and details the steps to multiply by 20 to clear the fractions. The process includes simplifying the equation to 20x^2 + 2y^2 - 2x - 20 = 0. The paragraph also mentions a third example involving x^2/4 + y + 4(2/5) = 1, which is transformed by multiplying by 20 to yield 5x^2 + 4y^2 + 4y + 8 = 20.

10:09
📘 Final Examples and Conclusion

The final paragraph wraps up the discussion with additional examples of transforming equations into the general form. It starts with an equation involving x + 2(2/2) + y - 2(2/4) = 8, and after multiplying by 8, the equation becomes 4x^2 + 2y^2 + 16x - 8y - 16 = 0. The paragraph also includes a brief mention of the process for another equation, but it seems to be cut off, indicating an incomplete explanation. The video concludes with a summary of the process and a thank you note to the viewers.

Mindmap
Keywords
💡Standard Equation
A standard equation is a form of an equation that represents a geometric shape, such as an ellipse or hyperbola, in a specific format. In the context of the video, the standard equation is being transformed into a general form to facilitate mathematical analysis. For example, the script mentions converting equations like 'x plus one over nine plus y minus one over three is equal to one' into a general form.
💡General Form
The general form of an equation is a way of writing an equation that makes it easier to identify and analyze the components of the equation. The video's theme revolves around converting standard equations into this general form, which is typically represented as 'Ax^2 + By^2 + Cx + Dy + E = 0'. This form allows for a systematic approach to solving or analyzing the equation.
💡Least Common Denominator (LCD)
The least common denominator is the smallest multiple that is evenly divisible by each of the numbers involved in a mathematical expression. In the video, the LCD is used to simplify equations by ensuring that all terms have a common denominator, making it easier to combine and manipulate them. For instance, the script refers to finding an LCD to combine terms like 'x plus one over nine' and 'y minus two over three'.
💡Multiplying Equations
Multiplying equations is a mathematical operation where each term in an equation is multiplied by the same number or expression. In the video, this process is used to clear fractions and to transform the standard equation into the general form. The script illustrates this by showing how equations are multiplied by a certain factor to eliminate denominators and achieve the desired form.
💡Coefficients
Coefficients are numerical factors that multiply variables in an algebraic expression or equation. In the context of the video, coefficients are used to describe the relationship between the variables x and y in the general form of the equation. The script provides examples of how coefficients are determined, such as 'a x squared' and 'b y squared', in the general equation.
💡Linear Terms
Linear terms in an equation are terms that involve the first power of a variable. In the video, linear terms like 'c x' and 'd y' are part of the general form equation and are manipulated to achieve the desired format. The script shows how these terms are included and combined with other terms to form the complete equation.
💡Constant Term
A constant term in an equation is a term that does not contain any variables. It is typically found on one side of the equation and is used to balance it. In the video, the constant term 'E' is part of the general form equation and is set equal to zero to satisfy the equation's requirements.
💡Binomial
A binomial is an algebraic expression that contains two terms. In the video, binomials such as 'x plus one' and 'y minus two' are used within the context of equations that are being transformed. The script demonstrates how these binomials are manipulated through multiplication and combination to form the general equation.
💡Distributive Property
The distributive property is a fundamental principle in algebra that states that a(b + c) = ab + ac. This property is used in the video to expand expressions and simplify equations. For example, when multiplying 'x squared plus two x plus one' by a constant, the distributive property is applied to each term within the binomial.
💡Equation Transformation
Equation transformation refers to the process of changing an equation from one form to another to simplify it or to reveal its underlying structure. The main theme of the video is transforming standard equations into the general form, which is a specific type of equation transformation. The script provides step-by-step examples of how this transformation is carried out.
Highlights

Introduction to converting standard equations to general form.

Explanation of the general form equation: ax^2 + by^2 + cx + dy + e = 0.

First example: Converting (x + 1)^2 / 9 + (y - 1)(2/3) = 1 to general form.

Step-by-step process of finding the least common denominator (LCD).

Multiplying both sides of the equation to eliminate fractions.

Resulting general form: x^2 + 2x + 1 + 3y^2 - 4y + 4 = 9.

Second example: Converting (x - 1)^2 / 20 + y^2 / 10 = 1 to general form.

Adjusting coefficients to find the LCD and simplifying the equation.

General form achieved: x^2 - 2x - 2 + 2y^2 = 20.

Third example: Converting x^2 / 4 + (y + 4)(2/5) = 1 to general form.

Using LCD to multiply and simplify the equation.

Final general form: 5x^2 + 4y^2 + 4y + 8 = 20.

Fourth example: Converting (x + 2)(2/2) + (y - 2)(2/4) = 8 to general form.

Multiplying by the LCD to clear fractions and simplify.

General form obtained: 4x^2 + 2y^2 + 16x - 8y - 16 = 0.

Summary of the method for transforming standard equations to general form.

Thank you message and conclusion of the lesson.

Transcripts

Browse More Related Video

GENERAL EQUATION OF THE HYPERBOLA IN STANDARD FORM || PRE-CALCULUS

STANDARD EQUATION OF ELLIPSE TO GENERAL FORM | PRE-CALCULUS

STANDARD EQUATION OF PARABOLA TO GENERAL FORM

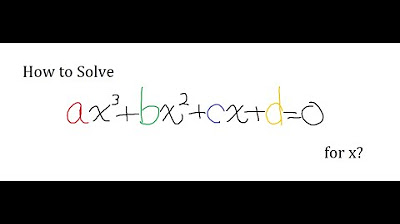
[Algebra] Is there any cubic formula?

Transforming Standard Form to General Form of Parabola | @ProfD

CIRCLE | TRANSFORMING GENERAL FORM TO STANDARD FORM | PROF D

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsAlgebraEquationsTutorialEducationGeneral FormStandard FormEquation TransformationMath LessonsOnline Learning