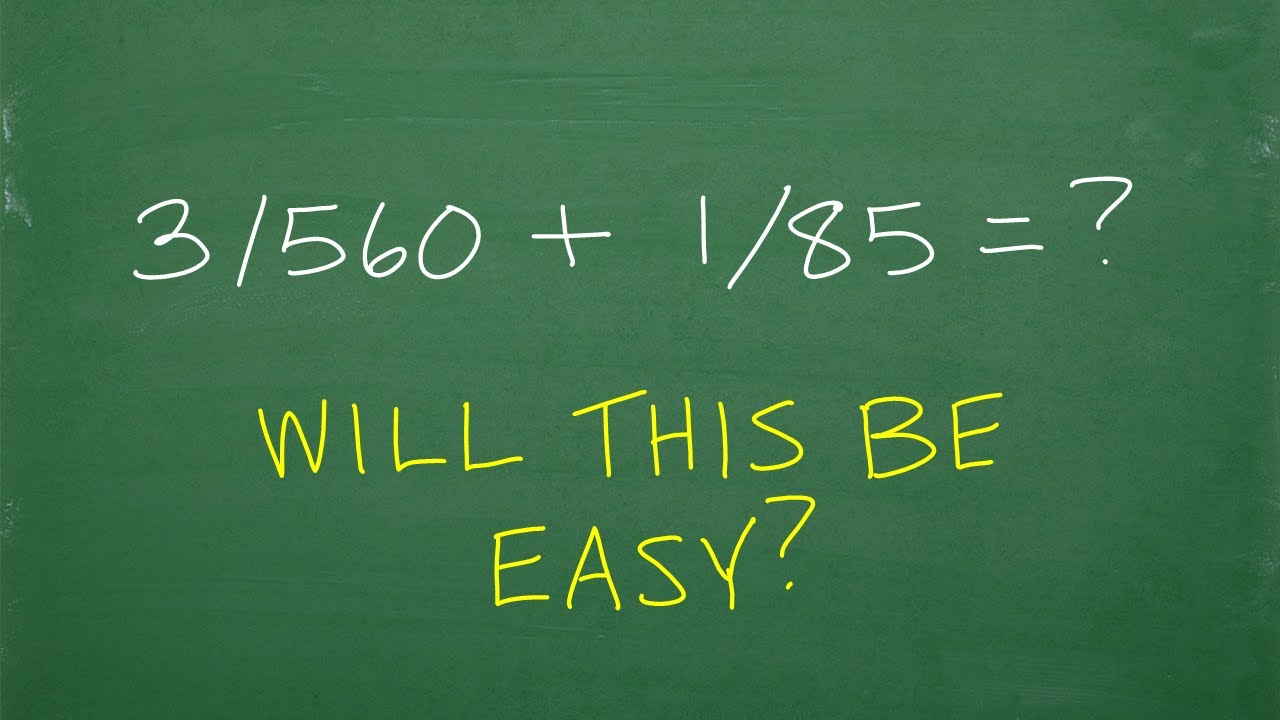(understand this) My Approach to Simplify complex fractions
TLDRThis video script offers a methodical approach to simplifying complex fractions with multiple denominators. It emphasizes the importance of finding the least common denominator (LCD) and multiplying the denominators when factors are not easily identifiable. The script illustrates the process of multiplying everything by the LCD, simplifying the fraction, and identifying restricted values that make the denominator zero. It also hints at a future tip for simplifying complex fractions more efficiently.
Takeaways
- 🔍 The process of simplifying a complex fraction involves eliminating multiple denominators to achieve a simpler expression.
- 🔢 Multiplying by the least common denominator (LCD) or the product of the denominators is a common method to simplify fractions.
- 📚 In cases where the denominators are numbers like 2 and 3, the LCD is the product of the two numbers, which is 6.
- 🎓 Students often find adding fractions challenging due to the need to find a common denominator.
- 🤔 When dealing with expressions like 'X + 2' and 'X + 3', it's not straightforward to find a common denominator, so multiplying the denominators is a practical approach.
- 📉 The least common denominator is not always the product of the denominators; it can sometimes be a smaller number that both denominators divide into evenly.
- 📝 Factoring the denominators can help identify common factors and potentially simplify the expression without multiplying all terms.
- 📚 For more complex expressions, like binomials or polynomials, factoring the denominators might reveal common factors that can simplify the process.
- 📉 When the denominators are prime or have no common factors, the least common multiple (LCM) is the product of the two denominators.
- 📝 After multiplying through by the LCM, simplify the expression by canceling out common factors in the numerator and denominator.
- ⚠️ It's important to identify restricted values that would make the denominator zero, as these are values the variable cannot take.
Q & A
What is a complex fraction?
-A complex fraction is a fraction that has another fraction in its numerator, denominator, or both.
Why is it necessary to simplify complex fractions?
-Simplifying complex fractions is necessary to make the expression easier to understand and work with, and to express the value in its simplest form.
What is the first step in simplifying a complex fraction according to the video?
-The first step is to identify if there are any common factors between the denominators that can be used to simplify the fraction.
What does the video suggest as a quick method to find a common denominator for fractions with different denominators?
-The video suggests multiplying the two denominators as a quick method to find a common denominator.
What is the least common denominator (LCD) and why is it important in simplifying fractions?
-The least common denominator is the smallest number that can be evenly divided by all the denominators in a set of fractions. It is important because it allows you to combine fractions into a single fraction with a common denominator.
Why might you not always want to multiply the denominators to find a common denominator?
-You might not want to multiply the denominators if there is a smaller common denominator that they share, or if the denominators are polynomials that can be factored to reveal a common factor.
What is the purpose of multiplying everything by the least common multiple (LCM) of the denominators in the video's example?
-Multiplying everything by the LCM of the denominators is done to eliminate the fractions and simplify the complex fraction to a single, simpler fraction.
How does the video suggest handling complex fractions with variables in the denominators?
-The video suggests identifying the least common multiple of the variables and constants in the denominators and multiplying the entire expression by this LCM to simplify the complex fraction.
What is the final step in simplifying a complex fraction after multiplying by the LCM?
-The final step is to simplify the resulting expression by canceling out common factors in the numerator and denominator.
Why is it important to identify restricted values after simplifying a fraction?
-Identifying restricted values, such as values that make the denominator zero, is important because these values are not allowed in the original fraction, as they would make the expression undefined.
Outlines
🧩 Simplifying Complex Fractions: Understanding the Approach
This paragraph introduces the process of simplifying complex fractions, which involves dealing with multiple denominators and numerators. The speaker explains the importance of finding a common denominator or a number that can evenly divide the denominators to simplify the fractions. The approach of multiplying the denominators to find the least common denominator (LCD) is discussed, along with the idea of simplifying by multiplying everything by the LCD. The paragraph also touches on the complexity of dealing with expressions like 'X plus two' and 'X plus three', where factors are not easily identifiable, and emphasizes the practice of multiplying denominators as a way to simplify such expressions.
🚫 Identifying Restricted Values in Fractions
The second paragraph focuses on identifying the values that would make the denominator of a fraction equal to zero, which are considered restricted values. The speaker instructs to set the denominator in factor form equal to zero to find these values. In the context of the previous discussion, the restricted values for the given example are identified as 'x cannot equal negative 20 or zero'. The paragraph concludes with a teaser for the next video, where the speaker promises to provide a tip for simplifying complex fractions, and ends with a sign-off.
Mindmap
Keywords
💡Complex Fraction
💡Denominator
💡Numerator
💡Least Common Denominator (LCD)
💡Simplify
💡Multiplying Denominators
💡Factors
💡Common Denominator
💡Restricting Values
💡Simplification Process
💡Variable
Highlights
Simplifying complex fractions involves understanding the approach of eliminating extra fractions.
The easiest way to get rid of a fraction is by finding a number or expression that the denominator evenly divides into.
Multiplying everything by the denominators, such as 5 or X, can simplify the process.
Understanding the concept of common denominators is crucial for adding fractions.
Finding the least common denominator (LCD) is the smallest number that can evenly divide the given denominators.
Multiplying the two denominators is a quick approach to finding a common denominator.
12 is not the least common denominator; 6 is, as it can divide both 2 and 3.
When dealing with expressions like X + 2 and X + 3, multiplying the denominators is a practical approach.
Factoring the denominators can reveal common factors and simplify the process.
If denominators cannot be simplified, multiply them to find the least common multiple (LCM).
Identifying the LCM as the product of the two factors is key when no common factors exist.
Multiplying everything by 5X is a method to simplify the complex fraction when dealing with 5 and X as denominators.
Rewriting the expression with the LCM helps in visualizing the simplification process.
Simplifying the numerator and denominator by canceling out common factors is an essential step.
Factoring out common terms in the numerator can lead to further simplification.
Understanding the restricted values that make the denominator equal to zero is important for the validity of the fraction.
The video promises to provide the best tip for simplifying complex fractions in the next installment.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: