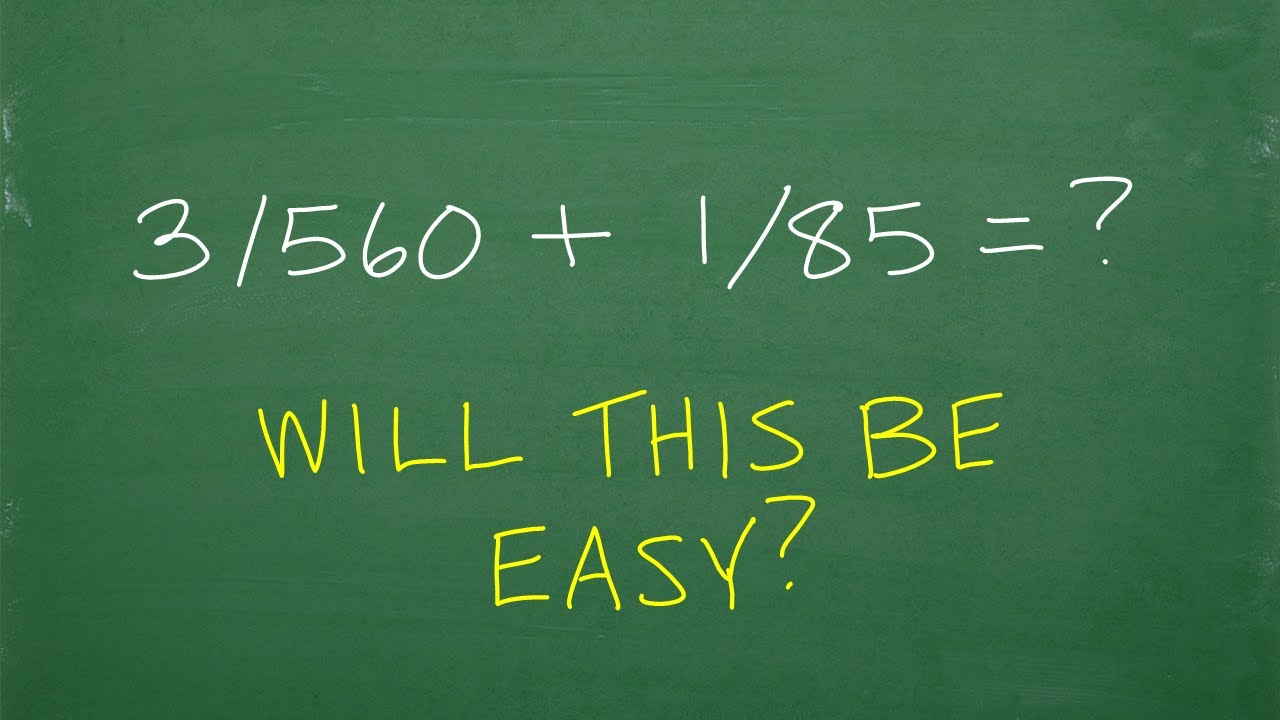Math Antics - Common Denominator LCD
TLDRThis video tutorial introduces the concept of finding the 'Least Common Denominator' (LCD) for adding unlike fractions. It explains the method of identifying the smallest common multiple of two denominators and demonstrates how to convert fractions to equivalent forms with this common denominator. The process is illustrated with examples, such as adding 3/8 and 5/24, and 2/9 with 7/12, to simplify the understanding of the concept. The video emphasizes the importance of practice in mastering the technique.
Takeaways
- 😀 The 'easiest common denominator' method is preferred for its simplicity and quickness.
- 🔍 There are two cases where finding the 'least common denominator' (LCD) is more suitable: when one denominator is a multiple of the other, and when required by a teacher.
- 📚 The LCD method uses the smallest common denominator instead of the product of the denominators.
- 🔢 To find the LCD, determine the least common multiple (LCM) of the two denominators by listing their multiples.
- 📝 A 'multiple' is the result of multiplying a number by another whole number.
- 📋 Organize multiples in a table to find the LCM easily.
- 🤔 Stop listing multiples once a common value is found for both denominators; this is the LCM.
- 📉 Once the LCM is identified, it becomes the new common denominator.
- 📈 Use the numbers that resulted in the LCM to determine the 'whole fractions' needed to convert the original fractions to equivalent fractions with the common denominator.
- 📌 For example, if 4 is the multiplier for the first fraction, use '4/4' as the whole fraction.
- 📑 The provided examples demonstrate the process of finding the LCD for fractions 3/8 + 5/24 and 2/9 + 7/12.
- 📝 The method involves multiplying the numerators and denominators by the appropriate whole fractions to achieve equivalent fractions with the common denominator.
- 📚 Practice is emphasized as a key to learning math effectively.
Q & A
What is the 'easiest common denominator' mentioned in the video?
-The 'easiest common denominator' refers to using the product of the bottom numbers (denominators) of two fractions as the common denominator when adding or comparing fractions.
Why might someone prefer using the 'easiest common denominator' method?
-It is preferred because it is quick and easy to remember, making it a convenient method for finding a common denominator when adding or comparing fractions.
Under what circumstances should you consider using a different method to find a common denominator?
-You should consider using a different method when one fraction's denominator is a multiple of the other's, or when instructed to do so by a teacher.
What is the 'least common denominator' (LCD) and why is it used?
-The 'least common denominator' is the smallest common multiple of the denominators of two fractions. It is used to simplify the process of converting unlike fractions to like fractions without unnecessarily large numbers.
How do you find the least common denominator of two fractions?
-To find the LCD, you list multiples of the denominators and find the smallest number that appears in both lists, which is the least common multiple (LCM) of the two denominators.
What is a 'multiple' in the context of the video?
-A 'multiple' is the result of multiplying a number by another whole number, such as 1, 2, 3, etc.
How does arranging multiples in a table help in finding the LCD?
-Arranging multiples in a table helps to keep track of the multiples for each denominator in an organized manner, making it easier to identify the least common multiple.
What is meant by 'whole fractions' in the context of converting unlike fractions to like fractions?
-'Whole fractions' refer to fractions like 1/1, 2/2, 3/3, etc., which are used to multiply the original fractions to achieve an equivalent fraction with the common denominator.
Can you provide an example of how to find the 'whole fraction' needed for a given fraction?
-Yes, if you need to convert 3/8 to have a common denominator with another fraction and you find that multiplying 8 by 3 gives you the LCM, you would use the 'whole fraction' 3/3 to multiply the original fraction (3/8 * 3/3).
How does the video demonstrate the process of finding the least common denominator and adding fractions?
-The video provides step-by-step examples, such as adding 3/8 and 5/24, where it shows how to find the multiples, identify the LCM, determine the 'whole fractions', and then convert the original fractions to equivalent fractions with the common denominator before adding them.
What is the significance of finding the least common multiple (LCM) in the process of adding fractions?
-The LCM is significant because it serves as the common denominator for the fractions being added. By converting the fractions to equivalent fractions with this common denominator, you can directly add or subtract the numerators while keeping the denominator constant.
Why is it beneficial to use the least common multiple instead of the product of the denominators?
-Using the least common multiple instead of the product of the denominators reduces the size of the numbers involved, making the calculations simpler and less prone to error.
What is the final step in adding fractions once you have found the least common denominator?
-The final step is to add the numerators of the equivalent fractions with the common denominator and keep the common denominator as the new fraction's denominator.
How does the video encourage viewers to practice the skill of finding the least common denominator?
-The video encourages viewers to practice by reminding them to do the exercises for the video, emphasizing that the way to really learn math is through doing the problems.
Outlines
📚 Finding the Least Common Denominator (LCD)
This paragraph introduces a method for converting unlike fractions into like fractions using the 'least common denominator' (LCD), which is a more efficient approach in certain situations. The LCD is the smallest common multiple of the denominators. The process involves listing multiples of the denominators until a common multiple is found, which becomes the new common denominator. The 'whole fractions' required to adjust the original fractions are also determined by the multiples that resulted in the common multiple. The paragraph provides a step-by-step example using the fractions 3/8 and 5/24, demonstrating how to find the LCD and adjust the fractions accordingly.
📘 Least Common Denominator Method Application
The second paragraph continues the discussion on the LCD method, emphasizing its simplicity once understood. It encourages practice through exercises to solidify the learning of the concept. The paragraph also provides a second example using the fractions 2/9 and 7/12, showing how to identify the least common multiple of the denominators, adjust the fractions to have this common denominator, and then add the fractions together. The summary concludes with a reminder to visit www.mathantics.com for more information and ends with a note of encouragement for the viewer's mathematical journey.
Mindmap
Keywords
💡Easiest Common Denominator
💡Unlike Fractions
💡Least Common Denominator (LCD)
💡Multiples
💡Least Common Multiple (LCM)
💡Whole Fractions
💡Denominator
💡Numerator
💡Addition of Fractions
💡Mathematics Exercises
Highlights
Introduction to the concept of finding the 'easiest common denominator' for adding fractions.
Preference for a quick and easy method of finding a common denominator.
Two cases where a different method is better for converting 'unlike' fractions into 'like' fractions.
Explanation of the first case involving multiples of the bottom numbers in fractions.
The second case is when a teacher mandates the use of a different method.
Introduction of the 'least common denominator' method.
The least common denominator involves finding the smallest common multiple of the bottom numbers.
Definition and explanation of a 'multiple' of a number.
Step-by-step guide to finding the Least Common Denominator (LCD).
Creating a table of multiples to organize and identify common multiples.
Using the least common multiple as the new common denominator.
Determining whole fractions to multiply unlike fractions to achieve the common denominator.
Example problem: Adding 3/8 and 5/24 using the least common denominator method.
Demonstration of finding multiples and identifying the least common multiple for 8 and 24.
Using whole fractions 3/3 and 1/1 to adjust fractions to the common denominator of 24.
Multiplication of fractions to achieve 'like' fractions for addition.
Another example problem: Finding the LCD for 2/9 and 7/12.
Finding the least common multiple of 9 and 12, which is 36.
Using whole fractions 4/4 and 3/3 to adjust fractions to the common denominator of 36.
Final addition of the adjusted fractions to demonstrate the least common denominator method.
Encouragement to practice the method through exercises for better understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: