Multivariable chain rule intuition
TLDRThis video script delves into the multi-variable chain rule, offering an intuitive understanding of its concept. The presenter explains the rule by visualizing a multi-variable function in a two-dimensional space, mapping it to a real number line. The script explores the derivative's meaning as a ratio of change, using the Leibniz notation as a mnemonic for the formal argument. It breaks down the total change in the function 'f' into components caused by 'dx' and 'dy', resulting from a 'dt' nudge, and concludes with the chain rule formula, illustrating how these components combine to represent the overall change in 'f'.
Takeaways
- 📚 The multi-variable chain rule is introduced as a concept to understand how changes in multiple variables affect a function.
- 🤔 The video aims to provide an intuitive understanding of why the multi-variable chain rule works, rather than a formal mathematical proof.
- 📈 The script uses the analogy of a two-dimensional space (xy-plane) being mapped to a real number line to explain the function's output.
- 🔍 It discusses how separate functions x(t) and y(t) take a single input t and map it to the xy-plane, which then affects the output of the function f.
- 📉 The concept of a derivative is explored, explaining it as a 'tiny change' or 'nudge' in the input that results in a change in the output.
- 📝 The script breaks down the change in the function's output (f) into components dx and dy, which are the changes in x and y directions respectively.
- 🔄 It explains that dx and dy are not arbitrary but are caused by a change in t (dt), which is the derivative of x and y with respect to t.
- 📐 The Leibniz notation for derivatives is highlighted as a helpful mnemonic and a precursor to a formal argument for the chain rule.
- 🔍 The partial derivatives ∂f/∂x and ∂f/∂y are described as the ratios that show how a tiny nudge in x or y affects the output of f.
- 🧩 The total change in f is the sum of the changes caused by dx and dy, which are in turn caused by dt through the derivatives of x and y with respect to t.
- 🔑 The multi-variable chain rule is presented as a way to combine these individual changes into the overall derivative of f with respect to t.
Q & A
What is the multi-variable chain rule discussed in the video?
-The multi-variable chain rule is a mathematical concept that allows for the differentiation of a function of multiple variables with respect to a single variable, often thought of as a parameter. It's a generalization of the single-variable chain rule to functions of several variables.
How does the video explain the intuition behind the multi-variable chain rule?
-The video uses the analogy of a two-dimensional space being mapped onto a real number line, with the function f(x, y) taking inputs from the xy plane and outputting a real number. It then introduces the idea of thinking about the derivative in terms of 'nudges' in the parameter t, and how these nudges affect the x and y components, and ultimately the output f.
What is the significance of the parameter t in the context of the multi-variable chain rule?
-In the script, t is used as a single variable that influences both x and y, which in turn affect the output of the function f. The changes in x and y due to a change in t are central to understanding how the multi-variable chain rule breaks down the total derivative of f with respect to t.
How does the video script describe the relationship between a small change in t and the resulting changes in x and y?
-The script describes this relationship by stating that a small change in t (dt) causes a change in x (dx) and y (dy), with these changes being proportional to dt. The derivatives dx/dt and dy/dt represent the rates of change of x and y with respect to t.
What is the meaning of the partial derivatives in the context of the multi-variable chain rule?
-The partial derivatives in the multi-variable chain rule, ∂f/∂x and ∂f/∂y, represent the rate of change of the function f with respect to x and y, respectively, while holding the other variable constant. They are used to determine the contribution of each variable to the total change in f.
How does the script explain the concept of 'nudging' in the context of derivatives?
-The script uses the term 'nudging' to describe a small change or increment in the variables or parameters. It explains that the derivative of a function at a point can be thought of as the ratio of the change in the function's output to the 'nudge' in its input variables.
What is the role of Leibniz notation in the explanation provided by the video script?
-Leibniz notation, which uses the fractional form (e.g., dx/dt), is highlighted as a helpful mnemonic and a visual representation of the ratio that the derivative represents. It is used to illustrate the relationship between the change in the function's output and the change in its inputs.
How does the video script connect the partial derivatives to the changes in the function's output due to changes in x and y?
-The script connects the partial derivatives to the changes in the function's output by multiplying the partial derivatives with the corresponding changes in x and y (dx and dy). This shows how each component of the change in the function's output is related to the changes in its variables.
What is the final expression derived in the video script that represents the multi-variable chain rule?
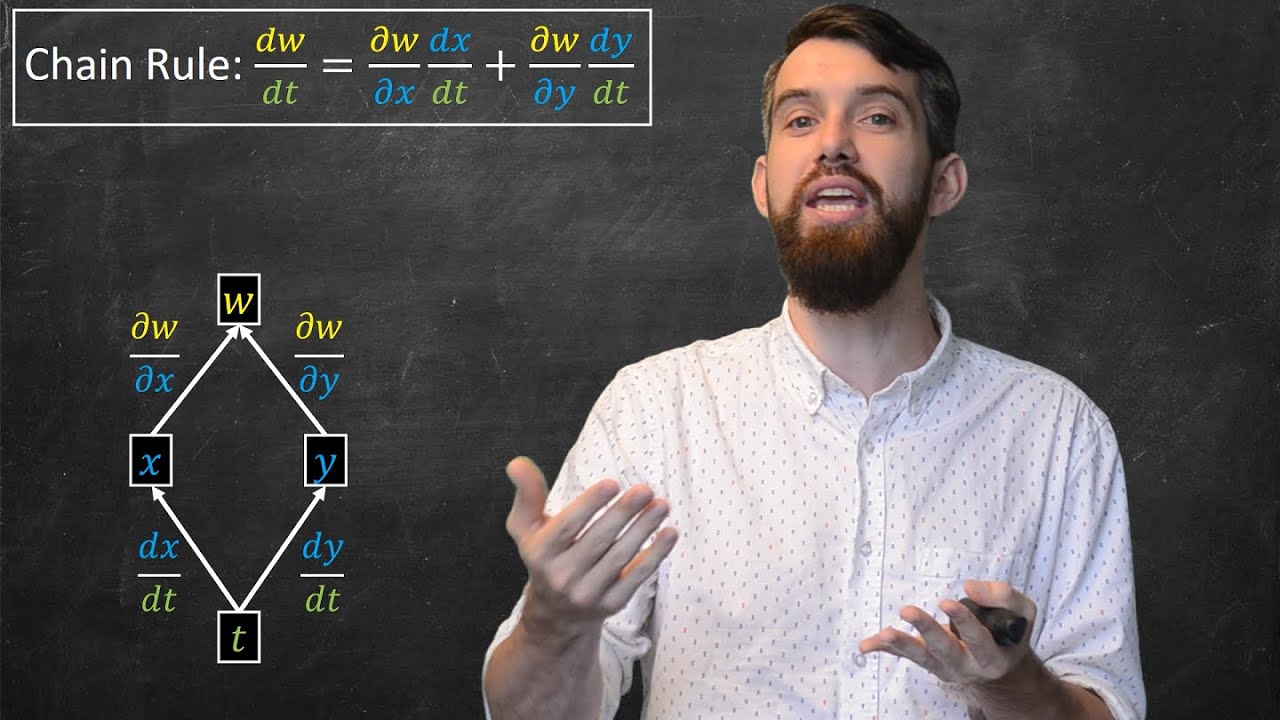
-The final expression derived in the script is the multi-variable chain rule itself, which is df/dt = (∂f/∂x)(dx/dt) + (∂f/∂y)(dy/dt). This expression shows how the total derivative of f with respect to t can be found by summing the effects of the changes in x and y on f.
Why does the video script emphasize the importance of understanding the intuition behind the multi-variable chain rule?
-The script emphasizes the importance of intuition to provide a conceptual understanding that can serve as a foundation for more formal mathematical arguments. It helps in visualizing the process and understanding why the multi-variable chain rule works the way it does.
What does the video script suggest about the relationship between the single-variable and multi-variable chain rules?
-The script suggests that the multi-variable chain rule is a natural extension of the single-variable chain rule to functions with multiple inputs. It retains the core concept of relating the rate of change of the output to the rates of change of the inputs.
Outlines
📚 Introduction to the Multi-Variable Chain Rule
In this paragraph, the voiceover introduces the concept of the multi-variable chain rule, explaining its importance and setting up the intuition behind it. The function f(x, y) is described as mapping a two-dimensional space to a real number line, with x(t) and y(t) being functions of t. The explanation includes how changes in t affect x and y, ultimately impacting f.
🔄 Understanding Changes in Variables
This section dives into how small changes in t, represented as dt, translate into changes in x and y, and subsequently in the function f. It emphasizes the proportionality between these changes and how derivatives dx/dt and dy/dt capture these relationships. The explanation uses the idea of 'nudging' t to illustrate how tiny changes propagate through the functions.
📐 Derivatives and Partial Derivatives
Here, the focus shifts to understanding how partial derivatives reflect changes in the output of f due to changes in x and y. The voiceover explains that the partial derivative with respect to x indicates how a small change in x affects f, and similarly for y. The concept of treating these derivatives as fractions is discussed as a useful mnemonic and a scaffold for more formal mathematical arguments.
🧩 Composing Changes to Understand Total Change in f
This paragraph brings together the ideas of partial derivatives and their contributions to the total change in f. It explains how changes in x and y, driven by changes in t, combine to affect f. The multi-variable chain rule is derived by adding the effects of changes in x and y, both of which are functions of t. The explanation highlights the intuition behind the formula and its components.
Mindmap
Keywords
💡Multi-variable chain rule
💡Two-dimensional space
💡Derivative
💡Partial derivative
💡Differential properties
💡Leibniz notation
💡Nudge
💡Ratio
💡Composite function
💡Intuition
💡Formal argument
Highlights
Introduction to multi-variable chain rule with a focus on understanding the underlying intuition.
Explaining the concept of a multi-variable function f(x, y) in a two-dimensional space.
Mapping the two-dimensional space to a real number line as the output of the function.
Introducing the idea of x(t) and y(t) as functions of a single variable t.
Describing the derivative as a measure of the change in the function's output due to a small change in the input.
Using the concept of 'nudging' to illustrate the effect of a small change in t on the xy plane.
Breaking down the change in the function's output into components dx and dy.
Explaining the role of the derivative in determining how a change in t affects x and y.
The significance of the Leibniz notation in representing the ratio of changes in variables.
The formal argument for the chain rule will be discussed in a subsequent video.
The partial derivative as a measure of the change in the output due to a nudge in a specific variable.
Describing the total change in f as a combination of changes caused by both x and y.
The chain rule as a method to calculate the total derivative by considering the individual contributions of x and y.
The cancellation of partial derivatives with dx and dy in the chain rule formula.
The final expression of the multi-variable chain rule, providing a clear understanding of how changes in x and y affect the output.
The importance of understanding the individual contributions to the change in f for a deeper comprehension of the chain rule.
Transcripts
Browse More Related Video
The Multi-Variable Chain Rule: Derivatives of Compositions

Multivariable chain rule and directional derivatives

Vector form of the multivariable chain rule

Introduction to 3d graphs | Multivariable calculus | Khan Academy

Directional derivative, formal definition

Business Calculus - Math 1329 - Section 2.4 - Chain Rule
5.0 / 5 (0 votes)
Thanks for rating: