Business Calculus - Math 1329 - Section 2.4 - Chain Rule
TLDRThis video script delves into the concept of the chain rule in calculus, a fundamental principle for differentiating composite functions. The chain rule states that the derivative of a composite function is the product of the derivative of the outer function and the derivative of the inner function. The script provides a clear explanation and several examples to illustrate the application of the chain rule, including raising a function to a power, finding the derivative of a square root function, and calculating the rate of change of a function with respect to time. The video also touches on the Leibniz notation for derivatives, offering an alternative perspective on the chain rule. The examples range from basic functions to more complex scenarios, such as calculating the rate of change of a company's gross earnings or the total cost of manufacturing units over time. The script is an excellent resource for those looking to understand and apply the chain rule in various mathematical contexts.
Takeaways
- 📚 The Chain Rule is essential for finding derivatives of composite functions, where one function is nested within another.
- 🔢 The formula for the Chain Rule is expressed as ( p'(x) = f'(g(x)) \cdot g'(x) ), where ( f ) is the outer function and ( g ) is the inner function.
- 📈 To apply the Chain Rule, first identify the outer and inner functions, then find their respective derivatives.
- 💡 The Chain Rule can be thought of as bringing down the power from the outer function, keeping the inner function the same, and multiplying by its derivative.
- 📌 Examples are used to illustrate the process of finding derivatives using the Chain Rule, including simplifying expressions and applying the rule to more complex functions.
- 🤔 The Chain Rule is not only for complex functions but also implicitly used in simpler functions, like ( f(x) = x^6 ), where the derivative is ( 6x^5 ).
- 🔧 The Chain Rule can be extended for functions composed of multiple layers, where you continue to apply the rule until you reach a basic function.
- 📐 The concept of a tangent line to a function at a specific point involves finding both the slope (derivative) and the point on the function.
- 💹 The Chain Rule is also applicable in real-world scenarios, such as calculating the rate of change of a company's gross earnings over time.
- ✅ The Leibniz notation for derivatives can be used as an alternative method to represent the Chain Rule, where ( \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} ).
- 🤓 Memorizing the derivatives of common functions, like the power rule and the derivative of the square root function, is crucial for efficiently applying the Chain Rule.
Q & A
What is the Chain Rule in calculus?
-The Chain Rule is a fundamental theorem used for finding the derivative of composite functions. It states that the derivative of a function composed of two functions is the product of the derivative of the outer function evaluated at the inner function and the derivative of the inner function.
How do you apply the Chain Rule to the function p(x) = (x^2 + 4x + 5)^7?
-To apply the Chain Rule here, you identify the outer function f(x) as x^7 and the inner function g(x) as x^2 + 4x + 5. The derivative p'(x) is then f'(g(x)) * g'(x), which translates to 7(x^2 + 4x + 5)^6 * (2x + 4).
What is the derivative of the square root of 6x - 7 using the Chain Rule?
-The outer function is the square root, which has a derivative of 1/(2√x). The inner function is 6x - 7, with a derivative of 6. Applying the Chain Rule, the derivative is (1/2√(6x - 7)) * 6.
How do you find the equation of the tangent line to the function p(x) = (9x - 1)^(1/3) at x = 1?
-First, find the derivative p'(x) which is (1/3)(9x - 1)^(-2/3) * 9. Then evaluate p'(1) to find the slope of the tangent line. Next, find the value of p(1) to get the point on the function. Finally, use the slope-point form of a line to write the equation of the tangent line.
What is the gross earnings for the year 2018, given the function f(t) = √(12t^2 + 6t + 300)?
-To find the gross earnings for the year 2018, substitute t = 2 (since 2018 is two years after 2016) into the function f(t). The result is f(2) = √(12(2)^2 + 6(2) + 300), which equals 22.45 million dollars.
How do you find the rate at which the gross earnings are changing in 2018 for the given function?
-First, find the derivative of the function f(t) with respect to t, which represents the rate of change. Then, evaluate this derivative at t = 2 to find the rate of change of gross earnings in 2018.
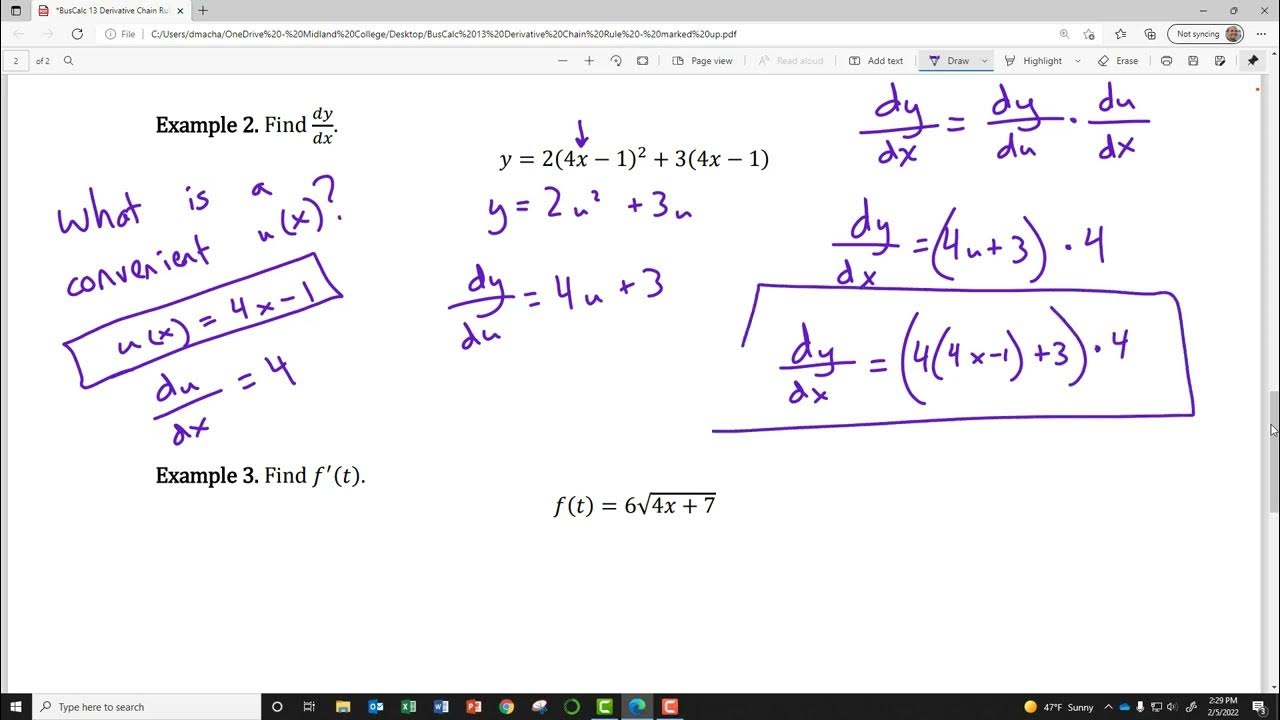
What is the Leibniz notation for derivatives and how is it used in the Chain Rule?
-The Leibniz notation for derivatives is a way to express the derivative of a composite function as a fraction: dy/dx = (dy/du) * (du/dx). It is used in the Chain Rule to find the derivative of a function of a function by canceling out the intermediate variable.
How do you use the Leibniz notation to find the derivative dy/dx if y = u^7 + 3u and u = 2x^2 + 5?
-First, find dy/du by differentiating y with respect to u. Then, find du/dx by differentiating u with respect to x. Finally, substitute the expression for u in terms of x into dy/du * du/dx to express the derivative entirely in terms of x.
What is the rate at which the total cost is changing with respect to time three hours after production begins, given the functions c(x) = 0.5x^2 + 4x + 1200 and x(t) = t^2 + 80t?
-Apply the Chain Rule by finding dc/dx and then using the relationship x(t) to find dx/dt. The rate of change of the total cost with respect to time is then found by substituting t = 3 into the expression (dc/dx) * (dx/dt).
What is the derivative of a function of the form f(x) = x^n, where n is a constant, according to the Power Rule?
-According to the Power Rule, the derivative of f(x) = x^n is f'(x) = n * x^(n-1).
How can you simplify the derivative expression 7(x^2 + 4x + 5)^6 * (2x + 4)?
-You can simplify by distributing the 7 across the terms in the parentheses and then combining like terms. The result is 14x * (x^2 + 4x + 5)^6 + 28 * (x^2 + 4x + 5)^6.
Outlines
📚 Introduction to the Chain Rule
This paragraph introduces the concept of the chain rule in calculus, which is essential for finding derivatives of composite functions. It explains that the chain rule is used when a function, denoted as p(x), is composed of an outer function (f) acting on an inner function (g(x)). The paragraph provides an example, where p(x) is (x^2 + 4x + 5)^7, and walks through the process of finding its derivative using the chain rule formula: p'(x) = f'(g(x)) * g'(x). It also demonstrates a shortcut method for applying the chain rule, especially useful when dealing with power functions.
🔢 Applying the Chain Rule to Various Functions
The second paragraph delves into applying the chain rule to different types of functions. It covers examples involving square roots, cube roots, and quotients, demonstrating how to find the derivatives of these functions using the chain rule. The paragraph emphasizes the importance of understanding the structure of composite functions and the order in which operations are performed. It also touches on the concept of chaining derivatives together, where multiple layers of functions are nested within each other, and the chain rule is applied iteratively to find the derivative.
📈 Tangent Line and Rate of Change Calculations
This paragraph discusses the application of the chain rule in finding the equation of a tangent line to a given function at a specific point, as well as calculating the rate of change of a function. It provides a step-by-step guide to finding the slope of the tangent line by evaluating the derivative at the point of tangency. The paragraph also covers how to compute the gross earnings of a company over time and how to determine the rate at which these earnings are changing, using the chain rule to find derivatives with respect to time.
🧮 Leibniz Notation and Expanded Chain Rule
The fourth paragraph introduces the Leibniz notation for derivatives, which is an alternative way to express the chain rule. It explains that this notation allows for a more direct calculation of how a function y changes with respect to an independent variable x, even when y is composed of intermediate variables like u. The paragraph provides an algebraic example where y is a function of u, and u is a function of x, showing how to find the derivative dy/dx using the Leibniz notation. It also emphasizes the conceptual approach to understanding the chain rule through this notation, even though the actual calculation follows the standard rules of differentiation.
🏭 Chain Rule in Cost Analysis
The fifth paragraph presents a complex application of the chain rule in a real-world scenario, specifically in cost analysis for a factory. It discusses how to find the rate at which the total cost of manufacturing is changing with respect to time. The paragraph explains the need to use the chain rule to relate the total cost function to time, given that the cost function is in terms of the number of units produced, which is itself a function of time. It concludes with the calculation of the rate of change of the total cost three hours after production begins.
📊 Final Thoughts and Conclusion
The final paragraph summarizes the key points covered in the video script, emphasizing the importance of the chain rule in calculus and its broad applicability across various mathematical and real-world problems. It also provides a notation for indicating the evaluation of a derivative at a specific point, using a vertical bar with a subscript. The paragraph concludes with a reminder about the units involved in the derivative calculations, ensuring that the final answer is expressed in the correct units, such as dollars per hour in the context of the factory cost analysis.
Mindmap
Keywords
💡Chain Rule
💡Derivative
💡Function
💡Outer Function
💡Inner Function
💡Power Rule
💡Composite Function
💡Tangent Line
💡Rate of Change
💡Quotient Rule
Highlights
Section 2.4 focuses on the chain rule, an essential tool for finding derivatives of composite functions.
The chain rule states that the derivative of a composite function f(g(x)) is f'(g(x)) * g'(x).
The outer function represents the final operation performed, while the inner function is what is being operated on.
Example 1 demonstrates finding the derivative of x^2 + 4x + 5 raised to the 7th power using the chain rule.
The derivative is found by multiplying the derivative of the outer function evaluated at the inner function by the derivative of the inner function.
Example 2 shows finding the derivative of the square root of 6x - 7 using the chain rule.
The derivative of the square root function is 1/(2√x), which is applied to the inner function 6x - 7.
Example 3 involves finding the derivative of (1/(2x - 1))^3 using the chain rule and power rule.
Rewriting the expression with a negative exponent makes applying the chain rule and power rule more straightforward.
Example 4 finds the equation of the tangent line to 9x - 1 raised to the 1/3 power at x = 1.
The slope of the tangent line is found by evaluating the derivative of the function at x = 1.
The point on the function at x = 1 is used to find the y-coordinate of the tangent point.
The equation of the tangent line is found using the slope-intercept form with the slope and point.
Example 5 calculates the gross earnings for a company in 2018 using the given function.
The derivative of the function is found to determine the rate at which earnings are changing in 2018.
The rate of change is evaluated at t = 2 (2018) to find the rate of increase in earnings that year.
The chain rule can be formulated using Leibniz's notation, treating the derivatives like fractions.
Example 6 demonstrates using the chain rule with Leibniz notation to find dy/dx for y = u^7 + 3u where u = 2x^2 + 5.
Substituting the expression for u in terms of x allows finding dy/dx without the intermediate variable u.
Example 7 involves finding the rate at which total cost is changing with respect to time for a factory.
The chain rule is used to express the derivative of cost with respect to time in terms of the production function x(t).
The derivative is evaluated at t = 3 to find the rate of change in cost 3 hours into production.
The units of the rate of change are dollars per hour, indicating how much cost increases per hour of production.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: