2019 Multiple choices 24, 25

MATH MATTERS
15 May 202103:20
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers an in-depth review of the 2019 AP Calculus Multiple Choice exam, meticulously dissecting the questions to provide students with a clear understanding of the concepts tested. It covers a range of topics, from limits and derivatives to integrals and series, with a focus on problem-solving strategies and common pitfalls. The analysis is designed to not only help students prepare for the exam but also to deepen their grasp of calculus, making it an invaluable resource for those looking to excel in their studies.

Takeaways
  • 📘 The 2019 AP Calculus exam includes both AB and BC sections, with distinct sets of multiple-choice questions.
  • 📝 Understanding the fundamental theorem of calculus is crucial for solving many problems.
  • 📐 Graph interpretation is a key skill, especially for questions involving derivatives and integrals.
  • 📈 Pay close attention to the behavior of functions, including limits and continuity.
  • 🔍 Review common differentiation and integration techniques, including the chain rule, product rule, and integration by parts.
  • ⚖️ Be prepared to solve real-world application problems, such as those involving rates of change and areas under curves.
  • 🔢 Mastery of sequences and series, especially for the BC exam, is essential.
  • ⏰ Time management during the exam is critical; practice pacing yourself through each section.
  • 💡 Utilize multiple choice strategies such as process of elimination and plugging in answer choices.
  • 📚 Consistent practice with past exam questions can greatly improve familiarity with the exam format and question types.
Q & A

  • What is the main focus of the 2019 AP Calculus Multiple Choice problems review?

    -The main focus is to analyze and understand the types of questions, strategies for solving them, and the concepts tested in the 2019 AP Calculus Multiple Choice section.

  • What are some common types of questions found in the AP Calculus Multiple Choice section?

    -Common types include limit problems, derivative problems, integral problems, and application-based questions involving rates of change, accumulation, and optimization.

  • How can students prepare for limit problems in the AP Calculus exam?

    -Students should practice using algebraic manipulation, L'Hôpital's Rule, and understanding the behavior of functions as they approach certain values.

  • What is the significance of understanding the concept of limits in calculus?

    -Understanding limits is crucial as they form the foundation for understanding continuity, differentiability, and the behavior of functions at critical points.

  • How can students approach derivative problems in the AP Calculus exam?

    -Students should be familiar with the power rule, product rule, quotient rule, and chain rule, as well as techniques for finding derivatives of trigonometric and exponential functions.

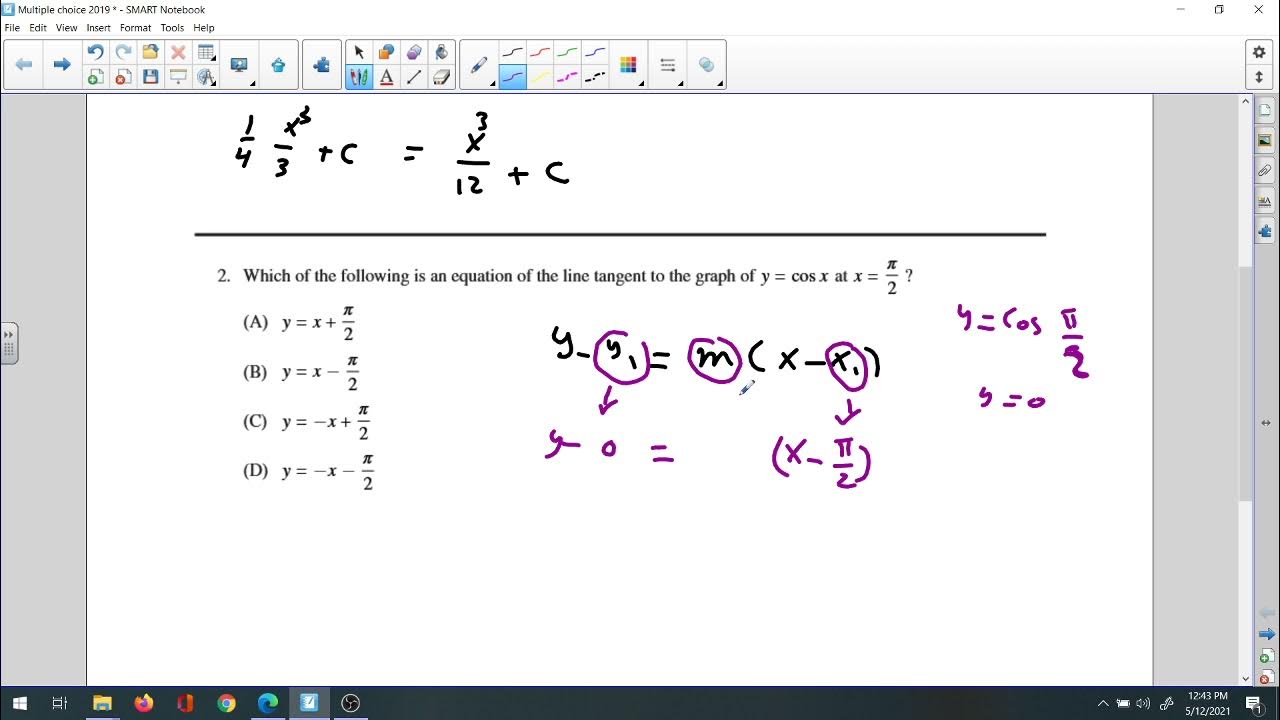
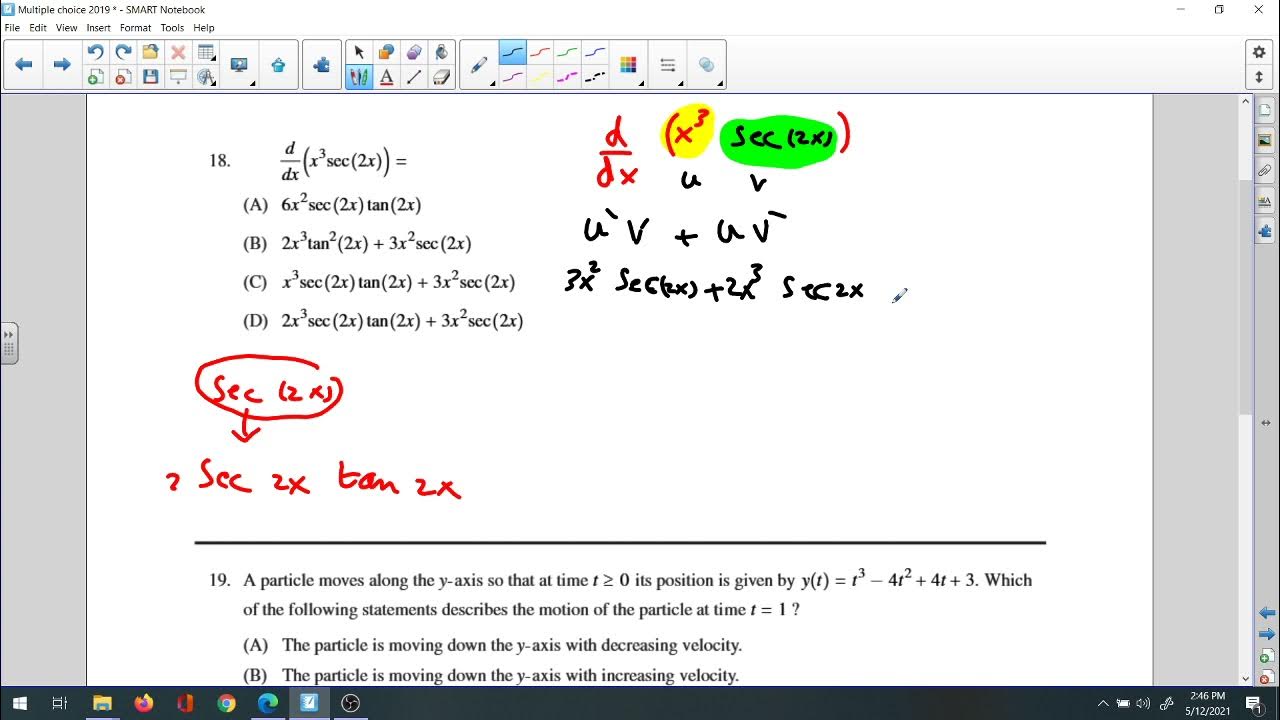
  • What is the product rule in calculus and why is it important?

    -The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. It is important for solving problems involving the rates of change of products of variables.

  • How can integral problems be approached in the AP Calculus exam?

    -Students should be proficient in using substitution, integration by parts, and recognizing standard integrals to solve integral problems efficiently.

  • Why is substitution a useful technique in integration?

    -Substitution simplifies the integral by transforming it into a simpler form that can be more easily evaluated, often by recognizing a pattern or a known integral.

  • What are some strategies for solving application-based questions in the AP Calculus exam?

    -Students should be able to set up equations based on the problem's context, translate word problems into mathematical expressions, and apply appropriate calculus concepts such as optimization or accumulation.

  • How can students improve their problem-solving skills in calculus?

    -Regular practice, understanding the underlying concepts, and learning from mistakes are key strategies. Additionally, reviewing solved examples and discussing problems with peers or teachers can be beneficial.

  • What is the role of optimization problems in the AP Calculus exam?

    -Optimization problems test students' ability to apply calculus to real-world scenarios, such as finding maximum or minimum values of functions, which is crucial in fields like economics, physics, and engineering.

Outlines
00:00
📚 AP Calculus Review

This paragraph introduces the task of reviewing AP Calculus Multiple Choice problems from the year 2019. The focus is on revisiting the problems to understand the concepts and strategies involved in solving them, which is crucial for students preparing for the AP exam.

Mindmap
Keywords
💡Derivative
A derivative represents the rate at which a function is changing at any given point. In calculus, it's the slope of the tangent line to the curve of a function at a specific point. This concept is crucial for solving problems related to instantaneous rates of change and finding local maxima or minima.
💡Integral
An integral is a fundamental concept in calculus that represents the accumulation of quantities, such as areas under a curve. Integrals are used to calculate total values from rates of change and are essential for solving problems involving areas and volumes.
💡Chain Rule
The chain rule is a formula for computing the derivative of the composition of two or more functions. It's essential for dealing with complex functions where one function is nested inside another, allowing the calculation of rates of change in multi-step processes.
💡Product Rule
The product rule is used to find the derivative of the product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. This is vital for differentiating functions that are products of two or more functions.
💡Quotient Rule
The quotient rule is used to find the derivative of a quotient of two functions. It states that the derivative of a quotient is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all over the square of the denominator. This rule is crucial for solving problems involving division of functions.
💡Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus links the concept of differentiation and integration, showing that they are inverse processes. It states that the integral of a function's derivative over an interval gives the change in the function's values over that interval. This theorem is central to understanding the relationship between rates of change and accumulated quantities.
💡Limits
A limit is the value that a function approaches as the input approaches some value. Limits are foundational to calculus, used to define derivatives and integrals, and to deal with problems involving continuity and discontinuities in functions.
💡Continuity
Continuity means that a function has no breaks, jumps, or holes in its domain. A continuous function can be graphed without lifting the pencil from the paper. Understanding continuity is important for analyzing and solving calculus problems involving limits and derivatives.
💡Implicit Differentiation
Implicit differentiation is used to find the derivative of functions that are not explicitly solved for one variable in terms of another. It is particularly useful for dealing with equations where y is defined implicitly as a function of x. This technique is necessary for solving complex problems involving related rates and other applications.
💡Optimization
Optimization involves finding the maximum or minimum values of a function, which is a common application in calculus. It often involves taking the derivative of a function, setting it equal to zero, and solving for critical points. These problems are essential for real-world applications where optimal solutions are required.
Highlights

Introduction to the 2019 AP Calculus exam format and structure.

Explanation of the multiple-choice question types in the exam.

Strategies for tackling rate of change problems.

Analysis of the integration by parts technique.

Discussion on the application of L'Hôpital's Rule in limit problems.

Key concepts in the Fundamental Theorem of Calculus.

Approaches to solving optimization problems in calculus.

The importance of understanding the concept of derivatives.

Review of common mistakes made in the application of the chain rule.

Tips for solving problems involving parametric equations.

Insights into the use of trigonometric identities in calculus problems.

Highlighting the role of sequences and series in calculus.

Exploration of the concept of continuity and its implications.

Discussion on the application of the Mean Value Theorem.

Techniques for solving volume and surface area problems.

The significance of the Riemann Sum in understanding integrals.

Review of the AP Calculus scoring guidelines and how to maximize points.

Final thoughts and advice for students preparing for the AP Calculus exam.

Transcripts

Browse More Related Video

2019 Multiple choices 1,2

2019 Multiple choices 22,23

2019 Multiple choices 76,77,78

2019 Multiple choices 18,19

2019 Multiple choices 3,4

2019 Multiple choices 87,88

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusMultiple ChoiceMath Problems2019 ExamEducationalCollege PrepCritical ThinkingMathematicsAdvanced PlacementExam Review