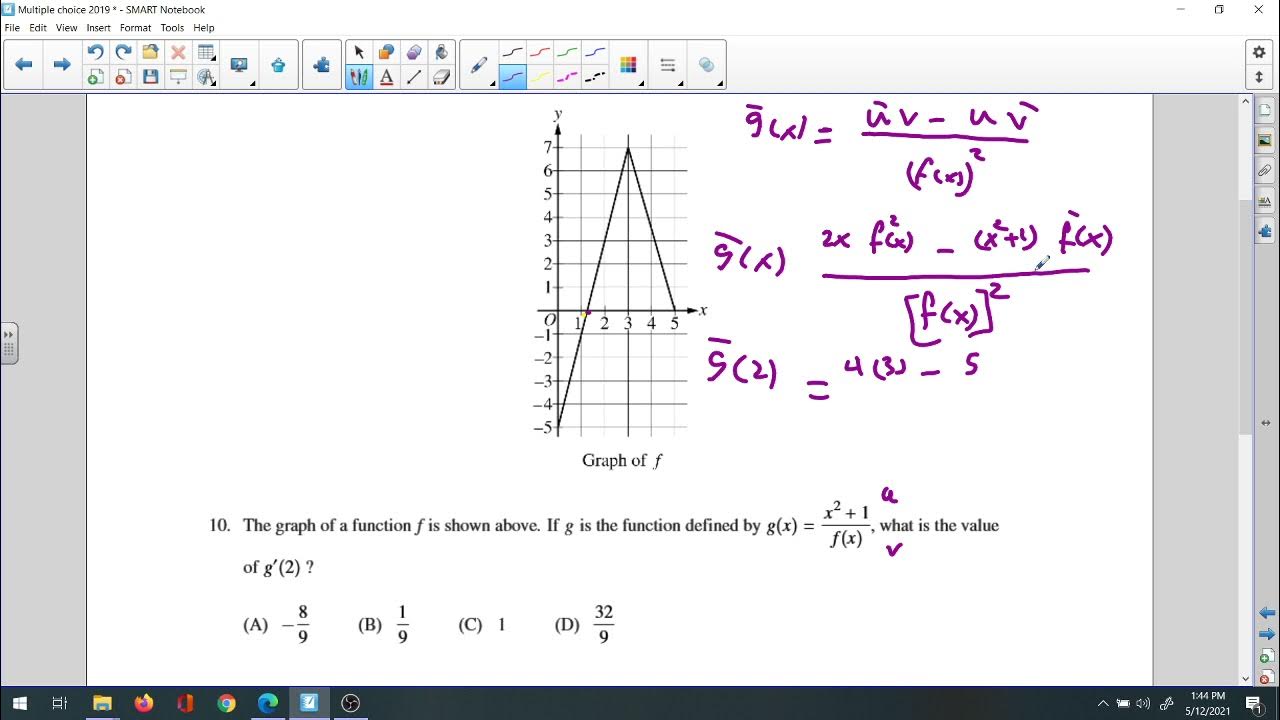
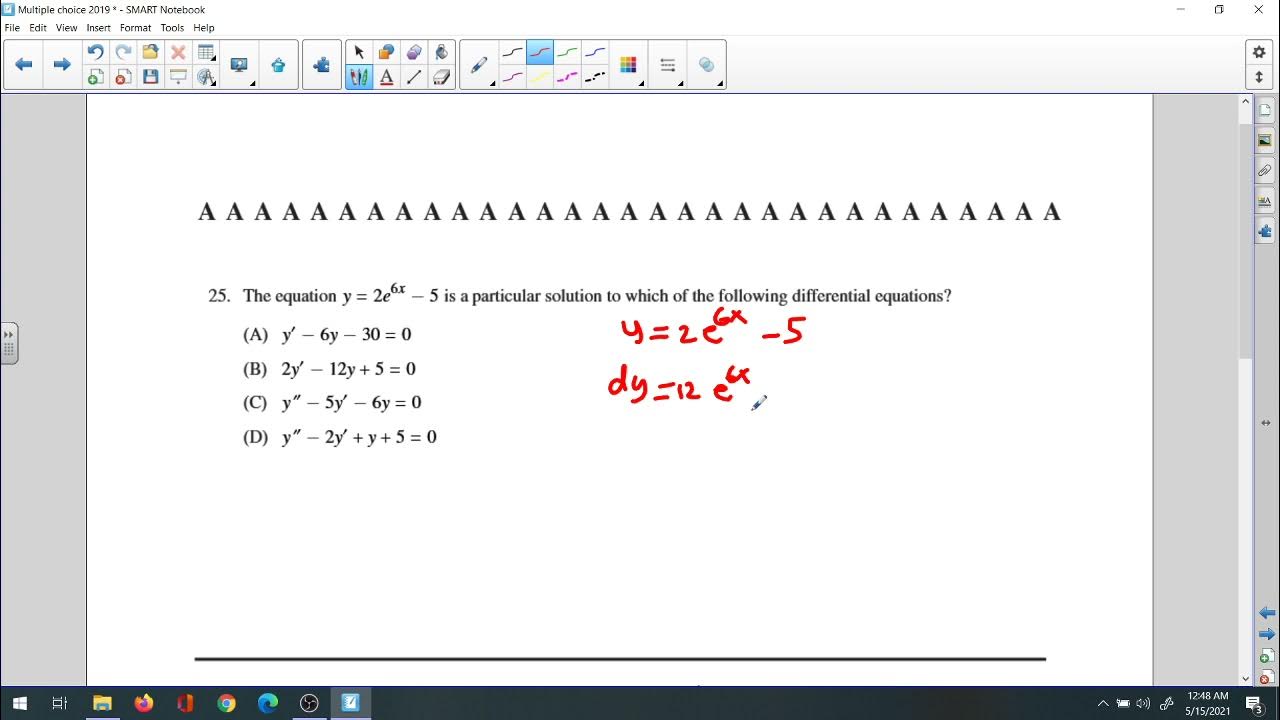
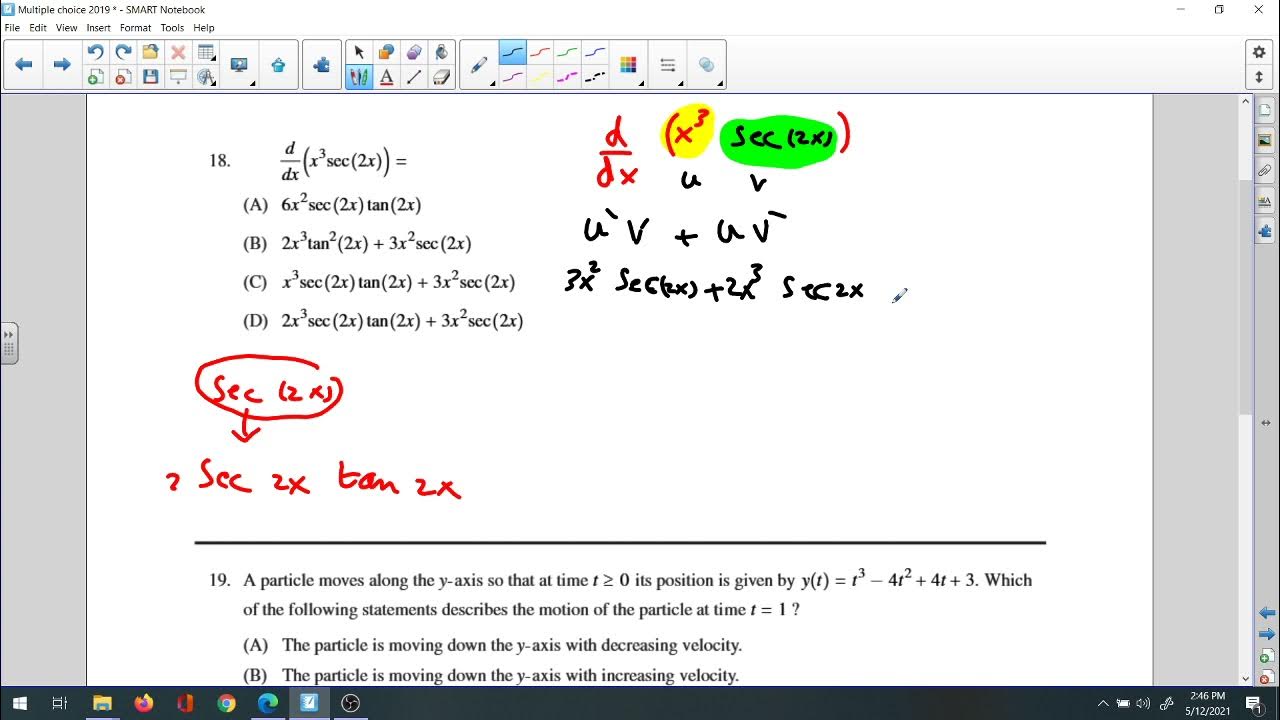
2019 Multiple choices 1,2

MATH MATTERS
15 May 202104:29
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of the 2019 AP Calculus Multiple Choice exam, dissecting the complexity of the problems and providing insights into problem-solving strategies. It aims to engage viewers by highlighting key concepts tested, such as limits, derivatives, and integrals, and by offering tips for tackling the challenging questions that AP Calculus students might face. The summary is designed to pique interest in advanced mathematical concepts and to prepare students for the rigors of the AP exam.

Takeaways
  • 📘 Thorough review of the 2019 AP Calculus Multiple Choice problems.
  • 📊 Emphasis on understanding fundamental calculus concepts.
  • 📝 Detailed breakdown of problem-solving strategies for each question.
  • 📈 Explanation of common mistakes and how to avoid them.
  • 🔍 In-depth analysis of specific problem types, including limits and derivatives.
  • 🎯 Tips for improving speed and accuracy in answering multiple choice questions.
  • 🔄 Importance of practicing with past papers to familiarize with the exam format.
  • 🧮 Step-by-step solutions provided for complex problems.
  • 📚 Resources recommended for further study and practice.
  • 👍 Encouragement to focus on weaker areas and continuously assess progress.
Q & A

  • What topics are primarily covered in the 2019 AP Calculus Multiple Choice problems?

    -The 2019 AP Calculus Multiple Choice problems cover topics such as limits, derivatives, integrals, and the Fundamental Theorem of Calculus.

  • How should students approach limit problems in the AP Calculus exam?

    -Students should evaluate limits using techniques like factoring, rationalizing, and applying L'Hopital's Rule when appropriate.

  • What strategies are recommended for solving derivative problems in the exam?

    -Students should use rules such as the power rule, product rule, quotient rule, and chain rule to find derivatives efficiently.

  • How can integrals be solved in the AP Calculus Multiple Choice section?

    -Integrals can be solved using methods like substitution, integration by parts, and recognizing standard integral forms.

  • What is the significance of the Fundamental Theorem of Calculus in the exam?

    -The Fundamental Theorem of Calculus connects differentiation and integration, allowing students to evaluate definite integrals and understand antiderivatives.

  • What are common mistakes to avoid when solving calculus problems on the AP exam?

    -Common mistakes include algebraic errors, misapplying calculus rules, and not checking work for accuracy.

  • How important is time management during the AP Calculus Multiple Choice section?

    -Time management is crucial; students should pace themselves, prioritize easier problems, and leave time to review their answers.

  • What resources are helpful for preparing for the AP Calculus exam?

    -Helpful resources include review books, online practice exams, instructional videos, and tutoring sessions.

  • How can students improve their problem-solving skills for the AP Calculus exam?

    -Students can improve by practicing a variety of problems, understanding underlying concepts, and seeking help for difficult topics.

  • What mindset should students adopt when approaching the AP Calculus exam?

    -Students should remain calm, stay confident in their preparation, and approach each problem methodically to maximize their performance.

Outlines
00:00
📚 AP Calculus Review 2019

This paragraph focuses on reviewing multiple-choice problems from the 2019 AP Calculus exam. It suggests a need to revisit and analyze the types of questions that were asked, potentially to better understand the exam format and prepare for future tests. The year mentioned indicates a specific time frame for the review, which could be useful for educators and students alike.

Mindmap
Keywords
💡Limits
In calculus, a limit refers to the value that a function approaches as the input approaches some value. Limits are essential for defining derivatives and integrals. For example, in the script, a limit problem might ask what value f(x) approaches as x approaches 2.
💡Derivatives
A derivative represents the rate at which a function is changing at any given point and is a fundamental tool in calculus. It is symbolized as f'(x) or dy/dx. The script might demonstrate finding the derivative of a function such as f(x) = x^2 to illustrate how derivatives measure instantaneous rate of change.
💡Integrals
An integral calculates the area under a curve and is a fundamental concept in calculus. There are definite and indefinite integrals. In the script, solving an integral like ∫ x dx would show how to determine the antiderivative or the area under a curve from one point to another.
💡Fundamental Theorem of Calculus
This theorem links the concept of differentiation and integration, stating that differentiation and integration are inverse processes. The script might include examples demonstrating how to use this theorem to evaluate integrals by finding antiderivatives.
💡Chain Rule
The chain rule is a formula for computing the derivative of the composition of two or more functions. It is written as (f(g(x)))' = f'(g(x)) * g'(x). In the script, this might be used to find the derivative of a composite function such as sin(x^2).
💡Product Rule
The product rule is used to find the derivative of the product of two functions and is stated as (fg)' = f'g + fg'. The script might cover how to apply this rule to functions like x^2 * e^x.
💡Quotient Rule
The quotient rule is used to differentiate the quotient of two functions, given by (f/g)' = (f'g - fg') / g^2. The script may demonstrate its application on problems like (x^2)/(sin(x)).
💡Implicit Differentiation
This technique is used to find derivatives of equations not solved for one variable in terms of the other. The script might use an example such as differentiating x^2 + y^2 = 1 implicitly to find dy/dx.
💡Riemann Sum
A Riemann sum approximates the area under a curve using rectangles. The script might illustrate how to use left, right, and midpoint Riemann sums to estimate the integral of a function over an interval.
💡Critical Points
Critical points are where the derivative of a function is zero or undefined, indicating potential maxima, minima, or points of inflection. The script may explain how to find and analyze critical points for functions like f(x) = x^3 - 3x^2 + 2.
Highlights

Insightful explanation of the Fundamental Theorem of Calculus.

Effective use of visual aids to explain concepts of limits and continuity.

Innovative method for solving complex integrals using substitution and integration by parts.

Clear distinction between different types of functions and their properties.

Comprehensive review of derivatives, including higher-order derivatives and their applications.

Detailed walkthrough of solving differential equations with initial conditions.

Explanation of the applications of calculus in real-world problems, such as physics and engineering.

Step-by-step approach to solving problems involving sequences and series.

Illustrative examples of Taylor and Maclaurin series.

Discussion on the importance of understanding the concept of continuity in calculus.

Practical tips for approaching multiple-choice questions efficiently.

In-depth analysis of common pitfalls and mistakes students make in calculus problems.

Use of technology and graphing calculators to solve calculus problems.

Strategies for optimizing the use of time during the AP Calculus exam.

Emphasis on the importance of practicing previous years' problems to gain familiarity with the exam format.

Transcripts

Browse More Related Video

2019 Multiple choices 10

2019 Multiple choices 24, 25

2019 Multiple choices 18,19

2019 Multiple choices 87,88

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)

2019 Multiple choices 22,23

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusMultiple ChoiceExam Review2019 EditionMathematicsEducationalCollege PrepTest PracticeProblem SolvingAcademic