Math 14 HW 6.4.15-T Using the Central Limit Theorem

Fiorentino Siciliano
11 Mar 202310:26
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the probability of male passengers fitting through an airliner's door without bending, given their height follows a normal distribution with a mean of 69 inches and a standard deviation of 2.8 inches. It calculates the probability for an individual and for the mean height of a sample of 125 men, using the normal distribution and the central limit theorem. The script concludes that the individual probability is more relevant for comfort and safety, as it ensures a larger proportion of men can pass without bending, and notes that women are generally shorter, so a design accommodating men will inherently accommodate more women.

Takeaways
  • ๐Ÿ“Š The script discusses a statistical problem involving an airliner with 250 passengers and the probability of male passengers fitting through a doorway.
  • ๐Ÿšถโ€โ™‚๏ธ It is assumed that the heights of men follow a normal distribution with a mean of 69.0 inches and a standard deviation of 2.8 inches.
  • ๐Ÿšช The first part of the problem asks for the probability that a randomly selected male passenger can fit through a 75-inch high doorway without bending.
  • ๐Ÿ“ˆ The solution involves calculating a z-score for the height of 75 inches and using a standard normal distribution to find the probability of a man being less than 75 inches tall.
  • ๐Ÿงฎ The calculated z-score for 75 inches is 2.14, and the probability of a man being shorter than 75 inches is found to be approximately 0.9838.
  • ๐Ÿ‘ฅ The second part of the problem considers the probability that the mean height of a sample of 125 men (half of the passengers) is less than 75 inches.
  • ๐Ÿ“š The central limit theorem is applied to find the standard deviation of the sample means and to calculate the z-score for this scenario.
  • ๐Ÿ”ข The z-score for the mean height of the sample of men is calculated to be 23.96, indicating an extremely high probability that the mean height will be less than 75 inches.
  • ๐Ÿค” The script then questions which probability is more relevant for passenger comfort and safety: the individual probability (Part A) or the sample mean probability (Part B).
  • ๐Ÿ›ซ It concludes that the probability from Part A is more relevant as it directly impacts the comfort of a larger proportion of individual male passengers.
  • ๐Ÿ‘š Lastly, the script raises the question of why women are not considered in this scenario, noting that since men are generally taller, a design accommodating a suitable proportion of men will also accommodate a greater proportion of women.
Q & A

  • What is the normal distribution mean height of men in the script?

    -The mean height of men is given as 69.0 inches.

  • What is the standard deviation of the heights of men mentioned in the script?

    -The standard deviation of the heights of men is 2.8 inches.

  • What is the height of the airliner's doors?

    -The height of the airliner's doors is 75 inches.

  • What is the probability that a randomly selected male passenger can fit through the doorway without bending?

    -The probability is calculated to be approximately 0.9838, meaning about 98.38% of male passengers can fit through without bending.

  • How many passengers does the airliner carry according to the script?

    -The airliner carries 250 passengers.

  • What is the z-score for a man who is 75 inches tall in the context of the script?

    -The z-score for a man who is 75 inches tall is calculated to be 2.14.

  • How many men are assumed to be on the flight if half of the passengers are men?

    -If half of the 250 passengers are men, then there would be 125 men on the flight.

  • What is the probability that the mean height of 125 men is less than 75 inches according to the central limit theorem?

    -The probability is 1.000, indicating it is virtually certain that the mean height of 125 men would be less than 75 inches.

  • Why is the probability from Part A considered more relevant when considering the comfort and safety of passengers?

    -The probability from Part A is more relevant because it shows the proportion of individual male passengers that will not need to bend, which is a more direct measure of comfort and safety for each passenger.

  • Why are women ignored in this case according to the script?

    -Women are ignored because the design that accommodates a suitable proportion of taller men will necessarily accommodate a greater proportion of women, as men are generally taller.

  • What statistical tool is used to calculate the probabilities in the script?

    -The script uses the normal distribution and the z-score to calculate the probabilities.

  • What is the standard deviation of the sample means when considering a sample of 125 men?

    -The standard deviation of the sample means is the population standard deviation (2.8 inches) divided by the square root of the sample size (125), which is part of the calculation for the z-score in Part B.

Outlines
00:00
๐Ÿ“Š Probability of Fitting Through an Airliner Door

The first paragraph discusses a statistical problem involving an airliner with 250 passengers and doors that are 75 inches high. The heights of men are normally distributed with a mean of 69.0 inches and a standard deviation of 2.8 inches. The task is to find the probability that a randomly selected male passenger can fit through the door without bending. This involves calculating the probability using a normal distribution with the given parameters. A z-score is calculated for a height of 75 inches, which is 2.14, indicating the number of standard deviations above the mean. Using a statistical tool like StatCrunch, the probability that a man's height is less than 75 inches is found to be approximately 0.9838, or 98.38%.

05:04
๐Ÿ“š Application of the Central Limit Theorem to Mean Height

The second paragraph extends the discussion to the probability that the mean height of a sample of 125 men (half of the passengers) is less than 75 inches, using the Central Limit Theorem. The mean height remains 69 inches, but the standard deviation of the sample means is calculated as 2.8 divided by the square root of 125. The z-score for the sample mean height is calculated to be 23.96, which is an extremely high value indicating a very low probability of the mean height being less than 75 inches. The probability is found to be 1.000, suggesting that it is virtually certain that the mean height of the sample will be below the door height.

10:05
๐Ÿค” Relevance of Probability in Passenger Comfort and Safety

The final paragraph considers the relevance of the calculated probabilities in the context of passenger comfort and safety. It is argued that the probability from Part A, which shows the proportion of men who do not have to bend to fit through the door, is more relevant than the probability from Part B, which concerns the mean height of samples of men. The reasoning is that ensuring a large proportion of men can fit comfortably is more important than ensuring the mean height of male passengers on flights is below the door height, as individual heights can still vary significantly. The paragraph also raises a question about the exclusion of women from the analysis, suggesting that the general difference in height between men and women might justify focusing on men's heights for door design.

Mindmap
Keywords
๐Ÿ’กAirliner
An airliner refers to a large fixed-wing aircraft designed for transporting passengers and cargo. In the context of the video, the airliner carries 250 passengers and is the subject of a discussion about door height and passenger comfort. The airliner's capacity and design are central to the problem presented in the script.
๐Ÿ’กNormal Distribution
Normal distribution, also known as Gaussian distribution, is a probability distribution that is characterized by a bell-shaped curve. It is used in the video to describe the distribution of men's heights, with a mean of 69.0 inches and a standard deviation of 2.8 inches. This statistical concept is essential for calculating the probability that a randomly selected male passenger can fit through the doorway without bending.
๐Ÿ’กMean
The mean, often referred to as the average, is a measure of central tendency in statistics. In the video, the mean height of men is given as 69.0 inches, which is a key parameter in the normal distribution used to calculate probabilities related to passenger height and the airliner's door height.
๐Ÿ’กStandard Deviation
Standard deviation is a measure that represents the amount of variation or dispersion in a set of values. In the script, the standard deviation of men's heights is 2.8 inches, which, along with the mean, helps define the normal distribution and is crucial for calculating the z-score and probabilities.
๐Ÿ’กZ-Score
A z-score is a statistical measurement that indicates how many standard deviations an element is from the mean. In the video, the z-score is calculated to determine the probability that a male passenger's height is less than the door height of 75 inches. The z-score calculation is central to solving the probability problem presented.
๐Ÿ’กProbability
Probability is a measure of the likelihood that a particular event will occur, expressed as a number between 0 and 1. The video discusses the probability of a male passenger fitting through the door without bending and the probability of the mean height of a group of men being less than the door height, using the normal distribution and z-scores.
๐Ÿ’กCentral Limit Theorem
The central limit theorem is a statistical theory that states that the distribution of sample means will be approximately normal, regardless of the shape of the population distribution, given a sufficiently large sample size. In the script, the central limit theorem is applied to find the probability that the mean height of 125 men is less than 75 inches.
๐Ÿ’กStatCrunch
StatCrunch is a statistical software tool used for data analysis and graphics. In the video, StatCrunch is mentioned as the tool used to calculate the probabilities associated with the z-scores. It is an example of how technology aids in solving complex statistical problems.
๐Ÿ’กPassenger Comfort and Safety
Passenger comfort and safety are the main concerns addressed in the video. The discussion revolves around the dimensions of the airliner's doors and the heights of male passengers, emphasizing the importance of designing spaces that accommodate the majority of users without discomfort.
๐Ÿ’กGender Differences
The script briefly touches on the general difference in height between men and women, noting that since men are typically taller, a design that accommodates a suitable proportion of men will necessarily accommodate a greater proportion of women. This point is made in the context of discussing why women are not explicitly considered in the probability calculations.
Highlights

An airliner's door height is 75 inches, and the probability of a male passenger fitting through without bending is to be calculated.

The heights of men are normally distributed with a mean of 69.0 inches and a standard deviation of 2.8 inches.

The probability calculation involves using a normal distribution with given parameters.

The z-score for a 75-inch height is calculated to be 2.14 using the formula (X - mean) / standard deviation.

The probability that a randomly selected male passenger can fit through the door is approximately 0.9838.

The central limit theorem is applied to find the probability of the mean height of a sample of 125 men being less than 75 inches.

The standard deviation of the sample means is calculated as the original standard deviation divided by the square root of the sample size.

The z-score for the mean height of 125 men is found to be 23.96, indicating a probability of 1.000.

The probability from Part A is more relevant for comfort and safety considerations, as it shows the proportion of men who do not need to bend.

Women are generally ignored in this scenario because a design accommodating a suitable proportion of taller men will also accommodate a greater proportion of women.

The design focus is on ensuring a large proportion of passengers, particularly men, can comfortably fit through the doorway.

The use of the normal distribution curve is essential for determining the probability of fitting through the door without bending.

The transcript demonstrates the application of statistical methods to real-world problems, such as airliner door design.

The calculation of z-scores is a critical step in determining probabilities in normal distributions.

The transcript provides a step-by-step guide on how to calculate probabilities using a normal distribution.

The central limit theorem is crucial for understanding the distribution of sample means in large populations.

The transcript highlights the importance of considering both individual and sample probabilities in design decisions.

The probability calculation for Part B is simplified by the central limit theorem, yielding a probability of 1.000.

Transcripts

Browse More Related Video

Math 14 HW 6.4.12-T Using the Central Limit Theorem

Using the Empirical rule to determine the approximate percentage of data less than a given value

Sampling distribution example problem | Probability and Statistics | Khan Academy

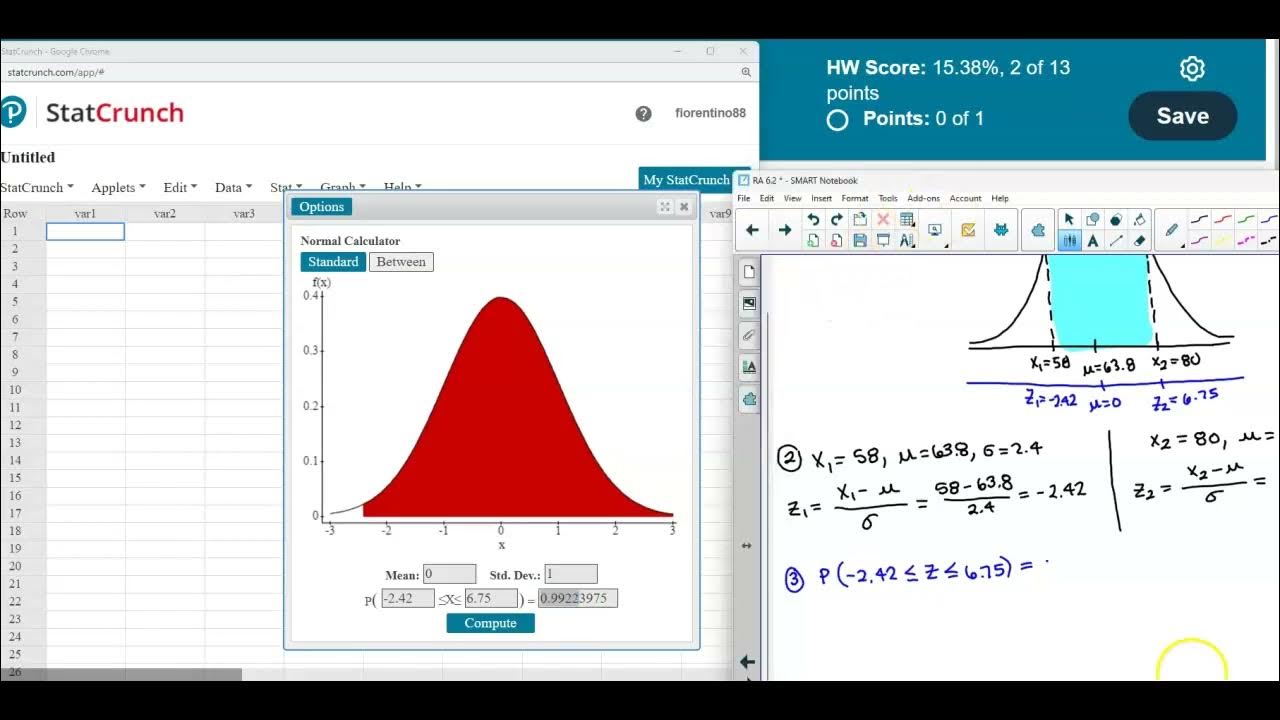
Math 14 6.2.25 Find the percentage of women meeting the height requirement.

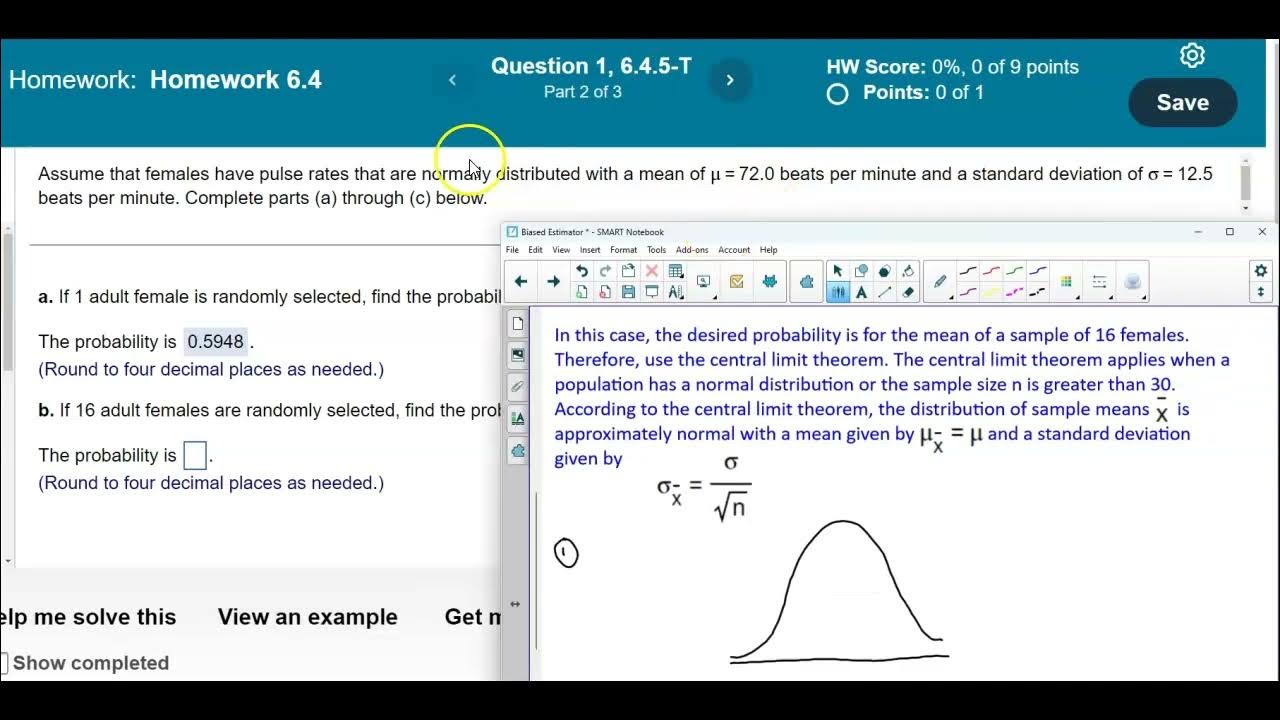
Math 14 HW 6.4.5-T Using the Central Limit Theorem

Math 14 HW 6.4.7-T Using the Central Limit Theorem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ProbabilityStatisticsAirlinerPassenger HeightNormal DistributionZ-ScoreCentral Limit TheoremSafety DesignGender HeightStatistical Analysis