Calculus AB Lesson 4.2: Related Rates

Michelle Krummel

3 Dec 201763:38

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video tutorial introduces the concept of implicit differentiation and its application in solving related rates problems. The instructor demonstrates step-by-step solutions, starting with simplifying equations before differentiation to avoid complications. Examples include finding the rate of change of a sphere's radius, the volume of a cone, and the distance and angle of elevation changes as a rocket ascends. The video employs a five-step process: drawing and labeling diagrams, identifying given and sought rates, forming equations relating variables, differentiating with respect to time, and substituting known values to solve for the desired rate.

Takeaways

🔍 Implicit differentiation is used to solve related rates problems.
✏️ Derivative of s^2 = sqrt(1 - 3t) using implicit differentiation results in ds/dt = -3/(4s sqrt(1 - 3t)).
➗ Simplifying before differentiation can sometimes make the process easier.
🧮 Using the chain rule is essential for implicit differentiation.
🔄 Derivatives of trigonometric functions often involve multiple chain rules.
⚖️ Simplifying the equation before differentiating can avoid complex rules like the quotient rule.
📐 For related rates problems, we differentiate with respect to time to find rates of change.
💡 In the example of a spherical balloon, the formula V = 4/3 π r^3 is used to relate volume and radius.
🔧 Key steps include drawing a picture, identifying given and needed rates, writing an equation, differentiating, and substituting values.
🚀 Related rates problems often involve differentiating geometric formulas to find how one variable's rate of change affects another.

Q & A

What is the main topic of the video?
-The main topic of the video is the use of implicit differentiation to solve related rates problems, with a focus on various mathematical scenarios involving rates of change.
Why might solving for 's' in the equation s squared equals the square root of 1 minus 3t be complicated?
-Solving for 's' in the given equation could be complicated because it involves taking the square root of both sides, which leads to a plus or minus situation and requires the use of the power rule combined with the chain rule when differentiating.
What is implicit differentiation and why is it used in this video?
-Implicit differentiation is a technique used to find the derivative of an equation where the variable of interest does not appear explicitly as a function of the independent variable. It is used in this video to solve related rates problems without first needing to express one variable explicitly in terms of another.
How does the video approach the problem of finding ds/dt for the equation s squared equals the square root of 1 minus 3t?
-The video approaches this by using implicit differentiation, taking the derivative of each term with respect to 't', and then solving for ds/dt by manipulating the resulting equation.
What is the significance of the 'plus or minus' in the equation s equals plus or minus the square root of the square root of 1 minus 3t?
-The 'plus or minus' indicates that there are two possible solutions for 's', one positive and one negative. However, in the context of the video, the focus is on the process of differentiating the equation rather than solving for 's'.
How does the video simplify the process of finding the derivative of 1/v when v equals secant squared of 3t plus 1?
-The video simplifies the process by taking the reciprocal of both sides of the equation to transform it into v equals secant squared of 3t plus 1, which allows for a more straightforward application of differentiation rules.
What is the purpose of the activity involving a spherical balloon being inflated at a constant rate?
-The purpose of the activity is to apply the concepts of related rates to a real-world scenario, specifically to find how fast the radius of the balloon is changing at a given instant when the balloon's diameter is a certain size.
How is the volume of a sphere related to its radius in the context of the balloon inflation problem?
-The volume of a sphere is related to its radius by the formula V = 4/3 * π * R^3. This formula is used to express the volume in terms of the radius and to find the rate of change of the volume with respect to time.
What is the relationship between the rate of change of the volume (dV/dt) and the rate of change of the radius (dr/dt) of a sphere?
-The relationship is given by the derivative of the volume formula with respect to time, which results in dV/dt = 4 * π * R^2 * dr/dt. This equation relates the rate at which the volume is changing to the rate at which the radius is changing.
How does the video solve for dr/dt when the diameter of the balloon is 12 inches?
-The video substitutes the given values into the derived equation dV/dt = 4 * π * R^2 * dr/dt, simplifies the equation, and solves for dr/dt, which turns out to be 5/(36 * π) inches per second.
What mathematical concept is demonstrated by the problem of gravel being poured into a conical pile?
-The problem demonstrates the concept of related rates, specifically how the rate of change of the volume of the pile (dV/dt) is related to the rate of change of the radius and height of the cone as gravel is added.
How does the video approach the problem of air leaking out of a sphere-shaped balloon?
-The video uses a step-by-step process to solve the problem: drawing a picture, writing down the given and needed rates, writing an equation relating volume and radius, differentiating that equation with respect to time, and substituting known values to solve for the unknown rate of change of the radius (dr/dt).
What is the formula for the volume of a sphere and how is it used in the video?
-The formula for the volume of a sphere is V = 4/3 * π * R^3. In the video, this formula is used to relate the volume and radius of the balloon, which is then differentiated with respect to time to solve for the rate of change of the radius as air leaks out.
How does the video simplify the equation for the volume of a cone in terms of its height?
-The video uses the relationship between the radius and height of the cone (R = 3H/4) to eliminate the radius variable, resulting in a simplified volume equation in terms of height only: V = (3π/16) * H^3.
What is the relationship between the rate of change of the height of the water in a tank (dH/dt) and the rate of change of the volume of the water (dV/dt)?
-The relationship is given by the derivative of the volume equation with respect to time, which results in dV/dt = (3π/16) * (dH/dt) * H^2. This equation relates the rate at which the volume is changing to the rate at which the height of the water is changing.
How does the video solve for dH/dt when the water in the tank is three feet deep?
-The video substitutes the given values into the derived equation dV/dt = (3π/16) * H^2 * dH/dt, simplifies the equation, and solves for dH/dt, which turns out to be 0.25 feet per minute.
What is the process for solving related rates problems as demonstrated in the video?
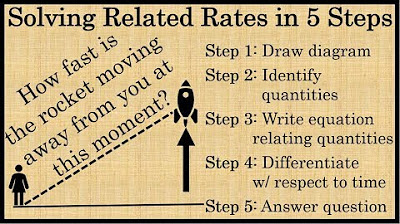
-The process involves five steps: 1) Draw and label a picture of the scenario, 2) Write down the given rate and the rate you need to find, using proper notation, 3) Write an equation that relates the variables in the rates, 4) Differentiate both sides of the equation implicitly with respect to time, and 5) Substitute all known values into the differentiated equation and solve for the unknown rate.
How does the video demonstrate the application of implicit differentiation in the context of a rocket launching?
-The video sets up a scenario where a rocket is launching vertically, and the rate of change of its height (dy/dt) and the distance from a camera to the rocket (dZ/dt) are related. It uses implicit differentiation to relate these rates and solve for the rate of change of the distance as the rocket ascends.
What trigonometric identity is used in the video to relate the angle of elevation of a camera to the rocket's height and the distance from the camera to the launch pad?
-The video uses the tangent identity, which states that the tangent of an angle (theta) is equal to the opposite side (y) divided by the adjacent side (4,000 feet in this case), or tan(theta) = y/4,000.
How does the video solve for the rate of change of the angle of elevation (dtheta/dt) when the rocket has risen 3,000 feet?
-The video uses the derived equation involving the tangent and secant functions, substitutes the known values for dy/dt, y, and Z, and solves for dtheta/dt, which turns out to be approximately 0.096 radians per second or about 5.5 degrees per second.

Outlines

00:00

📚 Introduction to Implicit Differentiation

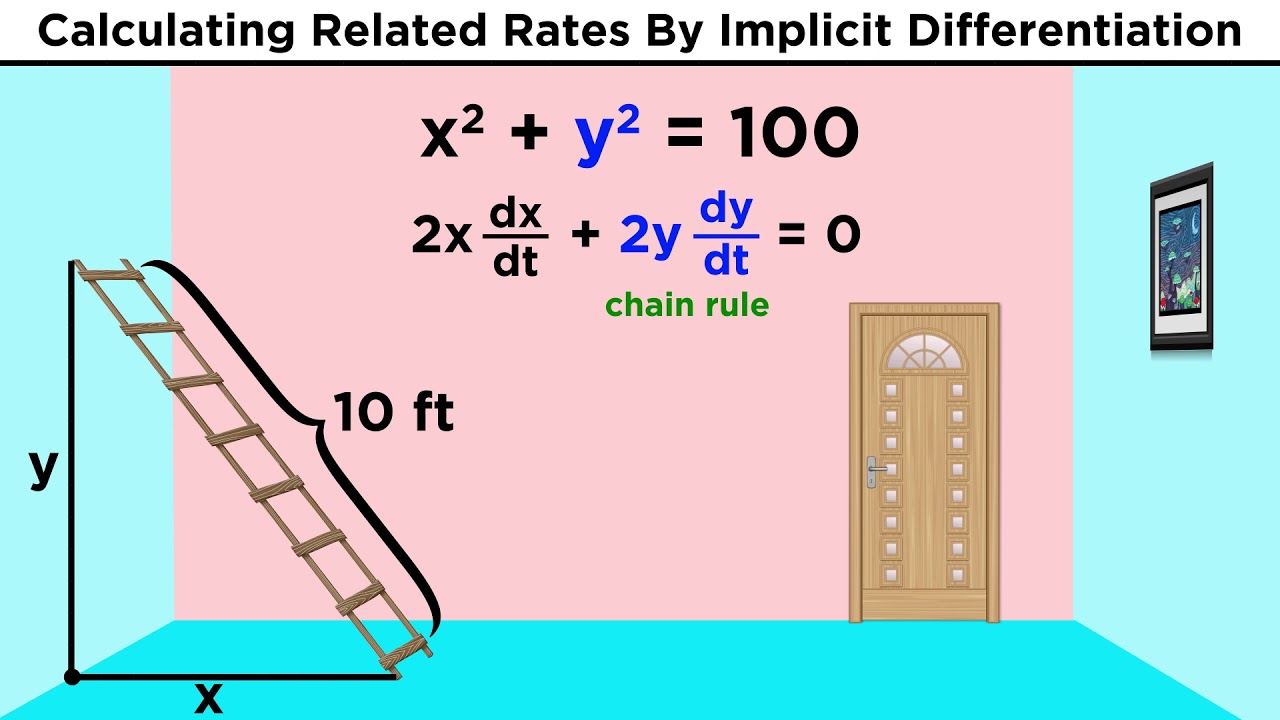
The video begins with an introduction to implicit differentiation, a method used to find derivatives when the function cannot be explicitly solved for 'y'. The instructor demonstrates how to differentiate both sides of an equation with respect to 't', using the chain rule to adjust for the variable change. The process is illustrated by taking the derivative of 's squared' with respect to 't', resulting in '2s * ds/dt', and then solving for 'ds/dt' in the context of a given equation.

05:00

🔍 Solving Related Rates Problems

The instructor moves on to related rates problems, starting with simplifying expressions before differentiating. The video covers various scenarios, such as finding 'ds/dt' and 'dv/dt' for different equations involving trigonometric functions and exponential growth. The process involves implicit differentiation and choosing the right moment to simplify expressions to make the derivative easier to compute.

10:03

🌐 Application to a Sphere's Inflation

This section applies the concepts of related rates to a real-world problem of a spherical balloon being inflated. The volume of the sphere is given by 'V = 4/3 * π * R^3', and the task is to find how the radius 'R' changes over time 't' when the volume is increasing at a constant rate. The video demonstrates how to differentiate the volume equation with respect to time and solve for 'dR/dt' using the given rate of volume change.

15:05

📉 Implicit Differentiation in Geometry

The video script delves into using implicit differentiation to solve problems in geometry, such as the surface area and volume of a sphere, cone, and cylinder. Each geometric shape has an associated equation, and the script explains how to differentiate these equations with respect to time 't' to find the rates of change for various dimensions of the shapes.

20:06

🚀 Related Rates in Motion Problems

The script introduces a problem involving a rocket's vertical ascent and a camera's need to adjust its angle of elevation and focus to track the rocket. The Pythagorean theorem is used to relate the distance 'Z' between the camera and the rocket, the horizontal distance 'X', and the vertical distance 'Y' the rocket has risen. The focus is on finding 'dZ/dt', the rate at which the distance is changing, given the rocket's speed 'dy/dt'.

25:07

📹 Camera Tracking and Angle of Elevation

Building on the previous problem, the script addresses part B, which involves the camera's angle of elevation 'θ'. The goal is to find 'dθ/dt', the rate at which the angle is changing, using the tangent function and implicit differentiation. The script provides a step-by-step approach to finding the derivative of the angle with respect to time, given the known rates and values.

30:08

🔧 Summary of the Related Rates Process

The final paragraph summarizes the five-step process for solving related rates problems. It emphasizes the importance of drawing and labeling a diagram, writing down given and sought rates, forming an equation that relates the variables, differentiating both sides of the equation with respect to time, and finally substituting known values to solve for the unknown rate.

Mindmap

Keywords

💡Implicit Differentiation

Implicit differentiation is a method used to find the derivative of an equation that is not explicitly solvable for the variable of interest. It is a key concept in the video, as the instructor demonstrates how to apply this technique to solve related rates problems without first isolating the variable. For example, the script describes using implicit differentiation to find 'ds/dt' for an equation involving 's squared' and 't', showcasing its utility in scenarios where direct differentiation would be cumbersome.

💡Related Rates

Related rates problems involve finding the rate of change of one quantity given the rate of change of another related quantity. The concept is central to the video's theme, as it ties together the various mathematical examples presented. The script illustrates this with scenarios such as the changing radius of a balloon and the rising water level in a tank, where the rate of change of one variable is calculated based on the known rate of another.

💡Chain Rule

The chain rule is a fundamental principle in calculus for differentiating composite functions. In the video, the chain rule is essential for implicit differentiation, as it allows the calculation of derivatives of complex expressions involving inner functions. The script mentions using the chain rule when differentiating 's squared' with respect to 't', highlighting its importance in navigating through the variables and their dependencies.

💡Product Rule

The product rule is a calculus rule for differentiating the product of two functions. The video script references the product rule in the context of differentiating expressions like 'R squared H', where both 'R' and 'H' are functions of 't'. The product rule is crucial for finding the derivative of each part of the expression and understanding how the rates of change interact.

💡Quotient Rule

The quotient rule is used to differentiate a quotient of two functions. Although not explicitly mentioned in the script, the concept is implicitly discussed when simplifying expressions to avoid its use, as seen in the example of multiplying both sides of an equation by 'R' to eliminate the quotient before differentiating.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are used in various examples throughout the script, particularly in the context of differentiating expressions involving these functions. The instructor demonstrates how to apply the chain rule to trigonometric functions raised to a power, as seen in the derivative of 'secant squared' with respect to 't'.

💡Pythagorean Theorem

The Pythagorean theorem is a fundamental principle in geometry relating the sides of a right triangle. In the video, the theorem is applied to relate the rates of change in a right triangle's legs and hypotenuse, as demonstrated in the example of a rocket's angle of elevation and distance from a camera.

💡Surface Area

The surface area of a geometric shape, such as a sphere or a cone, is a measure of the total area occupied by the surface of the shape. The script discusses the surface area of a sphere and how its rate of change (dA/dt) is related to the rate of change of the radius (dr/dt), illustrating the application of related rates in geometry.

💡Volume

Volume is the measure of the space occupied by a three-dimensional object. The video script frequently refers to the volume of geometric shapes like spheres and cones, and how the rate of change of volume (dV/dt) is connected to the rates of change of other dimensions, such as radius or height, through related rates problems.

💡Simplification

Simplification in calculus involves rewriting expressions to make differentiation easier. The script emphasizes the importance of simplifying before differentiating, such as converting '1/V' to 'V' and 'cosine squared' to 'secant squared', to avoid complex derivatives and make the problem more manageable.

💡Constant Multiple Rule

The constant multiple rule states that the derivative of a constant times a function is the constant times the derivative of the function. This rule is implicitly used in the script when differentiating terms like '4/3 * pi * R cubed', where the constant '4/3 * pi' is factored out before differentiating the 'R cubed' term.

Highlights

Introduction to using implicit differentiation to solve related rates problems.

Deciding against solving for 's' explicitly in the equation s^2 = √(1 - 3t) due to complexity.

Explaining the process of implicit differentiation and applying the chain rule.

Differentiating both sides of an equation to relate rates of change.

Simplifying the derivative process by rewriting expressions before differentiating.

Comparing methods of differentiating trigonometric functions with and without simplification.

Finding the rate of change of the radius of a spherical balloon being inflated.

Relating the rates of change of volume and radius for a balloon using the volume formula.

Solving for the rate of change of the radius at a specific diameter.

Comparing the rate of change of the radius at different diameters of the balloon.

Differentiating the surface area formula of a sphere to relate area and radius rates.

Applying implicit differentiation to the volume formula of a cone.

Using the product rule to differentiate the volume formula of a cylinder.

Differentiating the Pythagorean theorem to relate the rates of change of triangle sides.

Relating the rate of change of an angle to the rate of change of a side in a right triangle.

Describing a related rates problem involving a conical pile of gravel and its increasing volume.

Solving a related rates problem for the rate of change of a balloon's radius as air leaks out.

Using similar triangles to relate the radius and height of a cone filled with water.

Differentiating the volume equation of a cone to find the rate of change of water level.

Calculating the rate of change of the angle of elevation of a camera tracking a rocket.

Using trigonometric differentiation to find how fast a camera's angle of elevation is changing.

Transcripts

Browse More Related Video

Related Rates

Related Rates in Calculus

3.8/3.9 - Implicit Differentiation and Related Rates

How to Solve Related Rates Problems in 5 Steps :: Calculus

Calculus 1 Lecture 2.8: Related Rates

Math1325 Lecture 11-4 - Related Rates

Related Tags

Implicit Differentiation Related Rates Mathematics Tutorial Trigonometry Problems Calculus Concepts Educational Content Geometry Examples Rate of Change Sphere Volume Cone Volume