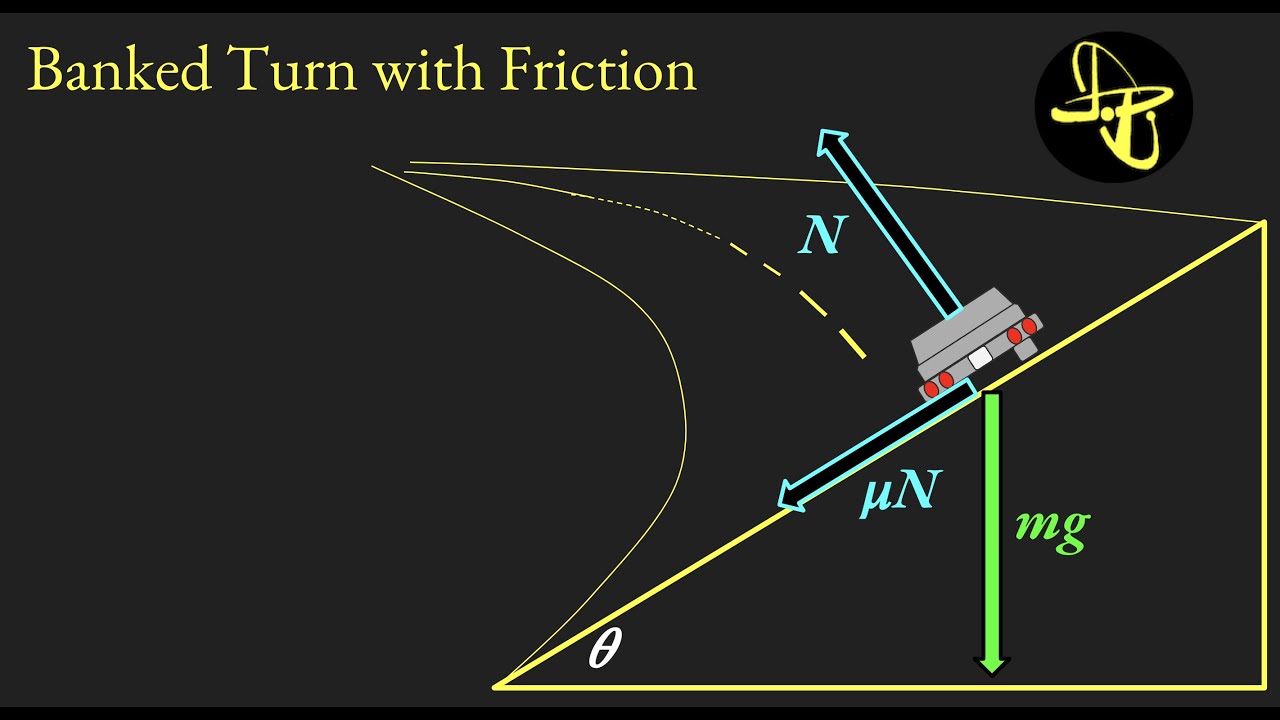
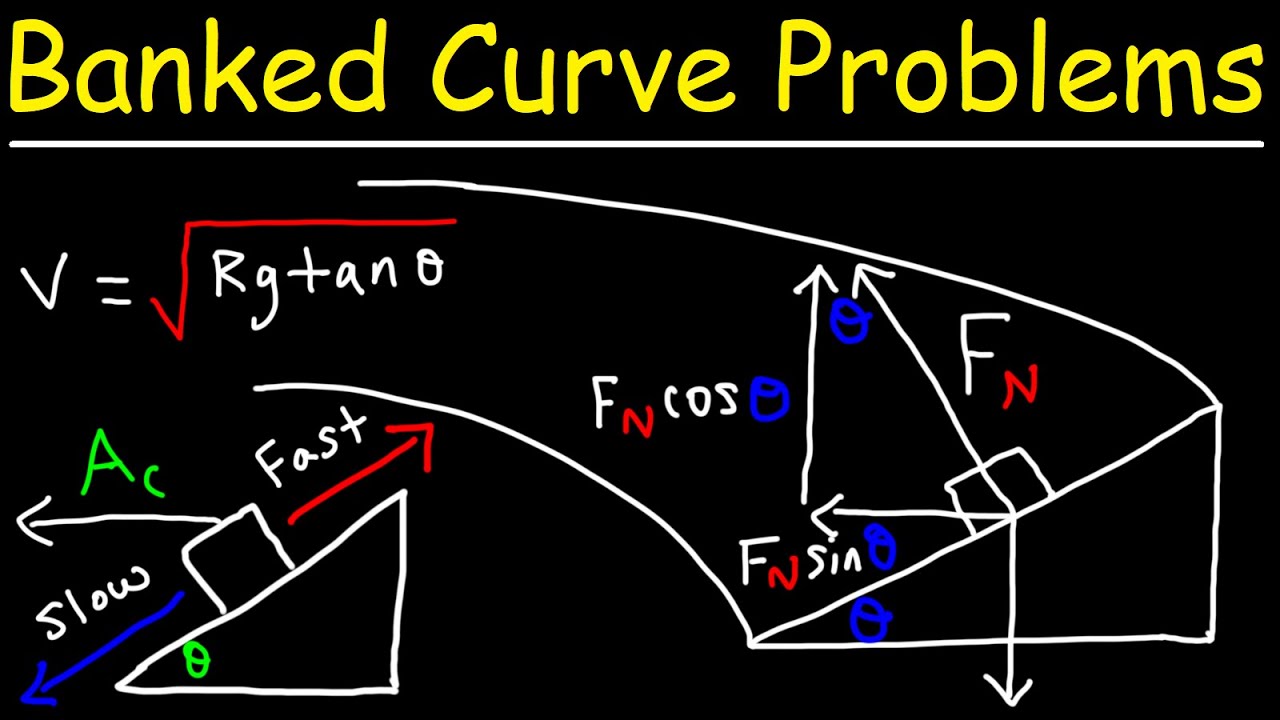
Maximum Speed Around a Banked Curve WITH Friction
TLDRIn this educational video, the host explores the physics behind a car navigating a banked curve with friction. They introduce a hypothetical scenario with a 2,000 kg car, a 0.3 coefficient of static friction, a 15-degree bank angle, and a 40-meter radius curve. By applying the momentum principle and friction model, the host calculates the maximum and minimum speeds at which the car can travel without losing grip. The video provides a detailed explanation of the forces involved, including gravitational, normal, and frictional forces, and how they contribute to the car's circular motion. The host also checks the calculations for a flat curve scenario and a steep bank angle, ensuring the physics holds true in various situations.
Takeaways
- 🚗 The video discusses the physics of a car turning on different types of curves: flat, banked with no friction, and a vertical wall (Wall of Death).
- 🔢 The presenter uses specific numerical values for mass (2000 kg), coefficient of static friction (0.3), bank angle (15 degrees), and radius of the curve (40 meters) to illustrate the calculations.
- 📚 The momentum principle is introduced, stating that the net force on an object is related to the change in momentum, with the rate of change in momentum being mass times velocity squared over the radius of the circle.
- 🔄 The direction of the change in momentum is toward the center of the circle, which is key in understanding circular motion.
- 📐 Friction is modeled as the force that depends on the normal force, with the maximum frictional force being the coefficient of static friction times the normal force.
- 📈 A force diagram is created to visualize the forces acting on the car: gravitational force, normal force, and frictional force.
- 🧭 The acceleration of the car is in the X direction towards the center of the circle, which is crucial for setting up the equations.
- ⚖️ The normal force is calculated using trigonometric relationships and the given coefficient of static friction.
- 🔢 The maximum speed the car can go without losing traction on the banked curve is found by setting up and solving equations for the forces in the X and Y directions.
- 🔄 The minimum speed the car needs to maintain to avoid sliding down the banked track is also discussed, highlighting the importance of frictional force.
- 📚 The presenter checks the calculations for special cases, such as when the bank angle is zero (flat curve) and when the angle is very large, to ensure the formulas make sense and are accurate.
Q & A
What is the main topic of the video?
-The main topic of the video is the physics of a car turning around a banked curve with friction, specifically how fast it can go while staying on the road.
What are the three types of curves discussed in the video?
-The three types of curves discussed are a flat curve, a banked curve with no friction, and a vertical wall known as the Wall of Death.
What are the hypothetical values given for the car's mass and coefficient of static friction?
-The hypothetical values given for the car's mass are 2,000 kilograms and the coefficient of static friction is 0.3.
What is the bank angle (Theta) and radius of the curve used in the calculations?
-The bank angle (Theta) used in the calculations is 15 degrees and the radius of the curve is 40 meters.
What principle from physics is used to analyze the car's motion on the curve?
-The momentum principle is used to analyze the car's motion on the curve, which relates the net force on an object to the change in its momentum.
How is the frictional force related to the normal force?
-The frictional force is related to the normal force by the equation that the frictional force is less than or equal to the coefficient of static friction times the normal force.
What is the direction of the car's acceleration when moving in a circular path?
-The direction of the car's acceleration when moving in a circular path is towards the center of the circle, which is the direction of the change in momentum.
What are the two forces considered in the X-direction for the car on the banked curve?
-The two forces considered in the X-direction for the car on the banked curve are the component of the normal force (FN times sine Theta) and the horizontal component of the frictional force (frictional force times cosine Theta).
How is the maximum speed of the car calculated?
-The maximum speed of the car is calculated by setting up an equation that considers the forces acting on the car and solving for the velocity (V) that satisfies the condition for no change in momentum in the Y-direction and circular motion in the X-direction.
What is the significance of checking the units in the equations used in the video?
-Checking the units in the equations ensures that the calculations are physically meaningful and that the units on both sides of the equation are consistent, which is crucial for the validity of the physics involved.
How does the video script handle the special case when Theta equals zero?
-When Theta equals zero, which represents a flat curve, the script shows that the normal force equals the weight of the car, and the maximum speed formula simplifies to the case previously discussed for a flat curve without banking.
What happens if the bank angle (Theta) is very large?
-If the bank angle (Theta) is very large, there is a minimum speed the car must maintain to prevent sliding down the track. The direction of the frictional force changes, and the calculations for minimum speed would need to account for this change.
What is the final maximum speed calculated for the car in the video?
-The final maximum speed calculated for the car in the video is approximately 34.9 miles per hour.
Outlines
🔍 Introduction to Banked Curves with Friction
The video begins with an introduction to the physics problem of a car navigating a banked curve with friction. The host outlines previous videos on flat and banked curves without friction and a 'Wall of Death' scenario. The current focus is on calculating the speed at which a car can safely navigate a banked curve with friction. Key parameters are introduced: a car with a mass of 2,000 kg, a static friction coefficient of 0.3, a bank angle of 15 degrees, and a curve radius of 40 meters. The momentum principle is discussed, relating the net force on an object to its change in momentum, with the aim of combining knowledge of forces and momentum change to solve the problem.
📚 Applying Physics Principles to Banked Curves
This paragraph delves into the physics behind a car on a banked curve with friction. The host explains the need to calculate the net force and momentum in both the x and y directions separately. A force diagram is introduced, illustrating the gravitational force, normal force, and frictional force acting on the car. The host uses trigonometric relationships to break down these forces into components and sets up equations for the net force in the y and x directions. The goal is to find the speed at which the car can maintain its circular path without slipping, leading to a discussion on the maximum frictional force in relation to the normal force.
🧩 Solving for Speed on a Banked Curve
The host continues the physics problem by setting up equations to solve for the unknowns: speed, friction, and normal force. Using the third equation that relates the friction force to the coefficient of static friction and the normal force, the host simplifies the equations to solve for the normal force as a function of the car's weight, angle of the bank, and friction coefficient. This leads to an expression for the car's velocity squared in terms of the normal force, which is then substituted back into the equation to find the maximum speed the car can travel without losing traction on the curve.
🔢 Calculating Maximum and Minimum Speeds
In this section, the host performs the actual calculations for the maximum speed the car can travel on the banked curve with friction. The host plugs in the given values for the angle, radius, gravitational acceleration, and friction coefficient to find the maximum speed in meters per second, which is then converted to miles per hour. Additionally, the host considers the scenario of a very large bank angle, discussing the minimum speed required to prevent the car from sliding down the track. The host emphasizes the importance of checking units and special cases, such as when the bank angle is zero, to ensure the calculations are correct and meaningful.
Mindmap
Keywords
💡Bank curve
💡Friction
💡Momentum principle
💡Normal force
💡Coefficient of static friction
💡Mass
💡Radius of the curve
💡Centripetal force
💡Circular motion
💡Acceleration
💡Force diagram
Highlights
The video discusses the physics of a car turning around a banked curve with friction.
A 2,000 kg car with a 0.3 static friction coefficient is used for the calculations.
The bank angle (Theta) is set at 15 degrees with a curve radius of 40 meters.
The momentum principle is applied to understand the change in momentum during circular motion.
Frictional force is modeled as the product of the coefficient of static friction and the normal force.
A force diagram is created to visualize the forces acting on the car during the turn.
The direction of acceleration for the object is in the X direction, towards the center of the circle.
The net force in the Y direction is calculated to ensure no vertical movement.
The net force in the X direction is related to the circular motion and is set to mv^2/R.
Three unknowns (V, friction, normal force) are present, necessitating a third equation for solution.
The maximum friction force is used to solve for the normal force.
Units are checked to ensure the correctness of the equations and calculations.
A special case for Theta equals zero (flat curve) is analyzed.
The formula for maximum speed is derived and simplified.
Values are substituted into the formula to calculate the maximum speed the car can go.
A conversion from meters per second to miles per hour is performed to interpret the result.
The minimum speed required to prevent sliding down the track for a very large Theta is discussed.
The direction of frictional force changes for different scenarios, affecting the calculations.
A link to a related video on banked curves without friction is provided for further understanding.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: