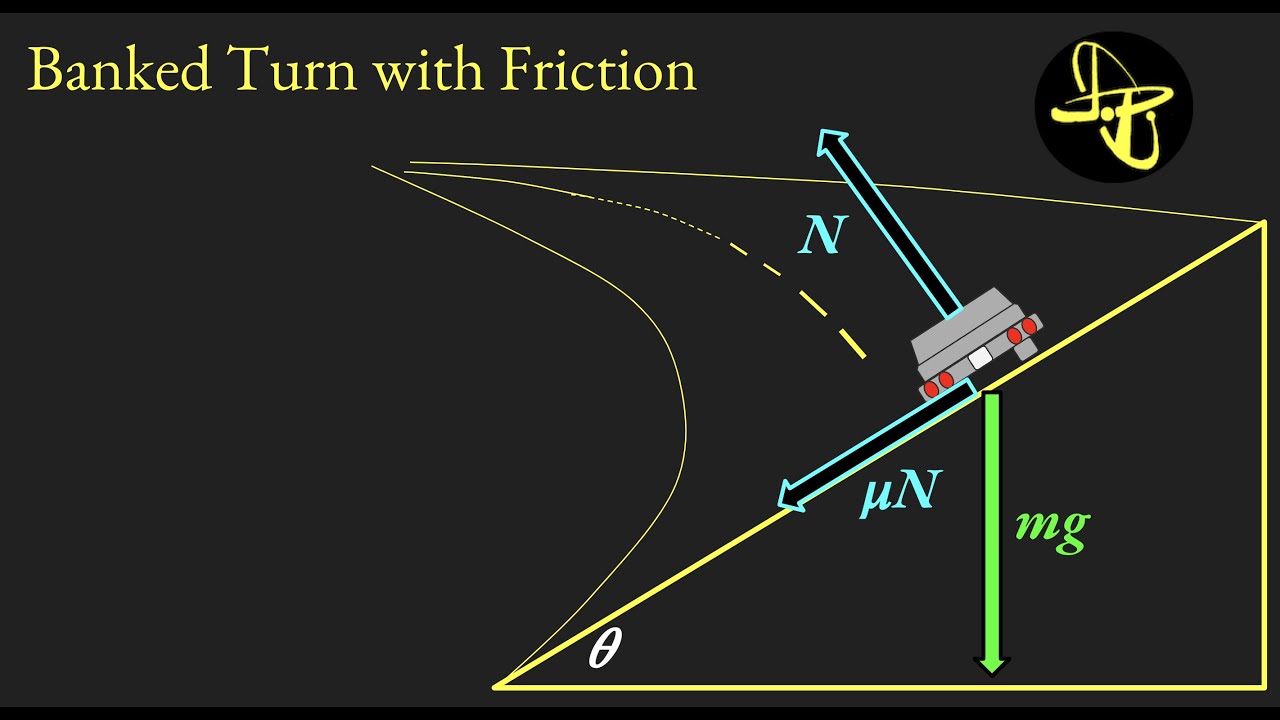
Banked Curve with Friction: Finding Maximum and Minimum Speed
TLDRIn this educational video, Physics Ninja explores the impact of friction on the speed at which a car can safely navigate a banked curve. Initially, the channel examined this scenario without friction, but now includes it to find the maximum and minimum safe speeds. By analyzing a free-body diagram and applying the principles of static friction and centripetal force, the video derives equations for both the minimum and maximum velocities. Using the example of Talladega racetrack, the calculations are put to the test, revealing that with friction, cars can safely go faster than previously thought, closely aligning with real-world racing records.
Takeaways
- 🔧 The video discusses the physics of driving a car around a banked curve with friction considered.
- 📐 It uses a cross-sectional view of the car on the slope and labels forces acting on it, including friction.
- 🔄 The 'slow case' scenario is analyzed where not enough speed causes the car to deviate from the intended circular path.
- 🚫 Friction is shown to oppose the car's motion, with static friction playing a crucial role in maintaining the path.
- ⚖️ Forces are broken down into vertical and horizontal components to understand their impact on the car's trajectory.
- 🔄 The 'fast case' scenario is also examined where excessive speed results in a larger radius than intended.
- 📉 The video derives equations for both the slow and fast cases to find the minimum and maximum safe speeds.
- 📚 Trigonometry is used to relate the forces and angles involved with the car's motion on the banked curve.
- 🔢 The expressions for minimum and maximum speeds are provided, highlighting the importance of the static friction coefficient.
- 🏎️ The script applies the theory to Talladega racetrack, calculating the maximum safe speed with a given static friction coefficient.
- 📈 A comparison is made with the actual record speed set by Rusty Wallace at Talladega, showing the practical application of the physics involved.
Q & A
What is the main focus of this video?
-The video focuses on calculating the maximum and minimum speeds a car can safely navigate a banked curve when friction is considered.
What forces are considered in the free body diagram for the car on the slope?
-The forces considered are the normal force, the force of static friction, and the weight of the car.
Why is static friction important in this problem?
-Static friction is important because it affects the car's ability to stay on the circular path and influences the maximum and minimum speeds the car can travel without slipping.
How is the angle theta used in the analysis?
-The angle theta is used to break down the normal force and the force of friction into their horizontal and vertical components.
What happens if the car goes too slow on the banked curve?
-If the car goes too slow, it will not stay on the circular path and will curve to a smaller radius, where friction opposes this motion to keep the car on track.
What is the significance of the centripetal acceleration equation in this context?
-The centripetal acceleration equation helps determine the acceleration toward the center of the circle, which is essential for calculating the forces needed to keep the car on the curved path.
How do the forces in the vertical direction balance out?
-In the vertical direction, the normal force's vertical component and the vertical component of static friction must balance the car's weight.
What changes when the car goes too fast around the banked curve?
-When the car goes too fast, the force of static friction acts down the ramp, adding to the normal force's component toward the center of the circle, allowing for higher speeds.
How is the expression for the minimum speed derived?
-The minimum speed expression is derived by setting up equations for the sum of forces in the x and y directions, solving for the normal force, and substituting into the centripetal force equation.
What real-world example is used to validate the calculations?
-The calculations are validated using the Talladega racetrack example, where the maximum speed with friction is compared to the actual record speed set by Rusty Wallace.
Outlines
🛞 Introduction to Friction in Banked Curves
Physics Ninja discusses adding the force of friction between the tires and the road to the previously covered banked curve example. The aim is to find the maximum and minimum speeds for safely navigating the curve. A Freebody diagram is introduced to help visualize the forces at play, focusing initially on the slow case where insufficient speed results in a smaller radius of curvature. The role of static friction and its components in both vertical and horizontal directions are analyzed, along with their contributions to maintaining the circular path.
🔧 Components of Static Friction and Normal Force
The focus shifts to breaking down the forces into vertical and horizontal components. The equations governing the normal force and the force of static friction in the X and Y directions are derived. These components are crucial for calculating the minimum speed necessary to stay on the banked curve. The video explains how these forces counteract each other and contribute to the centripetal acceleration required for circular motion. Detailed mathematical expressions for the normal force and friction components are provided, emphasizing the relationships between them.
🚗 Analyzing Forces for High-Speed Scenarios
In this section, the script examines the scenario where the car is moving too fast around the banked curve. The larger radius of curvature and the increased force requirements are discussed. The static friction now acts down the ramp, adding to the centripetal force needed to maintain the path. The equations for the normal and frictional forces are revisited, with adjustments for the high-speed case. The video demonstrates how to solve these equations to find the maximum speed, highlighting the similarities and differences in the force components compared to the slow-speed case.
🏁 Calculating Maximum Speed with Friction at Talladega
The final part of the video applies the derived equations to a real-world example at Talladega racetrack. Given specific values for the radius and angle of the track, along with a coefficient of static friction, the video calculates the maximum speed for safe navigation. This speed is compared to recorded speeds at the track, illustrating the practical application of the theoretical calculations. Adjustments for factors like track conditions and tire properties are mentioned, showing how they can affect the maximum achievable speed.
Mindmap
Keywords
💡Bank curve
💡Friction
💡Freebody diagram
💡Static friction
💡Normal force
💡Centripetal acceleration
💡Coefficient of static friction
💡Tangential speed
💡Talladega racetrack
💡Rusty Wallace
Highlights
Introduction of the physics problem involving a bank curve with friction.
Explanation of the forces acting on a car going around a bank curve without friction.
Introduction of friction between tires and road and its impact on the bank curve problem.
Description of the slow case scenario where the car might not maintain the circular path.
Analysis of the force of static friction and its maximum value.
Breakdown of forces into vertical and horizontal components for the slow case.
Use of trigonometry to determine the components of normal force and friction.
Derivation of the centripetal acceleration equation for the slow case.
Calculation of the minimum speed for safely navigating the bank curve with friction.
Setting up equations for the fast case scenario where the car might exceed the bank curve.
Explanation of how to find the maximum speed for safely navigating the bank curve.
Derivation of expressions for both minimum and maximum safe speeds.
Application of the derived formulas to the Talladega racetrack example.
Calculation of the maximum speed for Talladega racetrack considering static friction.
Comparison of calculated maximum speed with the record speed set by Rusty Wallace.
Discussion on the impact of different factors such as road conditions and tire types on the speed calculations.
Conclusion summarizing the findings and the practical implications for safe driving speeds on banked curves.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: