All of AQA Waves Explained - A Level Physics REVISION
TLDRThis educational video script delves into the physics of waves, focusing on the AQA curriculum. It explains the fundamental concepts of waves as oscillations that transfer or store energy, distinguishing between longitudinal and transverse waves. The script explores wave properties such as amplitude, wavelength, frequency, and phase difference. It also covers the phenomena of interference and diffraction, demonstrating how waves interact with each other and obstacles. Practical examples like sound waves, electromagnetic spectrum, and light polarization are given. The video further investigates stationary waves, including the formation of nodes and antinodes, and concludes with a discussion on refraction, total internal reflection, and optical fibers, highlighting their applications in telecommunications.
Takeaways
- 🌊 Waves are oscillations that can transfer or store energy, and they can be classified as progressive or stationary.
- 📏 Progressive waves transfer energy and are either longitudinal, where particle oscillations are in the direction of energy transfer, or transverse, where they oscillate perpendicular to the energy transfer.
- 📚 The key terms for waves include amplitude, wavelength (λ), time period (T), and frequency (F), with the relationship between time period and frequency being T = 1/F and F = 1/T.
- 🔄 Phase refers to the position within a wave cycle and phase difference can be used to compare different parts of a wave or different waves.
- 👂 Examples of longitudinal waves include sound waves, while transverse waves encompass the electromagnetic spectrum, which travels at the speed of light in a vacuum.
- 🔗 The speed of a wave (C) can be calculated using the equation C = Fλ, where F is the frequency and λ is the wavelength.
- 🔆 Transverse waves can be polarized, unlike longitudinal waves, which is useful in applications such as sunglasses and radio transmissions.
- 🎶 Stationary waves, formed by the interference of a wave with itself, result in nodes (no displacement) and antinodes (maximum displacement).
- 📐 The first harmonic of a stationary wave on a string can be calculated using the formula f = (1/2L) * √(T/μ), where L is the length of the string, T is the tension, and μ is the mass per unit length.
- 🌈 Interference and diffraction are properties of waves that result in patterns of constructive and destructive interference, which can be observed with light through double slits or a diffraction grating.
- 💧 Refraction occurs when a wave changes speed and direction as it passes from one medium to another, and it can be described using Snell's law and the refractive index.
Q & A
What are waves and what can they do?
-Waves are oscillations of particles or a field. They can either transfer energy or store energy.
What is a progressive wave and how does it transfer energy?
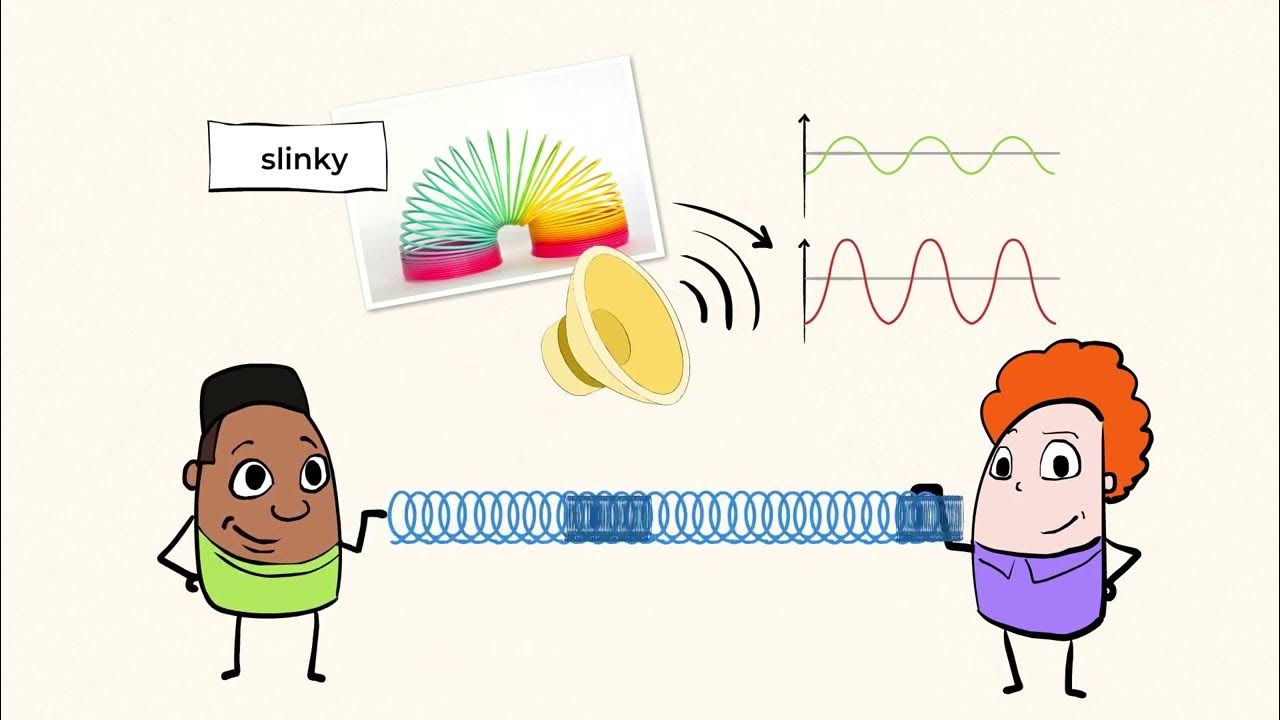
-A progressive wave is a type of wave that transfers energy from one place to another, similar to a demonstration with a slinky at school.
What are the two classifications of progressive waves?
-The two classifications of progressive waves are longitudinal waves, where particles oscillate in the same direction as the energy transfer, and transverse waves, where particles oscillate at 90 degrees to the direction of energy transfer.
What is the difference between longitudinal and transverse waves in terms of particle movement?
-In longitudinal waves, particles move in the same direction as the energy transfer, while in transverse waves, particles move perpendicular to the direction of energy transfer.
What is amplitude in the context of waves?
-Amplitude is the height of a wave, which can be represented on a graph as the displacement of a particle from its equilibrium position.
What is wavelength and how is it measured?
-Wavelength is the distance from one wave to the equivalent point on the next wave, and it can be measured peak to peak, trough to trough, or any point on one wave to the corresponding point on the next.
What is the relationship between time period (T) and frequency (F) of a wave?
-The time period (T) of a wave is the inverse of its frequency (F), which can be represented by the equation T = 1/F or F = 1/T.
What is the speed of a wave in a vacuum and how does it relate to frequency and wavelength?
-In a vacuum, waves travel at the speed of light, which is 3.00 x 10^8 meters per second. The speed of a wave (C) can be calculated using the equation C = F * lambda, where F is the frequency and lambda is the wavelength.
What is polarization and why can only transverse waves be polarized?
-Polarization is the restriction of the direction of oscillation of a transverse wave to a single plane. Only transverse waves can be polarized because their oscillations occur perpendicular to the direction of wave travel, allowing them to pass through filters that restrict motion in certain directions.
What is a stationary wave and how is it formed?
-A stationary wave is formed when a progressive wave is reflected off a surface and interferes with the original wave. This results in nodes (positions of no displacement) and antinodes (positions of maximum displacement) along the medium.
What is the first harmonic in the context of stationary waves?
-The first harmonic is a specific pattern of a stationary wave where the distance between two fixed ends of the medium is equal to half the wavelength of the wave.
What is interference in waves and how does it relate to diffraction?
-Interference occurs when two waves superimpose to form a wave of greater, lower, or the same amplitude depending on their phase relationship. Diffraction is the spreading out of waves as they pass through a gap or around an obstacle, which can lead to interference patterns.
How does the width of the fringes in a double-slit experiment relate to the wavelength, slit separation, and screen distance?
-The width of the fringes (w) in a double-slit experiment is given by the equation w = (lambda * D) / s, where lambda is the wavelength of light, D is the distance from the double slit to the screen, and s is the distance between the two slits.
What is Snell's Law and how does it relate to the refraction of light?
-Snell's Law states that N1 * sin(theta1) = N2 * sin(theta2), where N1 and N2 are the refractive indices of two different media, and theta1 and theta2 are the angles of incidence and refraction, respectively. It describes how light bends when it passes from one medium to another, changing speed.
What is total internal reflection and how is it used in optical fibers?
-Total internal reflection occurs when light travels from a more optically dense medium to a less dense medium at an angle greater than the critical angle, causing the light to be completely reflected within the denser medium. This principle is used in optical fibers to transmit light signals over long distances with minimal loss.
What are the two types of pulse broadening in optical fibers and what causes them?
-The two types of pulse broadening in optical fibers are modal dispersion and material dispersion. Modal dispersion is caused by different paths that light can take through the fiber, causing parts of the signal to arrive at different times. Material dispersion is due to different wavelengths of light traveling at different speeds within the fiber, leading to a spreading out of the signal over distance.
Outlines
🌊 Understanding Waves and Their Characteristics
The video begins with an introduction to waves, defining them as oscillations that can transfer or store energy. It distinguishes between two main types of waves: longitudinal, where particle oscillation aligns with energy transfer, and transverse, where oscillation is perpendicular to the energy transfer. Key wave parameters such as amplitude, wavelength (λ), time period (T), and frequency (F) are explained, with the relationship between time period and frequency highlighted by the equations T = 1/F and F = 1/T. The concept of wave phase is introduced, illustrating how different parts of a wave can be in or out of phase with each other. Examples of longitudinal waves include sound waves, while transverse waves encompass the electromagnetic spectrum, which travels at the speed of light (c = 3.00 x 10^8 m/s). The video also presents the wave speed equation C = Fλ, which is crucial for understanding wave behavior.
🔄 Properties of Transverse Waves and Polarization
This paragraph delves into the unique properties of transverse waves, specifically their ability to be polarized. It explains the concept of polarization using the example of a wave oscillating in a single plane and how it can be filtered by vertical or horizontal slats. The polarization of light is demonstrated through its interaction with Polaroid filters, and the relevance of polarization in everyday applications like sunglasses and radio wave transmission is discussed. The text also covers the creation of stationary waves through interference, where a progressive wave reflects off a surface and combines with itself. The properties of stationary waves, such as nodes and antinodes, are introduced, and the conditions for constructive and destructive interference are explained. Formulas related to the first harmonic of a string are provided, showing how frequency is influenced by the string's length, tension, and mass per unit length.
📏 Exploring Stationary Waves and Their Formation
The script continues the discussion on stationary waves, describing how they form through interference when a wave reflects off a surface. It explains how stationary waves can be observed in experiments with strings and vibration generators, leading to the formation of nodes and antinodes. The concept of harmonics is introduced, starting with the first harmonic and progressing to the second harmonic, with the节点 (nodes) remaining fixed at each end. The paragraph also explores the interference of waves from multiple sources, such as speakers or microwave transmitters, and how they create patterns of constructive and destructive interference. The diffraction of light through a double slit is described, resulting in a diffraction pattern that can be analyzed to understand wave behavior.
🌈 Diffraction, Interference, and the Double Slit Experiment
This section focuses on the phenomena of diffraction and interference, particularly through the double slit experiment with laser light. It describes how laser light, being monochromatic and coherent, creates a pattern of light and dark fringes on a screen after passing through two closely spaced slits. The formula relating the fringe width (w), the distance between the slits (s), the distance from the slits to the screen (D), and the wavelength of light (λ) is given as w = λD/s. The paragraph also discusses single-slit diffraction and the resulting pattern, which differs from the double-slit pattern. The effects of shining white light through a single slit are explored, resulting in a spectrum of colors due to the different wavelengths of light. The concept of a diffraction grating, which contains many closely spaced slits, is introduced, and how it can be used to measure wavelengths of light is explained.
🔍 Refraction, Total Internal Reflection, and Optical Fibers
The script shifts to the topic of refraction, which occurs when a wave changes speed and direction as it moves between different media. It explains how the refractive index (n) affects the bending of light and introduces Snell's law, which relates the angles of incidence and refraction to the refractive indices of the media. The phenomenon of total internal reflection is discussed, where light is completely reflected within a medium if the angle of incidence exceeds the critical angle. This principle is applied to the functioning of optical fibers, which are used to transmit data over long distances. The structure of optical fibers, including the core and cladding with different refractive indices, is described. The challenges of signal attenuation and pulse broadening in optical fibers are also discussed, along with methods to mitigate these issues.
📶 Digital Communications and Optical Fibers
The final paragraph summarizes the advantages of digital communications, particularly in the context of optical fibers. It explains how digital signals, consisting of pulses of light, can be transmitted over long distances with the help of booster stations to overcome signal attenuation. The paragraph addresses the issue of pulse broadening, which causes signals to become distorted over long distances. It distinguishes between two types of dispersion contributing to pulse broadening: modal dispersion, due to different light paths within the fiber, and material dispersion, due to varying travel speeds of different light wavelengths. The ability to reconstruct the original signal at the end of the transmission using electronics is highlighted, emphasizing the high-quality signal transmission achievable with digital communication systems.
📚 Conclusion and Study Resources for Waves Topic
The video concludes with a summary of the AQA A-level and AS-level waves topic, encouraging students to utilize the provided resources for exam preparation. It promotes other videos available on the channel that cover a range of physics topics in greater depth, offering over 250 videos for comprehensive study. The presenter wishes students well in their exam preparation and thanks them for watching, providing a final call to action to subscribe for more detailed revision and topic coverage.
Mindmap
Keywords
💡Waves
💡Progressive Wave
💡Longitudinal Wave
💡Transverse Wave
💡Amplitude
💡Wavelength
💡Frequency
💡Phase
💡Polarization
💡Stationary Wave
💡Interference
💡Diffraction
💡Refraction
💡Optical Fiber
Highlights
Waves are oscillations of particles or fields that can transfer or store energy.
Progressive waves transfer energy and can be demonstrated using a slinky.
Longitudinal waves have particle oscillations in the same direction as energy transfer.
Transverse waves have particle oscillations perpendicular to the direction of energy transfer.
Key wave terms such as amplitude, wavelength, time period, and frequency are defined through graphs.
The relationship between time period and frequency is explained using the equations T = 1/F and F = 1/T.
Phase of a wave is described as a factor indicating the part of the cycle the wave is in.
Examples of longitudinal waves include sound waves and ultrasound.
Transverse waves encompass the entire electromagnetic spectrum.
The speed of a wave is calculated using the equation C = F * λ.
Transverse waves can be polarized, unlike longitudinal waves.
Stationary waves, formed by interference of a wave with itself, are explained with the example of waves on a string.
Nodes and antinodes are key components of stationary waves, with nodes being points of no displacement.
The first harmonic and its calculation in terms of string properties is detailed.
Interference patterns are demonstrated with examples including sound waves, microwaves, and light.
Diffraction is explored through single and double slits, and the effects on light are visualized.
Refraction is explained as the change in direction when a wave passes from one medium to another.
Snell's law and the critical angle are discussed in the context of refraction.
Total internal reflection and its application in optical fibers are explained.
The challenges of signal loss and pulse broadening in optical fibers are discussed.
Digital communication's ability to restore signals despite challenges is highlighted.
Transcripts
Browse More Related Video

IGCSE Physics [Syllabus 3.1] Wave properties

Transverse and Longitudinal Waves

GCSE Physics - Intro to Waves - Longitudinal and Transverse Waves #61

Wave Speed on a String - Tension Force, Intensity, Power, Amplitude, Frequency - Inverse Square Law

Traveling Waves: Crash Course Physics #17
Wave behavior | MightyOwl Science | 4th Grade
5.0 / 5 (0 votes)
Thanks for rating: