Simple Harmonic Motion: Crash Course Physics #16

CrashCourse
21 Jul 201609:10
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores oscillations and simple harmonic motion, using the example of London's Millennium Bridge. It explains how the bridge's unexpected swaying was caused by resonance that amplified small oscillations. The physics of simple harmonic motion is illustrated through a ball on a spring. Using uniform circular motion, equations are derived for properties like period, frequency, and angular velocity. Finally, it's shown that the position graph of an object in simple harmonic motion is a wave, relating back to the bridge's wave-like motion.

Takeaways
  • 😀 The swaying of the Millennium Bridge was caused by oscillations, specifically simple harmonic motion
  • 👉 Simple harmonic motion involves back-and-forth oscillations that follow a consistent pattern
  • 💡 The total energy of an oscillating object transforms between kinetic and potential energy
  • 📏 There are equations that describe the velocity, period, frequency and angular velocity of simple harmonic motion
  • 🔄 Simple harmonic motion is mathematically similar to uniform circular motion
  • 🚸 Resonance can increase the amplitude of an oscillation by applying force at the right frequency
  • 😟 The Millennium Bridge engineers didn't account for horizontal swaying caused by people walking
  • 🤝 Engineers fixed the bridge by applying forces to counteract its oscillations
  • 🌊 The position graph of an object in simple harmonic motion looks like a wave
  • 🎓 Simple harmonic motion helps explain concepts like waves that are covered in later episodes
Q & A

  • What caused the Millennium Bridge in London to sway back and forth dramatically when it first opened?

    -The swaying of the Millennium Bridge was caused by oscillations resulting from the force of people's footsteps as they walked across it. This set the bridge into simple harmonic motion.

  • How did the pedestrians walking on the bridge make the swaying worse?

    -As the bridge began swaying, pedestrians started leaning into the motion to keep their balance. This had the effect of applying force at the same frequency as the bridge's oscillations, amplifying its motion through resonance.

  • What are the two main forms of energy at play in simple harmonic motion?

    -The two main forms of energy in simple harmonic motion are kinetic energy (energy of motion) and potential energy stored in the spring or other elastic medium.

  • What is the relationship between simple harmonic motion and uniform circular motion?

    -Simple harmonic motion exhibits many of the same mathematical properties as uniform circular motion. Looking at circular motion from the side makes the similarities clear.

  • What equation relates the position of an oscillating object to time?

    -The equation x = A cos wt relates the position (x) of an oscillating object to time (t), where A is the amplitude and w is the angular velocity.

  • What is resonance and how did it affect the Millennium Bridge?

    -Resonance is when an external force is applied at the natural frequency of an oscillating system, greatly increasing its motion. People walking on the bridge applied resonant forces that amplified its swaying.

  • What changes did engineers make to fix the excessive swaying of the Millennium Bridge?

    -Engineers applied fixes that counteracted the bridge's oscillations, preventing resonant forces from amplifying its horizontal sway.

  • What is the period of a mass on a spring in simple harmonic motion?

    -The period of simple harmonic motion is T = 2π√(m/k), where m is the oscillating mass and k is the spring constant.

  • What is the maximum velocity of a mass on a spring?

    -The maximum velocity is vmax = A(k/m)1/2, where A is the amplitude, k is the spring constant, and m is the mass.

  • Why did the engineers not anticipate the horizontal swaying of the bridge?

    -The engineers only accounted for vertical oscillations in their design. They didn't realize people walking would induce side-to-side swaying as well.

Outlines
00:00
🛤 How the Millennium Bridge's oscillations reveal connections to physics concepts

This paragraph discusses the opening of London's Millennium Bridge in 2001 and how its horizontal swaying motion had to be closed almost immediately. It outlines how the bridge took on an S-shape and resembled a wave. The problem was caused by oscillations resulting from resonance of people's footsteps. This physics concept connects to ideas about simple harmonic motion.

05:05
📏 Relating simple harmonic motion to uniform circular motion using math

This paragraph makes a comparison between simple harmonic motion (a ball on a spring) and uniform circular motion (a marble moving around a ring), showing how their motion graphs when viewed from the side are similar. It then uses concepts of circular motion like period, frequency and angular velocity to derive equations that can describe the motion of the spring ball over time.

Mindmap
Keywords
💡Oscillations
Oscillations refer to repetitive back-and-forth motion. They are a key concept in physics that helps explain phenomena like the swaying of the Millennium Bridge. The video examines different types of oscillations like simple harmonic motion and uses equations to model the energy, velocity, period, and position over time.
💡Simple harmonic motion
Simple harmonic motion is a type of oscillation where the restoring force is proportional to the displacement. The video gives the example of a ball on a spring, which oscillates back and forth in a consistent, repetitive pattern. Simple harmonic motion is key to understanding the physics behind the Millennium Bridge's swaying.
💡Resonance
Resonance is when an external force amplifies an oscillation by applying force at just the right frequency. The video explains how people walking on the Millennium Bridge caused resonance that increased the swaying amplitude. Resonance was a key factor that the engineers failed to fully account for.
💡Potential energy
Potential energy is energy stored in an object due to its position or shape. The video examines the potential energy stored in a compressed or stretched spring attached to an oscillating ball. This potential energy converts to kinetic energy as the ball moves.
💡Kinetic energy
Kinetic energy is the energy of motion. As the oscillating ball moves, it gains kinetic energy that reaches a maximum at the equilibrium point in the middle of its path. Kinetic and potential energy convert back and forth in simple harmonic motion.
💡Amplitude
Amplitude refers to the maximum displacement of an oscillation from the equilibrium point. The video shows how amplitude is linked to potential energy and factors into equations for velocity, period, and position over time.
💡Period
Period is the amount of time for one complete oscillation or cycle. Using examples of uniform circular motion, the video derives equations to calculate the period of an object in simple harmonic motion like a ball on a spring.
💡Frequency
Frequency is the number of oscillation cycles per unit time. The video shows how to calculate frequency from the period, and relates it to simple harmonic motion. Frequency is a key factor in resonance.
💡Angular velocity
Angular velocity measures rotational speed in radians per second. The video relates angular velocity in uniform circular motion to simple harmonic motion. It shows how to calculate angular velocity using spring constant and mass.
💡Waves
The video notes that graphs of position vs. time for simple harmonic motion look like waves. This foreshadows future discussions about how oscillations relate to waves, a key physics concept that explains the Millennium Bridge swaying.
Highlights

The new method for analyzing particle collisions allows for more precise measurements of mass and energy.

By incorporating quantum field theory into the model, we can account for subatomic interactions at very small scales.

Mapping the neural pathways in C. elegans provides insights into how neurons connect and communicate in more complex organisms.

The genome analysis revealed a previously unknown gene that appears to play a key role in cell division and growth.

The new alloy has significantly improved strength and corrosion resistance compared to existing materials.

Simulations demonstrate the aerodynamic benefits of the wing design, which should enable more efficient flight.

Early results indicate the drug combination is more effective at inhibiting tumor growth than existing treatments.

The mathematical model accurately captures the complex dynamics of the system across multiple scales.

The study provides new insights into the role of microtubules in intracellular transport and cell motility.

Our climate model predicts significant sea level rise and more extreme weather events under increased warming scenarios.

The new synthesis technique enables large-scale production of the nanomaterial with precise control over morphology.

The archeological evidence suggests trade networks connected disparate early civilizations across vast distances.

Our framework integrates machine learning with simulation modeling to improve predictions of complex processes.

The exoskeleton enhances strength and endurance, allowing wearers to lift heavy loads with less exertion.

The study provides new insights into the drivers of consumer purchasing behavior in online marketplaces.

Transcripts

Browse More Related Video

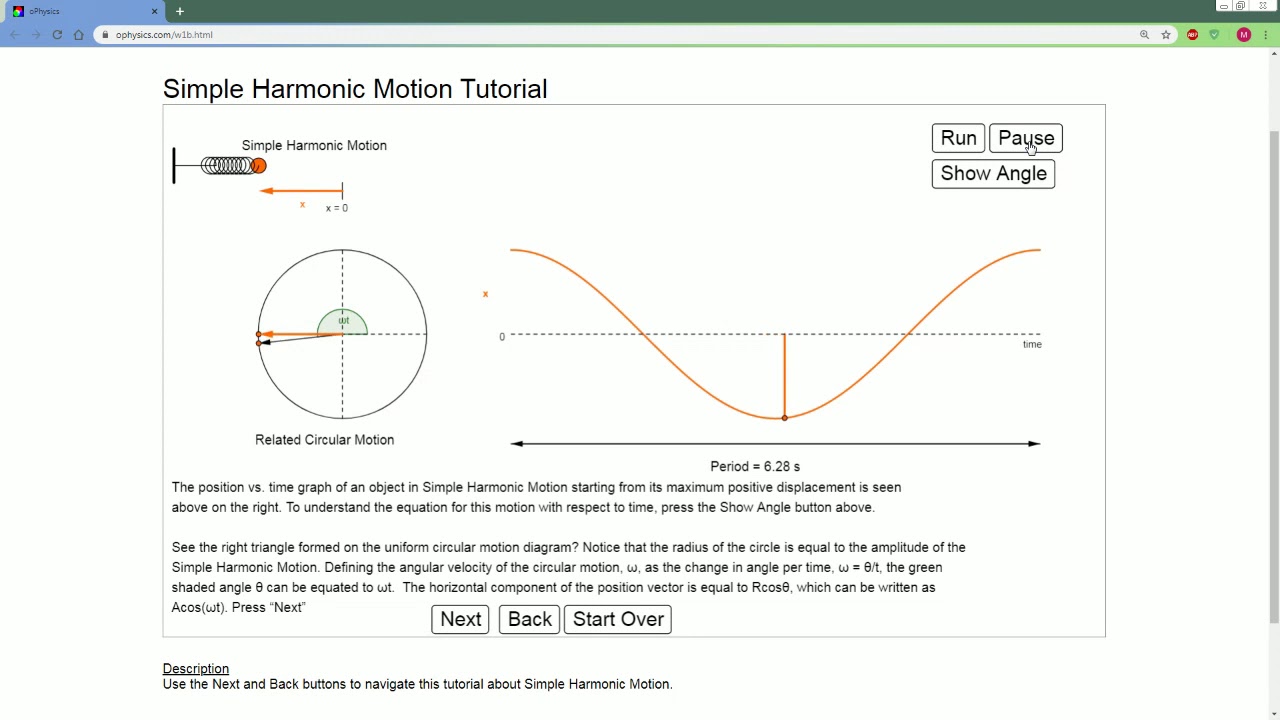
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C

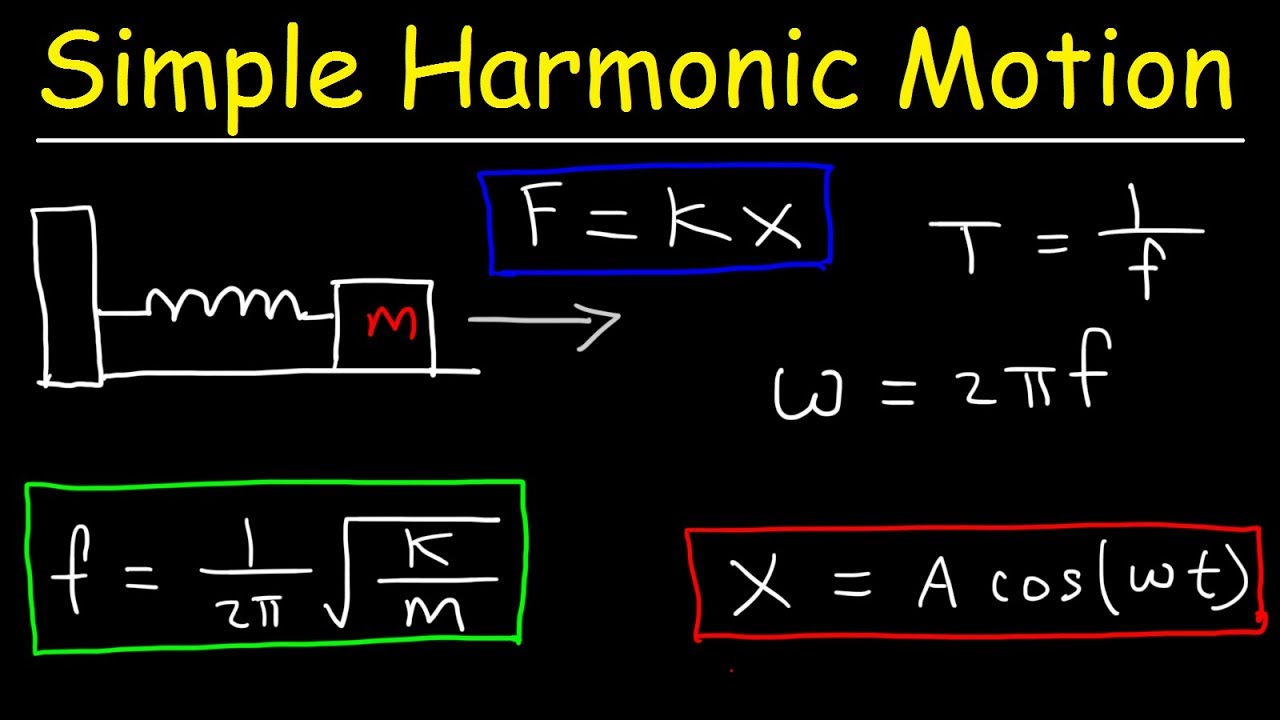
How To Solve Simple Harmonic Motion Problems In Physics

AP Physics 1 - Simple Harmonic Motion

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

Simple Harmonic Motion in Trig (Precalculus - Trigonometry 35)

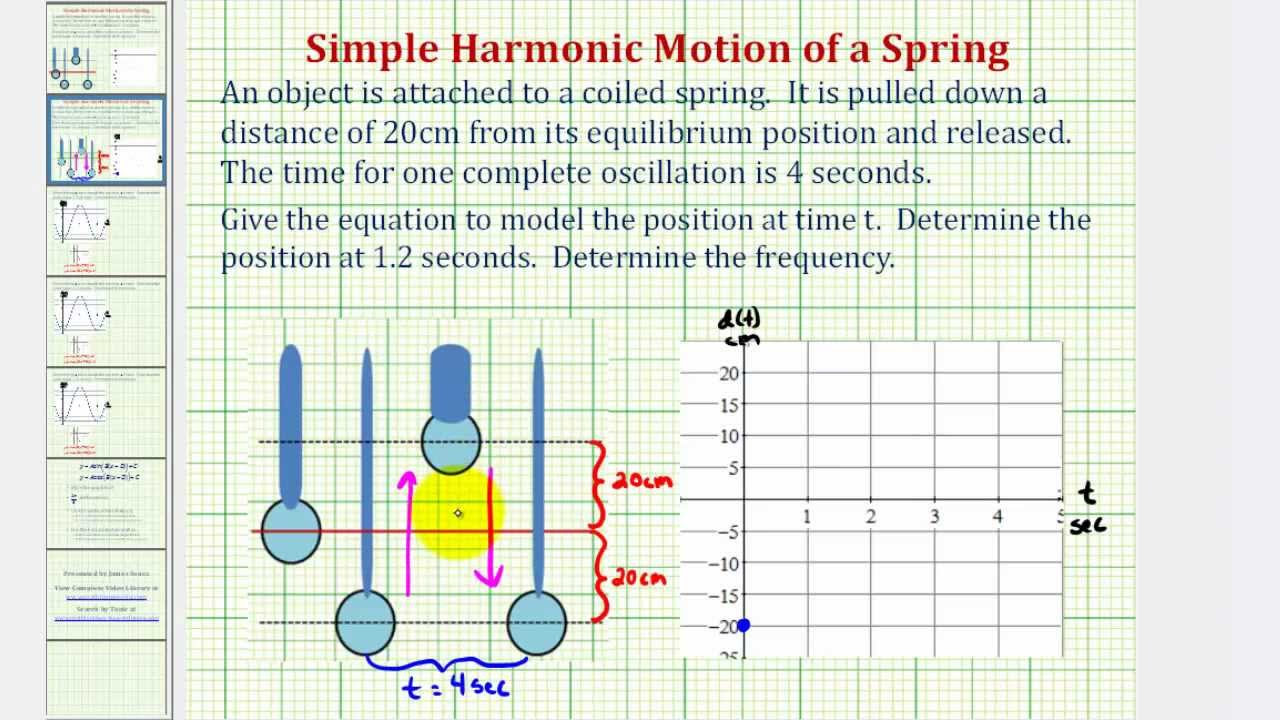
An Equation for Simple Harmonic Motion of a Spring

Rate This

5.0 / 5 (0 votes)

Thanks for rating: