Arc Length and Area of a Sector | Formulas | Sample Problems | Trigonometry | Pre-Calculus

Prof D
9 Jun 202111:59
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the host demonstrates how to calculate the arc length and the area of a sector in a circle. They introduce the formulas for both calculations, emphasizing the importance of using radians when dealing with central angles. The video proceeds with step-by-step examples, including finding arc length given a radius and central angle, determining the central angle from arc length and radius, calculating the area of a sector with a given radius and central angle, and applying these concepts to a real-world scenario involving a sprinkler system on a golf course. The host simplifies complex mathematical concepts, making them accessible to viewers and encouraging engagement through comments.

Takeaways
  • 📚 The video is an educational tutorial on calculating the arc length and the area of a sector in a circle.
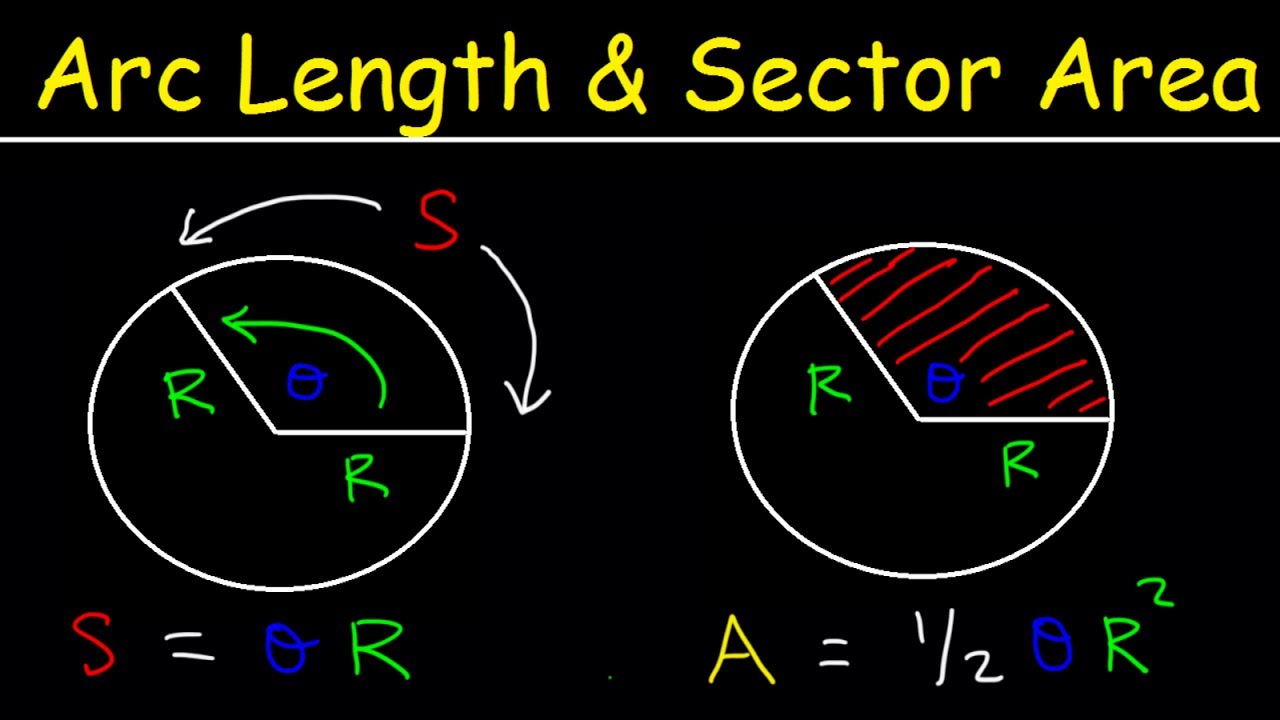
  • 📐 The formula for arc length (s) is s = r × θ, where r is the radius and θ is the central angle in radians.
  • 🔍 To convert degrees to radians, multiply the degree measure by π over 180.
  • 📏 The formula for the area (A) of a sector is A = ½ × r² × θ, with θ in radians.
  • 🎯 Example 1: The length of an arc with a radius of 10 meters and a central angle of 30 degrees is calculated by converting degrees to radians and applying the arc length formula.
  • 🧩 Example 2: To find the central angle given the arc length and radius, rearrange the arc length formula and solve for θ.
  • 📏 Example 3: The area of a sector with a central angle of 60 degrees and a radius of 3 meters is found by converting degrees to radians and using the area formula.
  • 🌐 Example 4: The area watered by a sprinkler with a 70 feet radius and a 120-degree angle is calculated similarly, converting degrees to radians and applying the area formula.
  • 📈 The video demonstrates the process of converting between degrees and radians, which is essential for solving problems involving circles.
  • 📝 The examples provided in the video illustrate the practical application of the formulas for arc length and sector area.
  • 👨‍🏫 The presenter, Prof D, encourages viewers to ask questions or seek clarifications in the comments section.
Q & A

  • What is the formula for calculating the arc length of a circle?

    -The formula for calculating the arc length (s) of a circle is s = r * θ, where r is the radius of the circle and θ is the central angle in radians.

  • How do you convert degrees to radians for the arc length formula?

    -To convert degrees to radians, you multiply the degree measure by π/180. For example, 30 degrees is equivalent to 30 * π/180 radians.

  • What is the formula for finding the area of a sector of a circle?

    -The formula for finding the area (A) of a sector of a circle is A = 1/2 * r^2 * θ, where r is the radius and θ is the central angle in radians.

  • How can you find the central angle if you know the arc length and the radius of the circle?

    -To find the central angle when you know the arc length (s) and the radius (r), you rearrange the arc length formula to θ = s / r.

  • In the first example, what is the radius of the circle and what central angle is used?

    -In the first example, the radius of the circle is 10 meters, and the central angle used is 30 degrees.

  • What is the result of the first example's arc length calculation?

    -The result of the first example's arc length calculation is 5π/3 meters, which simplifies to approximately 5.23 meters.

  • In the second example, how do you find the measure of the central angle given the arc length and radius?

    -In the second example, to find the measure of the central angle, you divide the arc length by the radius and then multiply by 180/π to convert from radians to degrees.

  • What is the area of the sector in the third example with a central angle of 60 degrees and a radius of 3 meters?

    -The area of the sector in the third example is 9π/2 square meters, which is approximately 14.13 square meters when π is approximated as 3.1416.

  • In the fourth example, how is the area of the fairway watered by the sprinkler calculated?

    -In the fourth example, the area of the fairway watered by the sprinkler is calculated using the sector area formula with a central angle of 120 degrees and a radius of 70 feet.

  • What is the approximate area of the fairway watered by the sprinkler in the fourth example?

    -The approximate area of the fairway watered by the sprinkler in the fourth example is 5131.28 square feet.

Outlines
00:00
📚 Introduction to Arc Length and Sector Area Calculations

This paragraph introduces the topic of the video, which is about calculating the arc length and the area of a sector in a circle. The presenter explains the formulas for both calculations: the arc length (s) is given by the formula s = r * θ, where r is the radius and θ is the central angle in radians, and the area (a) of a sector is given by a = 0.5 * r^2 * θ. The paragraph also emphasizes the importance of converting angle measures from degrees to radians when necessary. The presenter then proceeds to work through an example problem involving a circle with a radius of 10 meters and a central angle of 30 degrees, demonstrating the application of the formulas.

05:03
🔍 Examples of Calculating Arc Length and Sector Area

In this paragraph, the presenter continues with more examples to illustrate the application of the formulas for arc length and sector area. The second example involves finding the central angle of a circle with a radius of four meters given an arc length of six meters. The presenter shows the process of solving for the angle using the arc length formula and converting the result back into degrees. The third example calculates the area of a sector with a central angle of 60 degrees and a radius of three meters. The presenter demonstrates the conversion of degrees to radians, applies the area formula, and simplifies the result to find the area in square meters. The example concludes with an approximate decimal value for the area using the value of pi as 3.1416.

10:06
🌳 Real-World Application: Sprinkler System on a Golf Course

The final paragraph presents a real-world application of the formulas discussed in the video. It describes a scenario where a sprinkler on a golf course sprays water over a distance of 70 feet and rotates through an angle of 120 degrees. The presenter aims to find the area of the fairway watered by the sprinkler. The process involves converting the angle from degrees to radians, calculating the area using the sector area formula with the given radius and central angle, and then converting the result into a decimal form using the value of pi as 3.14. The final result is an approximation of the watered area in square feet, providing a practical example of how these mathematical concepts can be applied to everyday problems.

Mindmap
Keywords
💡Arc Length
Arc length refers to the distance measured along the curved line forming part of the circumference of a circle. In the video, it is calculated using the formula s = r * theta, where 'r' is the radius and 'theta' is the central angle in radians. This concept is essential for understanding how to measure parts of a circle's perimeter.
💡Sector Area
Sector area is the area of a section of a circle, bounded by two radii and the arc between them. The formula for the area of a sector is A = 1/2 * r^2 * theta, where 'r' is the radius and 'theta' is the central angle in radians. This concept helps in finding the region covered by a specific angle in a circle.
💡Radius
The radius of a circle is the distance from the center of the circle to any point on its circumference. It is a crucial value in the formulas for both arc length and sector area. The script provides examples with different radii, such as 10 meters and 4 meters, to demonstrate these calculations.
💡Central Angle
A central angle is an angle whose vertex is the center of the circle and whose sides are radii. It is measured in degrees or radians. The video script explains how to convert degrees to radians and uses central angles to find arc lengths and sector areas, such as converting 30 degrees to radians for an arc length calculation.
💡Radians
Radians are a unit of angular measure used in many areas of mathematics. One radian is the angle created when the radius is wrapped around the circle's circumference. The script emphasizes converting degrees to radians (e.g., 30 degrees to pi/6 radians) to use in formulas for arc length and sector area.
💡Conversion
Conversion in this context refers to changing angles from degrees to radians, necessary for using the formulas for arc length and sector area. The script explains this process by multiplying degrees by pi/180, showing step-by-step calculations for accurate results.
💡Example Problems
Example problems are used throughout the video to illustrate how to apply mathematical formulas to real-world scenarios. These examples help viewers understand the process of calculating arc length and sector area, providing practical applications of the discussed concepts.
💡Formula
Formulas are mathematical equations used to calculate arc length (s = r * theta) and sector area (A = 1/2 * r^2 * theta). The video script repeatedly uses these formulas, explaining each component and demonstrating their application through examples.
💡Theta
Theta (θ) represents the central angle in radians within the formulas for arc length and sector area. The script includes several instances of converting central angles from degrees to radians (e.g., 30 degrees to pi/6) to use in these calculations.
💡Sprinkler Problem
The sprinkler problem in the video is an example used to apply the formula for the area of a sector. It involves a sprinkler rotating through an angle of 120 degrees, spraying water over a radius of 70 feet, and calculating the area watered. This real-world example helps contextualize the mathematical concepts discussed.
Highlights

Introduction to the video on finding arc length and sector area in a circle.

Formula for arc length: s = r * θ, where θ is in radians.

Formula for sector area: A = 0.5 * r^2 * θ, with θ in radians.

Conversion of angle measure from degrees to radians.

Example 1: Finding arc length with a 10m radius and 30-degree angle.

Conversion of 30 degrees to radians (π/6) for arc length calculation.

Result of Example 1: Arc length is 5π/3 meters.

Example 2: Finding central angle given arc length and radius.

Solving for θ when arc length (s) is 6m and radius (r) is 4m.

Result of Example 2: Central angle is 3/2 radians.

Example 3: Calculating sector area with a 60-degree angle and 3m radius.

Conversion of 60 degrees to radians (π/3) for sector area calculation.

Result of Example 3: Sector area is 9π/2 square meters.

Approximation of π to 3.1416 for decimal conversion.

Example 4: Sprinkler on a golf course spraying a 70-foot radius at 120 degrees.

Conversion of 120 degrees to radians (2π/3) for area calculation.

Result of Example 4: Area watered by the sprinkler is approximately 5131.28 square feet.

End of the video with a summary and invitation for questions or clarifications.

Transcripts

Browse More Related Video

Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry

Radians and Degrees

AP Physics Workbook 7.A Relationship between Arc Length and Angle of Rotation

Area of a Sector, Angular Velocity, Applications (Precalculus - Trigonometry 5)

Introduction to Radians (Precalculus - Trigonometry 3)

Trig 0.1 - Angles, Degrees and Radians

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsGeometryArc LengthSector AreaEducationalCalculationCircle FormulasMath TutorialProblem SolvingTrigonometryPi Calculation