Trigonometry - What Exactly Is a Radian?

The Organic Chemistry Tutor
15 Jan 202012:05
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the concept of radians, a unit of angle measurement equivalent to approximately 57.3 degrees. It explains the relationship between radians and the circle's circumference, illustrating that a full circle encompasses 2π radians or 360 degrees. The script further clarifies the derivation of radians from the arc length being equal to the circle's radius and provides formulas for converting between radians and degrees, enhancing understanding of this fundamental angle measure in mathematics.

Takeaways
  • 📏 A Radian is a unit of angle measure, equivalent to approximately 57.3 degrees.
  • 🔄 The full rotation of a circle is 360 degrees, which is also equal to 2π radians.
  • 🧮 To convert radians to degrees, divide 360 degrees by 2π, resulting in approximately 57.29577951 degrees per radian, which rounds to 57.3 degrees.
  • 📐 The concept of a radian comes from the arc length of a circle being equal to its radius, creating an angle of 1 radian.
  • 📉 The formula for the arc length (s) in relation to the radius (r) and angle in radians (θ) is s = r * θ.
  • 🔄 To find the arc length when the angle is given in radians, set the arc length equal to the radius (s = r), resulting in an angle of 1 radian.
  • 🔢 The units of the angle in radians (θ) and the radius (r) will cancel out, leaving the arc length (s) in the unit of the radius.
  • 🌀 The circumference of a circle is 2π times the radius, which is the total arc length for a full circle of 2π radians or 360 degrees.
  • ↔️ To convert degrees to radians, multiply the degree measure by π/180.
  • ↔️ To convert radians to degrees, multiply the radian measure by 180/π.
  • 🤓 Understanding radians is essential for advanced mathematics and physics, especially when dealing with circular motion and trigonometric functions.
Q & A

  • What is a radian?

    -A radian is a unit of angle measure, where one radian is equal to an angle measure of approximately 57.3 degrees.

  • How can you derive the value of one radian in degrees?

    -You can derive the value of one radian in degrees by dividing 360 degrees by 2π, which gives you approximately 57.3 degrees.

  • What is the relationship between a full circle and radians?

    -A full circle is equal to 360 degrees, which is also equivalent to 2π radians.

  • How is the value of π used in the context of radians?

    -The value of π, approximately 3.14159265, is used in the equation to convert degrees to radians by dividing 360 degrees by 2π.

  • What is the definition of the arc length in the context of a circle?

    -The arc length is the distance along the circumference of a circle between two points, and it is represented by the symbol 's' in the script.

  • How does the arc length relate to the angle measure and the radius of a circle?

    -The arc length is equal to the angle measure times the radius of the circle, as per the formula s = θ * R.

  • What is the significance of one radian in terms of arc length and radius?

    -One radian occurs when the arc length is equal to the radius of the circle, which is a fundamental concept in understanding radians.

  • How can you convert an angle measure from degrees to radians?

    -To convert degrees to radians, multiply the angle in degrees by π and then divide by 180.

  • What is the total number of radians in a complete circle?

    -A complete circle has an angle measure of 2π radians, which is approximately 6.283 radians.

  • How can you convert an angle measure from radians to degrees?

    -To convert radians to degrees, multiply the angle in radians by 180 and then divide by π.

  • What is the practical application of understanding radians in geometry?

    -Understanding radians is crucial in geometry for calculating arc lengths, areas of sectors, and for various trigonometric functions that operate in the radian mode.

Outlines
00:00
📏 Understanding Radians: The Basics

This paragraph introduces the concept of a radian, defining it as a unit of angle measurement equal to approximately 57.3 degrees. It explains how the value of one radian is derived from the full circle angle of 360 degrees, which is equivalent to 2π radians. The explanation includes a step-by-step calculation to show how dividing 360 degrees by 2π yields the radian's value. It also touches on the geometric interpretation of a radian, describing it as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle.

05:01
🔍 Deep Dive into Radians and Their Applications

The second paragraph delves deeper into the concept of radians, discussing the relationship between the radius of a circle and the arc length it subtends. It uses the formula s = rθ to explain how the arc length (s) is calculated when the angle (θ) is measured in radians. The paragraph provides an example with a circle having a radius of 4 inches to illustrate how to find the arc length when the angle is given in radians. It also addresses the question of how many radians are in a full circle, explaining that a complete circle encompasses 2π radians or 360 degrees. Additionally, it introduces the process of converting between radians and degrees, providing formulas and examples for both conversions.

10:02
🔄 Conversion Between Radians and Degrees

The final paragraph focuses on the conversion between radians and degrees, providing clear instructions and examples. It explains how to convert an angle from degrees to radians by multiplying the degree measure by π/180. The paragraph simplifies the conversion process with examples, such as converting 30 degrees and 60 degrees to radians. It also covers the reverse conversion, changing radians to degrees by multiplying the radian measure by 180/π. The examples given include converting 5π/6 and 4π/3 radians to degrees, demonstrating the straightforward process of unit conversion between these two angular measurements.

Mindmap
Keywords
💡Radian
A radian is a unit of angle measure that is defined as the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. In the video, it is explained that one radian is approximately equal to 57.3 degrees. The concept is central to the video's theme, as it is the fundamental unit for measuring angles in a circle, particularly in the context of mathematics and physics.
💡Angle Measure
Angle measure refers to the size or magnitude of an angle, typically expressed in degrees or radians. In the video, the concept is used to explain the relationship between radians and degrees, and how to convert between these two units of measurement. The video emphasizes that a full circle is 360 degrees, which is equivalent to 2π radians, providing the basis for understanding the radian as an angle measure.
💡Circle
A circle is a geometric shape consisting of all points equidistant from a given point, known as the center. The video script uses the circle to illustrate the concept of radians, explaining that a full rotation around the circle is 360 degrees or 2π radians. The circle serves as a practical example to demonstrate the relationship between the arc length and the angle measure in radians.
💡Arc Length
Arc length is the distance along the curved line that makes up a part of the circumference of a circle. In the video, the arc length is equated to the radius of the circle when the angle measure is one radian. This relationship is crucial in understanding how radians are derived from the physical properties of a circle.
💡Radius
The radius of a circle is the distance from the center to any point on the circumference. The video explains that when the arc length is equal to the radius, the angle measure is one radian. The radius is also used to calculate the arc length for different angle measures in radians, as shown in the script's examples.
💡Circumference
Circumference refers to the total distance around a circle. The video script states that the circumference is equal to 2π times the radius of the circle. This equation is derived from the arc length formula and is used to explain that a full circle encompasses an angle measure of 2π radians.
💡PI (π)
PI, often represented by the symbol π, is a mathematical constant that represents the ratio of a circle's circumference to its diameter. In the video, π is used to establish the relationship between radians and degrees, and to calculate the number of radians in a full circle. The script also mentions the approximate value of π as 3.14, which is used in calculations.
💡Degrees
Degrees are a unit of measurement for angles, where a full circle is divided into 360 equal parts. The video script explains how to convert degrees to radians and vice versa, using the relationship that 180 degrees is equivalent to π radians. Degrees are a common unit of angle measurement in everyday contexts outside of the radian's more technical use.
💡Conversion
Conversion in the context of the video refers to the process of changing an angle's measurement from degrees to radians or vice versa. The script provides formulas and examples for converting between these two units, which is essential for understanding how the two systems of angle measurement relate to each other.
💡Unit of Measure
A unit of measure is a standard used to express the magnitude of a physical quantity. In the video, the radian is introduced as a specific unit for measuring angles, distinct from the more familiar degree. The script explains how radians are derived from the properties of a circle and how they can be used in place of degrees in certain mathematical contexts.
Highlights

A Radian is a unit of angle measure.

One Radian is approximately equal to 57.3 degrees.

A full circle is 360 degrees, which is also equal to 2π radians.

To find the angle measure of one Radian in degrees, divide 360 by 2π.

The value of π is approximately 3.14159265.

Using π in the equation 360/2π gives approximately 57.29577951 degrees.

The concept of a Radian comes from the arc length being equal to the radius of the circle.

When the arc length equals the radius, the angle is 1 Radian.

The formula for the arc length is s = θ * R, where s is the arc length, θ is the angle in radians, and R is the radius.

The circumference of a circle is 2π times the radius.

A complete circle has an angle measure of 2π radians or 360 degrees.

To convert degrees to radians, multiply the angle in degrees by π/180.

For example, 30 degrees is equal to π/6 radians.

To convert radians to degrees, multiply the angle in radians by 180/π.

For instance, 5π/6 radians is equal to 150 degrees.

4π/3 radians is equivalent to 240 degrees.

The video explains the concept, origin, and conversion between radians and degrees.

Transcripts

Browse More Related Video

Converting Radians and Degrees (Precalculus - Trigonometry 4)

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

Trig 0.1 - Angles, Degrees and Radians

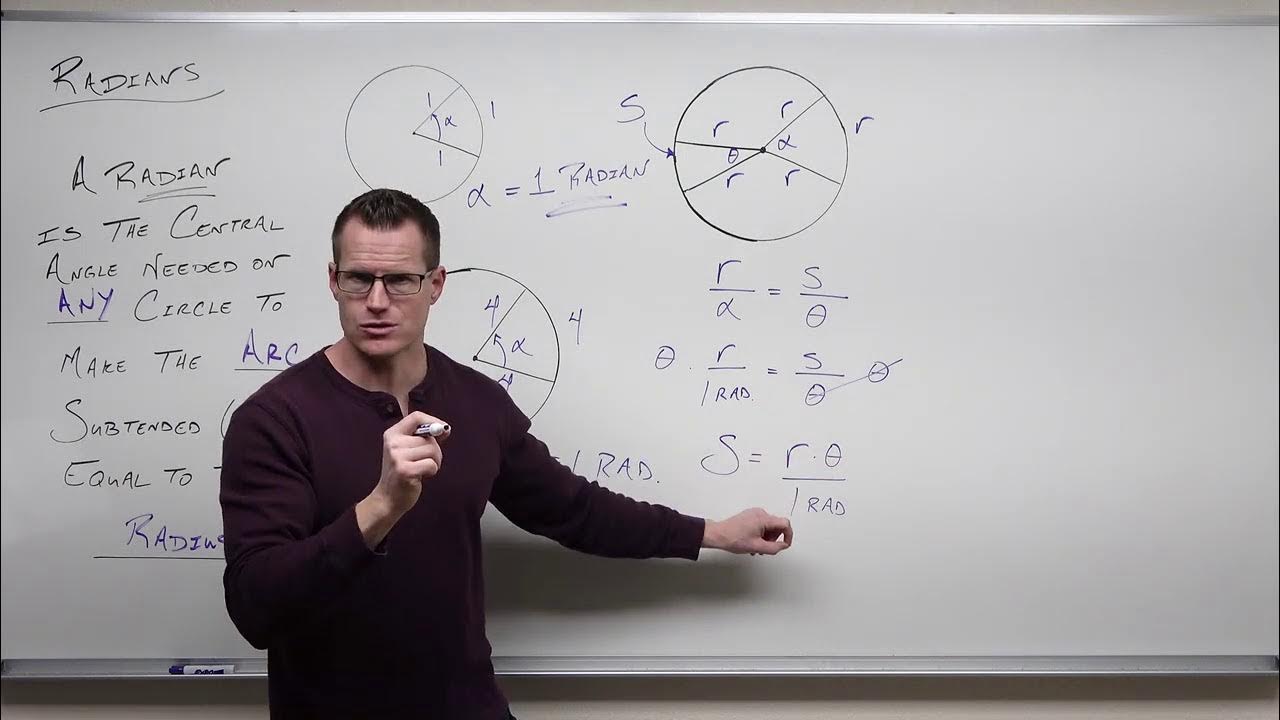
Introduction to Radians (Precalculus - Trigonometry 3)

Introduction to Trigonometry: Angles and Radians

What are radians? Simply explained

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
RadiansDegreesMathematicsAngle MeasureEducationalConversionCircle GeometryTrigonometryArc LengthUnit Conversion