Introduction to Radians (Precalculus - Trigonometry 3)

Professor Leonard
9 Feb 202117:25
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides an in-depth explanation of radians, contrasting them with degrees and delving into their mathematical foundation. It explains that a radian is an angular measurement derived from the relationship between a circle's radius and an arc length equal to that radius. The script emphasizes that radians are consistent across circles of different sizes, similar to degrees, but are measured differently. It also introduces the concept of using radians to determine arc length with the formula s = rθ, where s is the arc length, r is the radius, and θ is the angle in radians. The importance of using radians, rather than degrees, in this context is highlighted, as the formula is based on the specific unit of measurement for radians. The script concludes with practical examples of calculating arc length from angles and vice versa, reinforcing the concept's utility in mathematical applications, particularly in calculus.

Takeaways
  • 📏 A radian is a measure of angle that represents the angular relationship where the arc length of a circle is equal to the length of the radius.
  • 🔄 Radians are used regardless of the circle's size, maintaining the same relationship between the radius and the arc length it subtends.
  • 🔵 The concept of a radian is distinct from degrees, which measure angles as a fraction of a full circle (360 degrees).
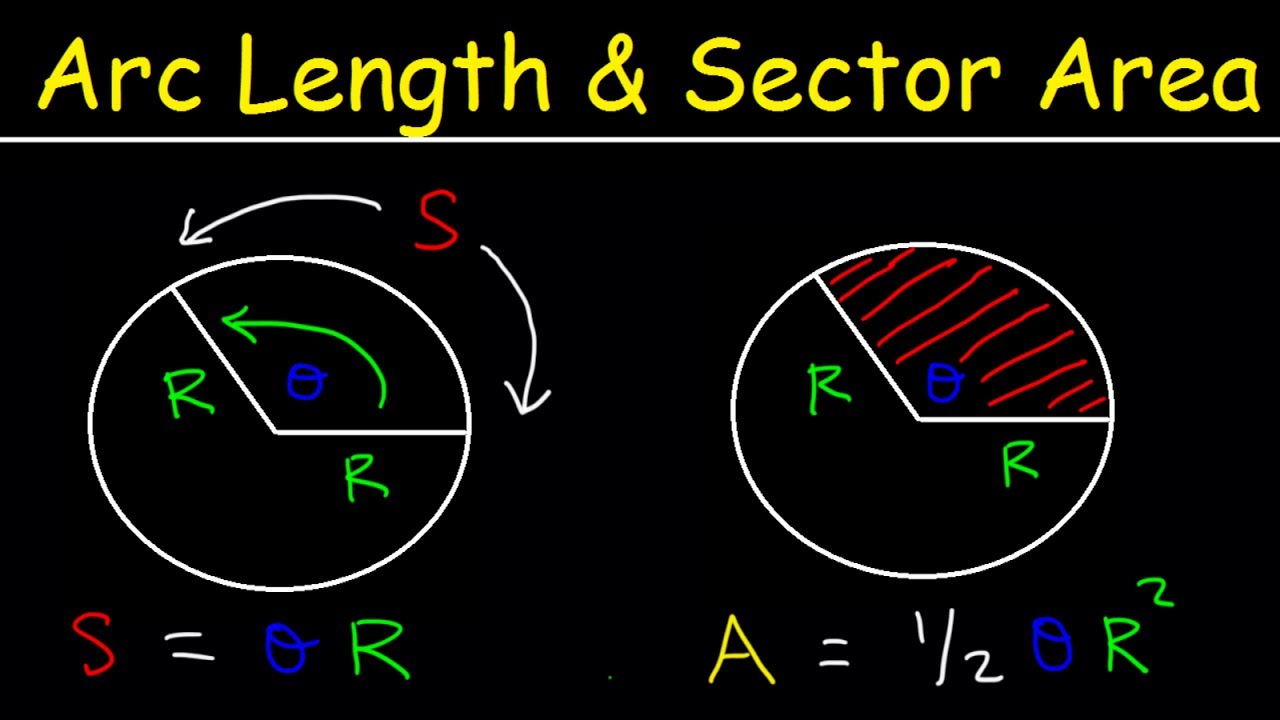
  • 📐 The formula for the arc length (s) in terms of radius (r) and angle in radians (θ) is s = r * θ, and it only works for angles measured in radians.
  • ⚖️ When using the arc length formula, the units for radius and arc length must be consistent, and the angle must be specified in radians for the formula to be valid.
  • 🤔 To find the arc length for an angle not equal to one radian, a proportion can be used based on the definition of a radian.
  • 🧮 The size of one radian remains constant and does not change with the size of the circle; it is the ratio between the radius and the arc length that defines it.
  • 📉 If the arc length is less than the radius, the angle in radians is less than one radian, and vice versa.
  • 🔢 radians are commonly used in calculus and many mathematical formulas that involve angles and are preferred for their simplicity in certain contexts.
  • 🔄 Understanding the concept of radians is crucial for converting between degrees and radians, which will be covered in the next video.
  • ⚠️ Students often mistakenly apply the arc length formula to degrees because they are not aware that it strictly applies to radians.
Q & A

  • What is the definition of a radian?

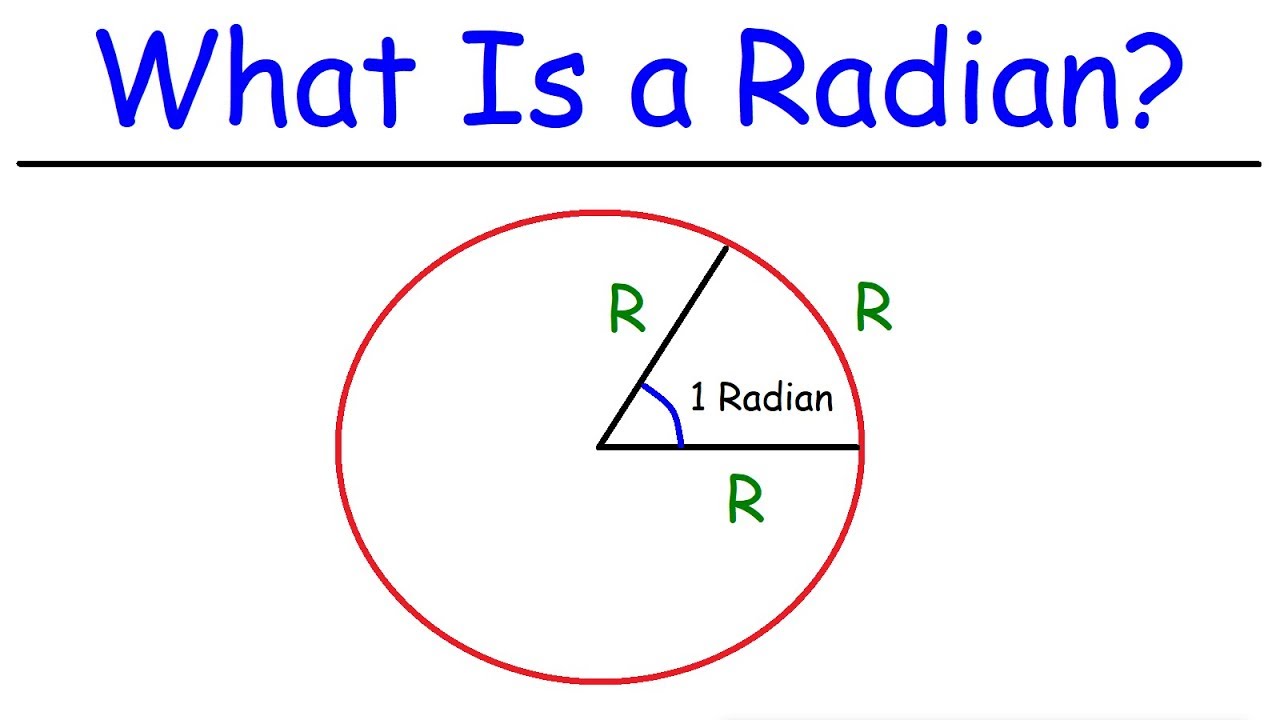
    -A radian is an angular relationship between a radius and an arc length that is equal to that radius. It is the central angle needed on any circle to make the arc subtended by two radii equal to the radius.

  • How is a radian different from a degree?

    -A radian is a measure of angle based on the ratio of the arc length to the radius of a circle, whereas a degree is a measure of angle that represents 1/360th of a full circle or rotation.

  • What is the relationship between the radius, arc length, and angle in radians?

    -The relationship is such that the arc length is equal to the radius when the angle at the center of the circle is one radian. This relationship holds true for any circle, regardless of its size.

  • Why is the formula s = r * theta only valid for radians?

    -The formula s = r * theta is derived from the definition of a radian, which involves the arc length being equal to the radius. This relationship is specific to radians and does not hold for degrees because the units of radians and the arc length are inherently linked in the definition.

  • How can you find the arc length given an angle measured in radians?

    -You can find the arc length by multiplying the radius of the circle by the angle in radians. The formula for this is s = r * theta, where s is the arc length, r is the radius, and theta is the angle in radians.

  • How can you find the central angle given an arc length and radius?

    -You can find the central angle by dividing the arc length by the radius. The formula for this is theta = s / r, where theta is the angle in radians, s is the arc length, and r is the radius.

  • Why is it important to specify 'radians' when using the formula s = r * theta?

    -Specifying 'radians' is important because the formula is based on the definition of a radian. Omitting the unit can lead to confusion and errors, as the formula does not apply to degrees.

  • What is a unit circle?

    -A unit circle is a circle with a radius of one. It is used as a reference to define angles in radians without concern for the units of measurement.

  • Why is the concept of radians fundamental in calculus and trigonometry?

    -Radians are fundamental because they provide a natural way to relate the size of an angle to the length of the arc it subtends on a circle, which is essential in calculus for dealing with derivatives and integrals involving trigonometric functions.

  • How does the understanding of radians help in converting between degrees and radians?

    -Understanding radians allows you to appreciate the different units of angular measurement and their relationship. It enables you to convert between degrees and radians using the fact that 180 degrees is equivalent to π radians.

  • What is the significance of the radian measure in the context of an equilateral triangle?

    -In the context of an equilateral triangle inscribed in a circle, the central angle that corresponds to the base of the triangle (which is twice the radius) is 1 radian. This is because the arc length subtended by the base is equal to the radius, and the central angle is 60 degrees (or π/3 radians), which is one-third of a full circle (360 degrees or 2π radians).

Outlines
00:00
📐 Understanding Radians and Their Relationship to Circles

This paragraph introduces the concept of radians as a measure of angles, distinct from degrees. It explains that a radian is defined by the central angle of a circle that intercepts an arc whose length is equal to the radius of the circle. The importance of understanding the relationship between the radius, arc length, and the angle is emphasized. The paragraph also clarifies that the size of one radian remains constant regardless of the circle's size, and it is used as a unit of measurement for angles in a circle, similar to degrees but measured differently.

05:01
🔍 Calculating Arc Length with Radians

The second paragraph delves into how to determine the arc length associated with a given angle in radians. It establishes that if the angle is one radian, the arc length will be equal to the radius. For angles that are not exactly one radian, a proportion is used to find the arc length. The paragraph also discusses the formula for arc length, which is s = r * theta, where s is the arc length, r is the radius, and theta is the angle in radians. It is emphasized that this formula is only valid for radians, not degrees, due to the units of measurement involved.

10:02
📚 Recap and Application of Radian Concepts

This paragraph serves as a recap, reinforcing the concept that radians measure angles differently from degrees. It reiterates the definition of a radian and the formula for arc length using radians. The paragraph also provides an example of calculating the arc length given a radius and an angle in radians. It further explains that the formula assumes the angle is measured in radians, which is why the radian unit is often omitted in practice. The paragraph concludes with an example calculation, demonstrating how to find the arc length when given the radius and the angle in radians.

15:04
🔢 Finding Central Angles from Arc Lengths

The final paragraph focuses on calculating the central angle given the arc length and radius, using the formula derived from the radian concept. It provides an example with a radius of 12 meters and an arc length of 16 meters, showing how to find the central angle in radians. The paragraph clarifies that angles resulting from formulas that only work with radians are indeed in terms of radians, even if the radian unit is not explicitly written. It concludes with a teaser for the next video, which will cover the conversion between degrees and radians.

Mindmap
Keywords
💡Radians
Radians are a unit of angular measure used in mathematics. Unlike degrees, which divide a circle into 360 parts, radians are based on the relationship between the length of an arc and the radius of a circle. In the video, it is explained that one radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle. This concept is central to understanding the video's theme of angular measurements and their application in mathematics.
💡Degrees
Degrees are a common unit of measure for angles, dividing a full circle into 360 equal parts. The video contrasts degrees with radians, emphasizing that while both measure angles, they do so in fundamentally different ways. Degrees are mentioned to highlight the distinction and to prepare for the conversion between degrees and radians, which is a topic for the subsequent video.
💡Arc Length
Arc length refers to the distance along the circumference of a circle between two points. In the context of the video, arc length is crucial for defining a radian. It is used to describe the portion of the circle that is 'cut' by a central angle when the length of this arc is equal to the radius of the circle, thus forming an angle of one radian.
💡Central Angle
A central angle is an angle whose vertex is at the center of a circle. The video uses the concept of a central angle to explain how radians are formed. Specifically, a radian is defined as a central angle that, when drawn in a circle, subtends an arc whose length is equal to the length of the radius of the circle.
💡Unit Circle
A unit circle is a circle with a radius of one unit. It serves as a reference for understanding angles in terms of radians. The video mentions the unit circle to illustrate that regardless of the size of the circle, one radian always represents the same angular relationship, just as one degree does in the degree system.
💡Proportion
Proportion is a mathematical concept that describes the relationship of two ratios being equivalent. In the video, the concept of proportion is used to derive the formula for the arc length in terms of the radius and the angle in radians. It is a fundamental principle that allows the calculation of arc lengths for different radii and angles, as long as the angle is measured in radians.
💡Formula
A formula in mathematics is an expression that shows the relationship between certain quantities. The video introduces the formula for calculating the arc length in terms of the radius (r) and the angle in radians (θ), which is s = r * θ. This formula is essential for the video's discussion on radian measures and is repeatedly emphasized to only apply to radians, not degrees.
💡Unit Conversion
Unit conversion is the process of converting a quantity from one unit of measurement to another. The video touches on the importance of unit conversion, particularly when using the arc length formula. It stresses that the formula s = r * θ only works when the angle θ is measured in radians, and converting to degrees would lead to incorrect results.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. The video mentions trigonometry in the context of using radians, as most trigonometric functions and calculus applications are typically expressed in terms of radians rather than degrees.
💡Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. The video briefly mentions calculus to highlight that radians are predominantly used in this field, especially when dealing with functions that involve circles or periodic phenomena, such as trigonometric functions.
💡Conversion between Degrees and Radians
The process of converting between degrees and radians is an important skill in mathematics, particularly when transitioning between different mathematical contexts or applications. The video script alludes to this process as a topic for the next video, emphasizing the need to understand both systems of angular measurement for comprehensive mathematical understanding.
Highlights

A radian is an angular relationship between a radius and an arc length that's equal to that radius.

One radian is the same on any circle, regardless of its size.

A radian is a central angle that makes the arc subtended by two radii equal to the radius.

A unit circle is a circle with a radius of one, which is used to simplify calculations involving radians.

The size of one radian never changes; it's the relationship between the radius and arc length that defines it.

The formula for arc length, s = r * theta, only works for radians and not for degrees.

Radians are used extensively in calculus and many mathematical formulas.

Understanding the relationship between radians and the circle's radius is crucial for using radian-based formulas.

The central angle theta in radians can be calculated from the arc length and radius using the formula theta = s / r.

A central angle of one-third radian will create an arc length that is one-third of the radius.

An arc length greater than the radius implies the central angle is more than one radian.

The concept of radians is fundamental to understanding more complex mathematical operations involving angles and circles.

Radian measurements are essential for accurately calculating arc lengths and central angles in mathematical problems.

The video emphasizes the importance of not confusing radians with degrees when using mathematical formulas.

Students often make the mistake of using the arc length formula with degrees instead of radians.

The video provides a clear explanation of the concept of radians, which is essential for further study in calculus and trigonometry.

The upcoming video will cover how to convert between degrees and radians, which is a critical skill in mathematics.

Transcripts

Browse More Related Video

Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry

Radians and Degrees

Converting Radians and Degrees (Precalculus - Trigonometry 4)

Trigonometry - What Exactly Is a Radian?

Trig 0.1 - Angles, Degrees and Radians

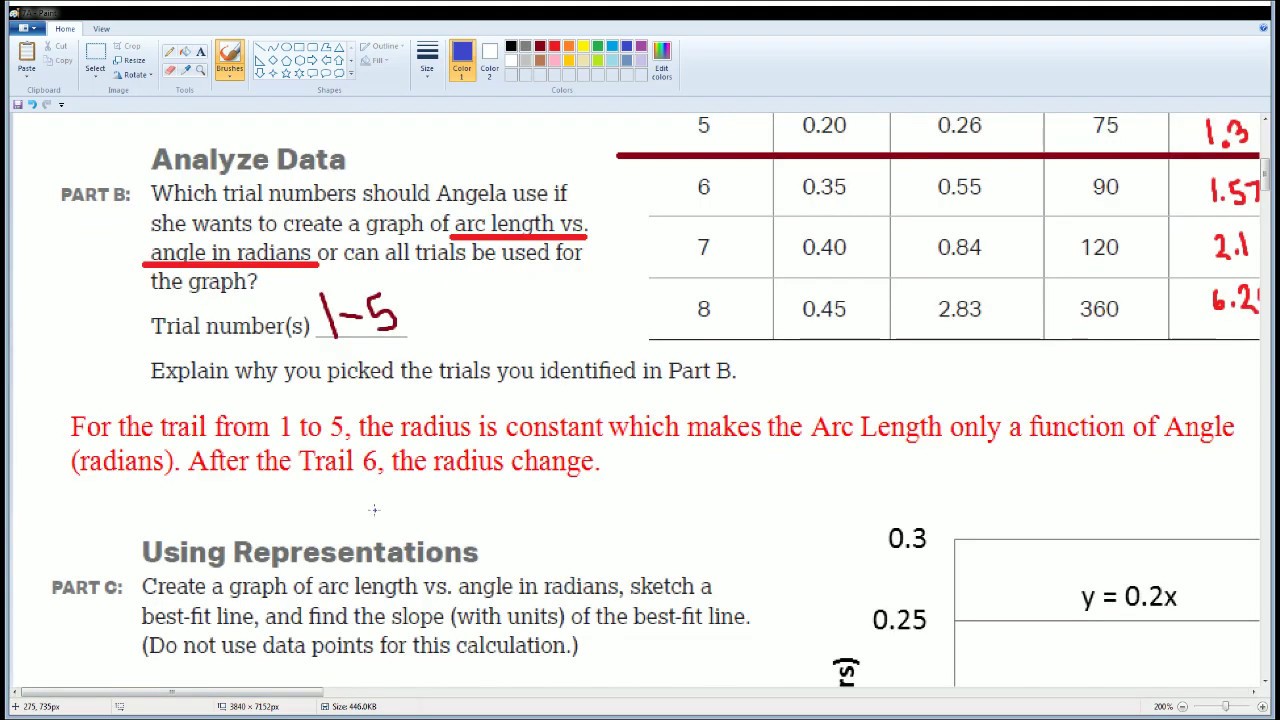
AP Physics Workbook 7.A Relationship between Arc Length and Angle of Rotation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
RadiansDegreesMathematicsConversionTrigonometryCircle GeometryUnit CircleArc LengthCentral AngleCalculus