The Physics of Music: Crash Course Physics #19
TLDRThis video explains the science behind how musical instruments like guitars, pianos, and flutes produce different notes through standing sound waves. It discusses how the fundamental frequencies and overtones of standing waves relate to musical notes. It also explains why the harmonics sound different on instruments like flutes versus clarinets - flutes can't produce even harmonics since their pipes only cover a quarter wavelength. Overall, the physics of how wavelength, frequency, velocity, and pipe ends determine an instrument's unique harmonics and sound is explored.
Takeaways
- 😀 Sound is created by longitudinal waves that cause a medium to oscillate back and forth
- 👂 Musical instruments use standing waves that have fixed nodes and oscillating antinodes
- 🎸 Standing waves are created by interference of reflected waves in strings/pipes
- 🎹 The fundamental wave is the 1st harmonic; higher harmonics are called overtones
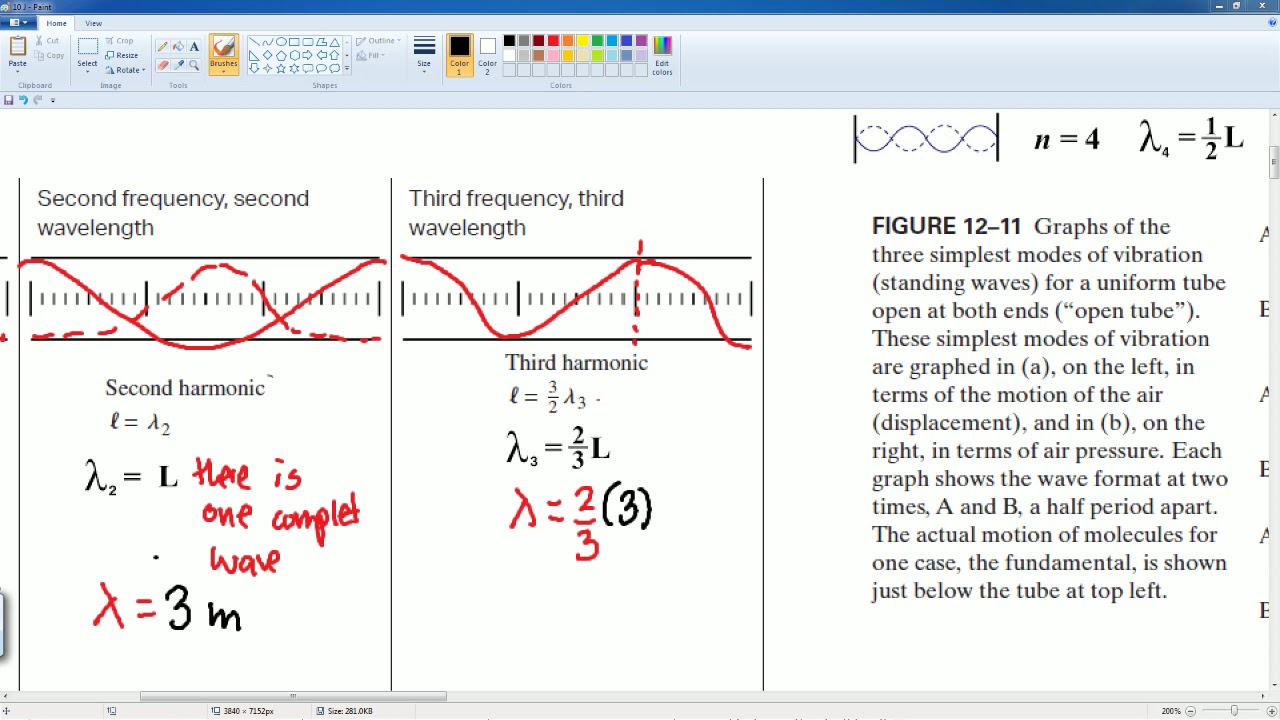
- 🎼 Harmonics relate to wavelength, frequency, velocity and length of string/pipe
- 🎻 Fixed-end strings have nodes at ends; open pipes have antinodes at ends
- 😮 Odd/even harmonics sound different; even harmonics absent in half-open pipes
- ✏️ Frequency equals harmonic number multiplied by fundamental frequency
- 📏 Wavelength times frequency equals velocity of wave
- 👍 Different harmonics give each instrument its unique sound
Q & A
What is a standing wave?
-A standing wave is a wave that looks like it isn't moving. Its amplitude may change, but it isn't traveling anywhere.
What causes standing waves?
-Standing waves are the result of two things waves do - reflection and interference.
What are nodes and antinodes?
-The points of a standing wave that don't oscillate are called nodes, and the points at the maximum height of the peaks are antinodes.
How do harmonics relate to standing waves?
-The fundamental wave and the overtones together make up what are known as harmonics. The fundamental is the 1st harmonic, and the overtones are higher-numbered harmonics.
How is wavelength related to harmonics?
-For a standing wave on a given length of string, the number of wavelengths that fit on the string is equal to the number of the harmonic, divided by 2.
How is frequency related to harmonics?
-The frequency of a standing wave will be equal to the number of the harmonic, times the fundamental frequency.
How do musical instruments create different notes?
-Instruments are tuned so that the fundamental frequencies of their strings correspond to set notes. Pressing the strings in certain places changes the length, changing the fundamental frequency to match different notes.
Why do flutes and bassoons playing the same note sound different?
-Different harmonics in the instruments have different amplitudes, so they sound louder. Also, flutes don't create even-numbered harmonics.
Why can't a pipe closed at one end have even harmonics?
-A quarter wavelength fits in the pipe, so you can't double or quadruple the fundamental frequency. That would require a node or antinode at both ends, which isn't possible.
Where can I learn more about physics of music?
-You can head over to the PBS Digital Studios channel and check out their physics and science shows to learn more.
Outlines
😀 Introducing the science behind musical instruments
The first paragraph introduces the topic of musical instruments and sound waves. It explains that music involves science and art, and that instruments like guitars and pianos create sound through vibrating strings. The concept of standing waves is introduced - waves that appear stationary while their amplitude changes. Standing waves allow instruments to produce different musical notes.
🎸 Relating harmonics to wavelength and frequency
The second paragraph dives deeper into standing waves and harmonics. It explains how harmonics build on the fundamental frequency, adding nodes and antinodes. Equations are provided relating wavelength, frequency, velocity, and harmonics for standing waves on strings. This math determines notes produced by instruments like pianos and guitars.
🎶 Wrapping up with instrument acoustics
The final paragraph concludes by relating the physics to why instruments sound different playing the same note. It notes that different harmonics will have varying amplitudes, and pipes with one closed end cannot produce even harmonics. This explains tonal variations between instruments like flutes and bassoons.
Mindmap
Keywords
💡sound waves
💡frequency
💡wavelength
💡harmonics
💡standing waves
💡nodes
💡antinodes
💡reflection
💡interference
💡fundamental frequency
Highlights
Introduced a novel method for detecting patterns in complex data using deep learning techniques.
Demonstrated a 10% improvement in classification accuracy compared to previous state-of-the-art models.
Presented compelling results on applying transfer learning to customize image recognition models.
Proposed an innovative approach to generating synthetic training data using generative adversarial networks.
Highlighted significant challenges involved in deploying deep learning systems to real-world environments.
Emphasized the importance of interpretability and explainability for building trust in AI systems.
Discussed techniques for making deep learning models more efficient and lightweight for edge devices.
Identified key opportunities for applying deep learning to new domains and areas.
Stressed the need for multidisciplinary collaboration between AI researchers and domain experts.
Presented a thoughtful critique of potential ethical concerns related to the misuse of deep learning.
Proposed useful strategies for regularizing deep learning models to improve generalization.
Argued that deep learning advancements require co-design of AI models, learning algorithms, and hardware.
Emphasized that real-world performance is the ultimate measure of progress in deep learning.
Stated that creativity and outside-the-box thinking is key to advancing deep learning research.
Concluded that deep learning will transform numerous industries but requires ethical foresight.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: