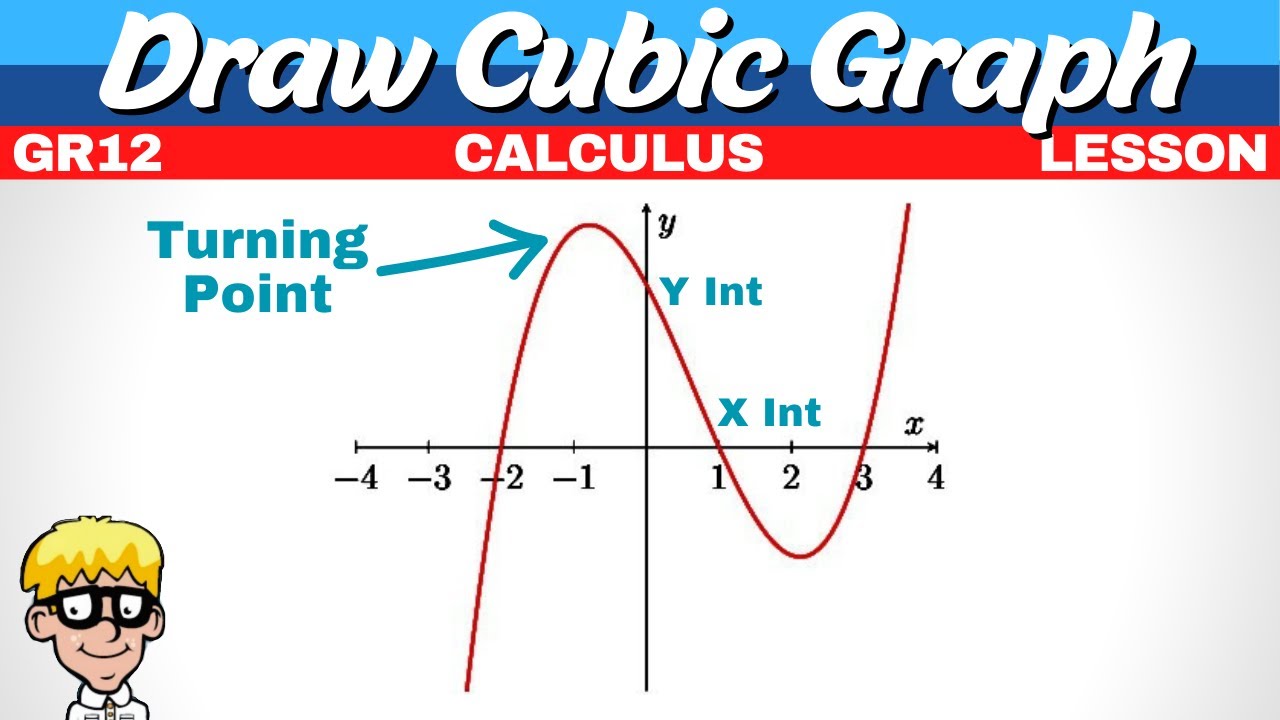
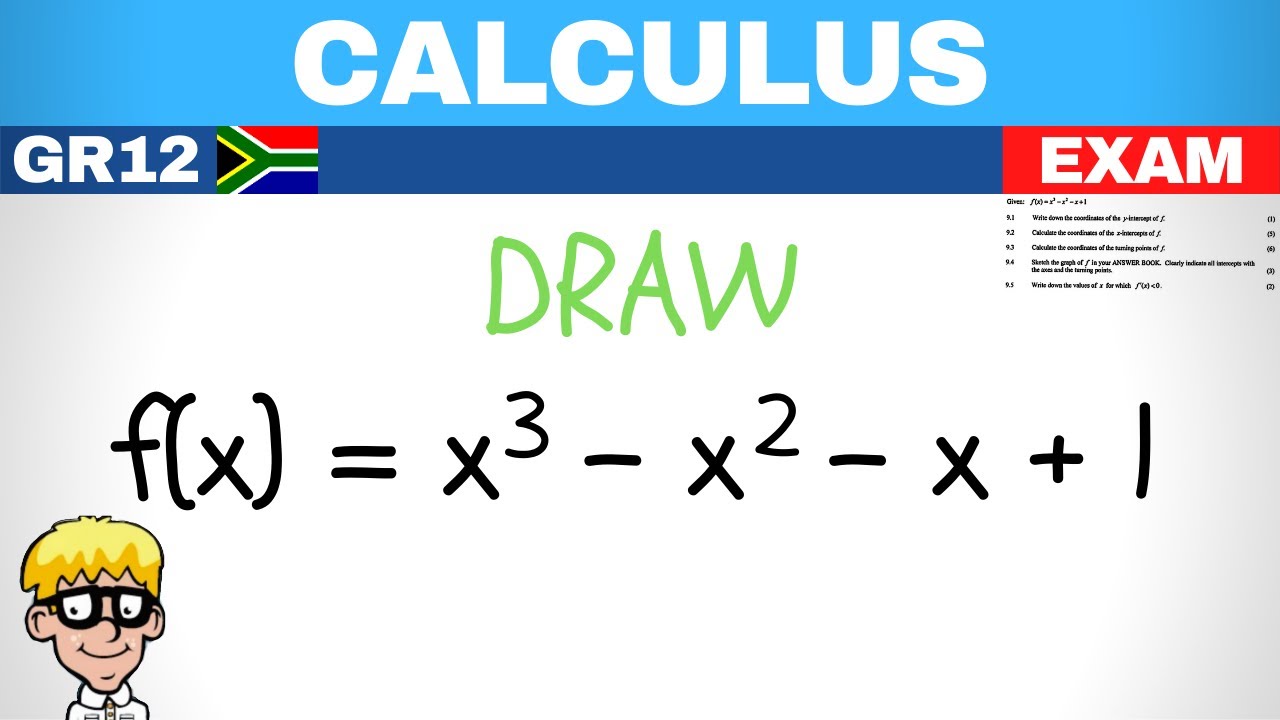Parabola Equation Grade 11 | Grade 11 Functions

Kevinmathscience
27 Sept 202012:05
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script teaches viewers two methods to find the equation of a parabola given its graph: the turning point method and the x-intercept method. The turning point method involves identifying the vertex and using an additional point to determine the equation. The x-intercept method uses the roots of the parabola and an extra point to derive the equation. The script provides step-by-step examples for each method, illustrating how to transform the derived equations into the standard form y = ax^2 + bx + c. It emphasizes that the standard form cannot be used to initially determine the graph or equation, but it can be achieved from the turning point or x-intercept forms.

Takeaways
  • 📚 There are two primary methods to find the equation of a parabola from its graph: the turning point method and the x-intercept method.
  • 📐 The turning point method requires knowledge of the parabola's turning point and at least one additional point.
  • 📈 The general form of a parabola's equation is \( y = a(x - h)^2 + k \), where \( a \) determines the direction and width, and \( (h, k) \) represents the vertex's coordinates.
  • 🔄 The 'p' and 'q' in the equation signify horizontal and vertical shifts of the parabola, respectively.
  • 📍 To find 'a' using the turning point method, substitute any point other than the turning point into the equation.
  • 🎯 The x-intercept method is used when the x-intercepts of the parabola are given, and it involves rewriting the equation in the form \( y = a(x - x_1)(x - x_2) \).
  • 🔢 The x-intercepts can be found by setting \( y = 0 \) in the equation and solving for \( x \).
  • 🔄 When given the x-intercepts, the equation can be simplified by substituting the intercepts into the equation and solving for 'a'.
  • 📉 To convert the derived equation into the standard form \( y = ax^2 + bx + c \), multiply out the brackets and simplify.
  • ✍️ The choice between the turning point method and the x-intercept method depends on the information provided in the problem.
  • 📝 The script provides step-by-step examples demonstrating how to apply both methods to derive the equation of a parabola from its graph.
Q & A

  • What are the two methods discussed in the video for finding the equation of a parabola when given its graph?

    -The two methods discussed are the turning point method and the x-intercept method.

  • What does the 'a' value in the parabola equation represent?

    -The 'a' value represents whether the graph is 'happy' or 'sad' and also indicates how wide or narrow the graph is.

  • What does the 'p' value in the parabola equation signify?

    -The 'p' value tells us whether the graph has been shifted to the left or to the right.

  • What does the 'q' value in the parabola equation signify?

    -The 'q' value tells us whether the graph has been shifted up or down.

  • How do you determine the shifts of a parabola in the turning point method?

    -To determine the shifts, you compare the original parabola's turning point at (0,0) with the given turning point of the graph and note the horizontal and vertical shifts.

  • What is the general form of a parabola's equation when using the turning point method?

    -The general form is y = a(x - h)² + k, where (h, k) is the turning point of the parabola.

  • What is the standard form of a parabola's equation when using the x-intercept method?

    -The standard form is y = a(x - x1)(x - x2), where x1 and x2 are the x-intercepts of the parabola.

  • How do you find the 'a' value in the turning point method?

    -You substitute any other point on the graph besides the turning point into the equation and solve for 'a'.

  • How do you find the 'a' value in the x-intercept method?

    -You substitute an additional point on the graph into the equation and solve for 'a'.

  • What is the final form of the parabola's equation that many questions will ask for?

    -Many questions will ask for the equation in the form y = ax² + bx + c.

  • How do you convert the parabola's equation from the turning point or x-intercept form to the form y = ax² + bx + c?

    -You multiply out the brackets in the equation and simplify to obtain the equation in the form y = ax² + bx + c.

  • Why is it not possible to directly use the y = ax² + bx + c form to get the graph or equation?

    -It is not possible because the y = ax² + bx + c form does not provide information about the shifts or the width of the parabola, which are needed to construct the graph or find the equation.

Outlines
00:00
📚 Introduction to Finding a Parabola's Equation

This paragraph introduces two methods for finding the equation of a parabola given its graph: the turning point method and the x-intercept method. The turning point method is used when the vertex of the parabola is known, along with at least one other point. The general form of a parabola's equation is discussed, where 'a' determines the width and direction of the parabola, and 'p' and 'q' indicate horizontal and vertical shifts, respectively. An example is given to demonstrate how to use the turning point and shifts to derive the equation, emphasizing that the original parabola's vertex is at (0,0) and any shifts are reflected in the equation.

05:01
🔍 Detailed Explanation of the Turning Point and X-Intercept Methods

The second paragraph delves deeper into the two methods for finding a parabola's equation. It explains how to use the turning point form and the x-intercept form to derive the standard quadratic form (y = ax^2 + bx + c). The importance of choosing the appropriate method based on the information provided (either the turning point or x-intercepts) is highlighted. The paragraph provides step-by-step instructions on substituting given points into the respective forms to solve for 'a', and then transforming the equation into the standard form. Examples are given to illustrate the process, emphasizing the need to multiply out brackets and simplify to reach the final equation.

10:01
📘 Applying the Methods to Examples

The final paragraph presents several examples to apply the turning point and x-intercept methods in practice. Each example demonstrates the process of identifying the appropriate method based on the given information, substituting points into the equation, solving for the unknown 'a', and then manipulating the equation to match the required standard form (y = ax^2 + bx + c). The examples include parabolas with given x-intercepts, turning points, and additional points to find 'a'. The paragraph concludes with a summary of the steps and the final equation for each example, reinforcing the methodology for solving such problems.

Mindmap
Keywords
💡Parabola
A parabola is a conic section, the intersection of a right circular cone with a plane parallel to the side of the cone. In the context of the video, it represents a U-shaped curve that is often used to model various phenomena in mathematics. The script discusses how to derive the equation of a parabola from its graph, which is central to understanding the mathematical concepts presented.
💡Equation
In mathematics, an equation is a statement that asserts the equality of two expressions, which can include variables, constants, and operators. The video script focuses on finding the equation of a parabola when given its graph, which is essential for analyzing and applying the parabola in various mathematical problems.
💡Turning Point Method
The turning point method is a technique used to find the equation of a parabola when the vertex, or turning point, of the parabola is known. The video explains that this method requires an additional point besides the turning point to determine the specific equation, illustrating its use with an example where the turning point is at (3, -2).
💡X-intercept Method
The x-intercept method is another approach to finding the equation of a parabola, which involves using the points where the parabola crosses the x-axis, known as x-intercepts. The script describes how to use this method by rewriting the equation in a factored form using the x-intercepts and an additional point to solve for the unknown variable 'a'.
💡Vertex
The vertex of a parabola is the point where the parabola turns, either at its maximum or minimum point. In the video, the vertex is used to determine the shifts in the parabola's position, with the script mentioning that the original parabola starts at (0, 0) and then being shifted to a new location, such as (3, -2).
💡Shift
A shift in the context of the video refers to the horizontal and vertical movement of the parabola from its original position. The script explains how to determine these shifts by comparing the original vertex (0, 0) to the vertex of the given parabola, which helps in writing the correct equation.
💡Coefficient 'a'
The coefficient 'a' in the equation of a parabola determines the width or steepness of the parabola. The video script demonstrates how to find the value of 'a' by substituting known points into the equation and solving for it, which is crucial for writing the complete equation of the parabola.
💡Standard Form
The standard form of a parabolic equation is typically written as y = ax^2 + bx + c. The video script discusses how to transform the equation obtained from either the turning point method or the x-intercept method into this standard form by expanding and simplifying the expressions.
💡Factored Form
The factored form of a parabolic equation is an alternative way to express the equation, especially when the x-intercepts are known. The script uses the factored form y = a(x - x1)(x - x2) to demonstrate how to incorporate the x-intercepts into the equation and solve for the coefficient 'a'.
💡Solving for 'a'
Solving for 'a' is a process described in the video where an additional point on the parabola is used to determine the value of the coefficient 'a'. This is done by substituting the x and y values of the point into the equation derived from either the turning point or x-intercept method and solving the resulting equation.
Highlights

Introduction to two methods for finding the equation of a parabola from its graph: the turning point method and the x-intercept method.

Explanation of the general form of a parabola equation and the significance of 'a', 'p', and 'q' in determining the shape and position.

How to determine the shifts of a parabola using the turning point method and the importance of the original parabola's coordinates.

Demonstration of finding 'a' by substituting any other point on the graph besides the turning point.

Conversion from the derived parabola equation to the standard form y = ax^2 + bx + c.

Introduction to the x-intercept method and its requirements, including two x-intercepts and an extra point.

The standard form for equations using the x-intercept method and the role of 'a' in determining the graph's width.

Process of substituting known x-intercepts into the equation and solving for 'a'.

Explanation of why it's not possible to derive the graph or equation using y = ax^2 + bx + c without the turning point or x-intercept form.

Guidance on choosing the appropriate method based on the information provided: turning point or x-intercepts.

Example problem demonstrating the use of the x-intercept layout with given x-intercepts.

Step-by-step process of solving for 'a' using a given point on the graph and substituting it into the equation.

Conversion of the derived equation into the standard form required by the problem statement.

Example of using the turning point form for a parabola with a given turning point and shifts.

Finding 'a' by substituting another point on the graph and solving the derived equation.

Final steps of multiplying out brackets and simplifying to achieve the equation in the required form.

Conclusion emphasizing the importance of using the appropriate method based on the given information to find the parabola's equation.

Transcripts

Browse More Related Video

How To Find The Vertex of a Parabola - Standard Form, Factored & Vertex Form

Calculus Grade 12 Exam Questions

Draw Cubic Graph Grade 12

How To Find The Equation of a Secant Line

Equation of a tangent line [IB Maths AI SL/HL]

Calculus grade 12: Exam

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Parabola EquationsTurning PointX-Intercept MethodGraph AnalysisMathematics TutorialEquation DerivationAlgebraic GeometryEducational ContentMath Problem SolvingGraphing Techniques