Scales of Measurement - Nominal, Ordinal, Interval, Ratio (Part 1) - Introductory Statistics

Quantitative Specialists
1 Jul 201505:51
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video introduces the concept of scales of measurement, defining measurement as the process of assigning numbers to objects following a set of rules. It explores four key scales: nominal, where numbers differentiate without implying order; ordinal, which adds a meaningful sequence to the differentiation; interval, which builds on ordinal by including equal intervals between values, exemplified by temperature measurements; and ratio, which is mentioned but not detailed in the provided transcript. The video uses relatable examples like gender assignment and sports rankings to clarify each scale, making the content accessible and engaging.

Takeaways
  • 📏 Measurement is the process of assigning numbers to objects according to a set of rules.
  • 🔢 The four scales of measurement are nominal, ordinal, interval, and ratio, each with distinct characteristics.
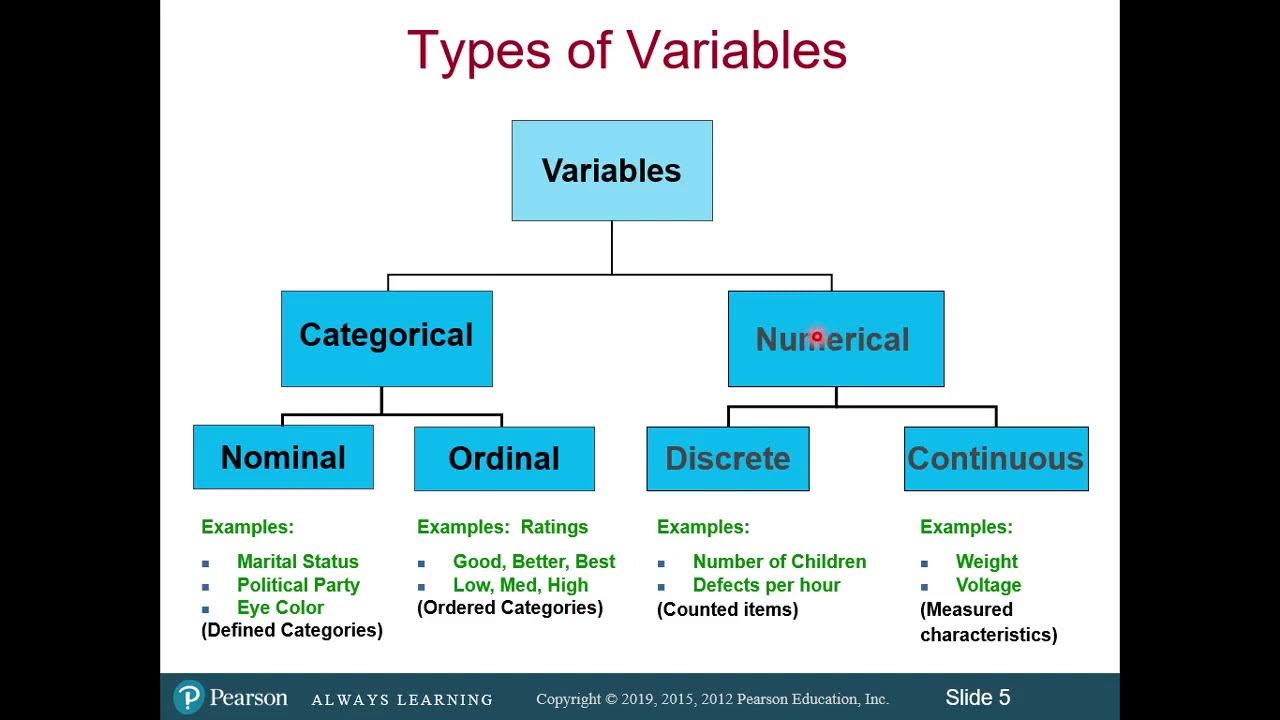
  • 🏷️ Nominal scale assigns numbers to differentiate objects without any inherent meaning, like gender (1 for males, 2 for females).
  • 👕 Baseball uniform numbers are an example of nominal scale, where numbers only differentiate players without indicating any performance or position.
  • 🥇 Ordinal scale not only differentiates but also ranks objects in a meaningful order, such as race finishing positions.
  • 🏆 Ordinal data allows us to know the relative performance of objects, like who finished first, second, or third in a competition.
  • 🌡️ Interval scale builds on ordinal by adding equal intervals between categories, as seen with Fahrenheit temperature measurements.
  • 🌡️ A one-degree difference on an interval scale, like between 78°F and 79°F, has the same meaning throughout the scale.
  • 🔄 Interval scale implies that the difference between any two points is consistent, unlike ordinal which only indicates order.
  • 🔄 The script does not provide a complete explanation for the ratio scale, but it is implied to have all the properties of interval plus a true zero point, allowing for the comparison of ratios.
  • 📚 Examples are crucial for differentiating between the scales of measurement, as they illustrate the practical application of each.
Q & A

  • What is the definition of measurement according to the video?

    -Measurement can be defined as the process of applying numbers to objects according to a set of rules.

  • Can you provide an example of how measurement is applied in everyday life?

    -An everyday example of measurement is measuring someone's height by having them stand against a wall and using a tape measure to determine their height in feet and inches.

  • How many scales of measurement are typically discussed in introductory statistics textbooks?

    -There are four scales of measurement discussed: nominal, ordinal, interval, and ratio.

  • What is the primary purpose of numbers on a nominal scale?

    -On a nominal scale, numbers are used to differentiate between objects, with no inherent meaning to the numbers themselves.

  • What is an example of a nominal scale measurement given in the video?

    -An example of a nominal scale measurement is assigning numbers to represent gender, where males get a 1 and females get a 2.

  • How do baseball uniform numbers serve as an example of nominal measurement?

    -Baseball uniform numbers are an example of nominal measurement because they differentiate between players without indicating any performance or positional information.

  • What is the key difference between nominal and ordinal scales of measurement?

    -While both nominal and ordinal scales use numbers to categorize objects, ordinal scales also have a meaningful order, allowing for ranking.

  • Can you explain the concept of an ordinal scale with an example?

    -An ordinal scale assigns numbers to objects in a way that indicates order or ranking. An example is the placement of runners in a race, where first, second, and third indicate their relative performance.

  • What is the main characteristic of interval measurement that distinguishes it from ordinal measurement?

    -Interval measurement, like ordinal, has order, but it also includes equal intervals between adjacent categories, meaning the difference between any two numbers is consistent.

  • How does the Fahrenheit temperature scale exemplify interval measurement?

    -The Fahrenheit temperature scale exemplifies interval measurement because the difference between any two degrees is the same, regardless of where they are on the scale (e.g., the difference between 78°F and 79°F is the same as between 45°F and 46°F).

  • What is the final scale of measurement mentioned in the video, and what are its characteristics?

    -The final scale mentioned in the video is the ratio scale, which is not fully explained in the transcript but typically includes all the characteristics of interval scales and also allows for meaningful ratios, including a true zero point.

Outlines
00:00
📏 Introduction to Scales of Measurement

This paragraph introduces the concept of measurement as the process of assigning numbers to objects according to a set of rules, using the example of measuring a person's height. It then outlines the four scales of measurement: nominal, ordinal, interval, and ratio, which are the focus of the video. The scales are introduced with the promise of examples to follow, which will help differentiate between them.

05:04
🏷 Understanding Nominal Scales

The first scale discussed is the nominal scale, where numbers are assigned to objects to differentiate between them without any inherent meaning. Examples given include gender assignment where males are assigned a '1' and females a '2', and baseball uniform numbers that distinguish players but do not convey any performance-related information. The key takeaway is that nominal numbers are used for identification and categorization purposes only.

🥇 Exploring Ordinal Scales

Ordinal scales are introduced as a step up from nominal, where numbers not only differentiate but also indicate a meaningful order. The examples provided include race finishing positions and election results, where the assigned numbers like '1st', '2nd', '3rd' reflect the order of finish or outcome. The summary emphasizes that ordinal data allows for ranking but does not provide information about the 'distance' between the ranks.

℉ Delving into Interval Scales

Interval scales are characterized by having both order and equal intervals between adjacent categories, unlike ordinal scales. The example of temperature measurement in Fahrenheit is used to illustrate this point, where the difference between 78°F and 79°F is the same as between 45°F and 46°F. The summary highlights that interval scales provide a consistent unit of measurement across the scale, allowing for meaningful comparisons of differences.

Mindmap
Keywords
💡Measurement
Measurement is the process of assigning numbers to objects or events according to a set of rules. In the context of the video, measurement is fundamental to understanding the scales of measurement, which are different ways of assigning numbers to data. The video script uses the example of measuring a person's height to illustrate how numbers are applied to an object (a person) following a specific rule (extending the tape measure from the ground to the top of the head).
💡Scales of Measurement
Scales of measurement refer to the different levels at which data can be measured and quantified. The video script introduces four main scales: nominal, ordinal, interval, and ratio. These scales are crucial for understanding how data is organized and interpreted in statistics. Each scale has unique characteristics that determine what kind of mathematical operations can be performed on the data.
💡Nominal
Nominal is the first scale of measurement discussed in the video. It involves assigning numbers to objects where the numbers are used only to differentiate between them and have no intrinsic meaning. The video provides the example of gender, where males are assigned the number 1 and females the number 2, to illustrate that the numbers serve only to distinguish between categories without implying any order or magnitude.
💡Ordinal
Ordinal is a scale of measurement where numbers are assigned to objects in a way that indicates a meaningful order or ranking. The video script explains that ordinal data allows us to rank items, such as the positions in a race (first, second, third), where the numbers signify the order in which participants finished, thus providing information about their relative performance.
💡Interval
Interval is a scale of measurement that builds upon the ordinal scale by adding the requirement that the intervals between the numbers are equal. The video uses the example of temperature measured in degrees Fahrenheit to illustrate this concept. The difference between 78 and 79 degrees Fahrenheit is the same as the difference between 45 and 46 degrees, showing that each unit of measurement is consistent across the scale.
💡Ratio
Ratio is the final scale of measurement mentioned in the video script, but it is not fully explained due to the transcript being cut off. However, based on standard definitions, the ratio scale is similar to the interval scale in that it has equal intervals between values, but it also has a true zero point, which means it can represent the absence of a quantity and allow for meaningful ratios to be calculated.
💡Differentiation
Differentiation in the context of the video refers to the process of distinguishing between different objects or categories using numbers. This concept is particularly relevant to the nominal scale of measurement, where numbers are assigned to differentiate objects without implying any order or magnitude. For example, assigning the number 1 to males and 2 to females differentiates the two groups without suggesting any inherent ranking or value.
💡Order
Order is a concept that is central to the ordinal scale of measurement. It refers to the arrangement of objects in a sequence that reflects their relative position or value. The video script uses the example of race positions (first, second, third) to demonstrate how numbers can indicate the order in which participants completed the race, thus providing information about their performance relative to each other.
💡Equal Intervals
Equal intervals are a defining characteristic of the interval scale of measurement. They refer to the consistent difference between each unit of measurement along the scale. The video script explains this concept using the Fahrenheit temperature scale, where the difference between 78 and 79 degrees is the same as between any other pair of adjacent degrees, indicating that the intervals are equal throughout the scale.
💡Examples
Examples are used throughout the video script to illustrate the different scales of measurement. They serve to clarify abstract concepts by providing concrete instances that viewers can relate to. For instance, the script uses the example of gender to explain the nominal scale, race positions for ordinal, and temperature in Fahrenheit for interval, making the theoretical concepts more tangible and easier to understand.
💡Statistical Analyses
Statistical analyses are mentioned in the video script as a context where the scales of measurement are applied. This term refers to the process of examining and interpreting data using statistical methods. The video emphasizes the importance of understanding the scales of measurement in conducting statistical analyses, as they determine the type of data that can be analyzed and the kinds of conclusions that can be drawn.
Highlights

Measurement is defined as the process of applying numbers to objects according to a set of rules.

An example of measurement is measuring someone's height using a tape measure and a ruler.

There are four scales of measurement: nominal, ordinal, interval, and ratio.

Nominal scale assigns numbers to objects where the numbers indicate different objects without any inherent meaning.

Gender is an example of nominal measurement, where males are assigned a 1 and females a 2.

Baseball uniform numbers are another example of nominal measurement, differentiating players without indicating any performance metrics.

Ordinal scale assigns numbers that have a meaningful order, such as the placement in a race.

Ordinal data allows us to rank objects, unlike nominal which only differentiates.

Interval scale builds on ordinal by having equal intervals between adjacent categories.

Temperature measured in degrees Fahrenheit is an example of interval measurement, where one degree difference is consistent across the scale.

The difference between 78 and 79 degrees Fahrenheit is the same as between 45 and 46 degrees.

Interval scale is contrasted with ordinal, where differences between categories are not necessarily equal.

Ratio scale is mentioned as the final scale of measurement, but not detailed in the provided transcript.

Examples are crucial for differentiating between the four scales of measurement.

The video aims to clarify the concept of measurement and its scales through easy-to-understand examples.

The rules of measurement dictate how numbers are applied to objects, as illustrated in the height measurement example.

The video breaks down complex statistical concepts into simple, relatable scenarios for better understanding.

Transcripts

Browse More Related Video

Scales of Measurement - Nominal, Ordinal, Interval, Ratio (Part 2) - Introductory Statistics

Classification of Variables and Types of Measurement Scales

Data Types - Levels of Data Measurements - Nominal Ordinal Interval Ratio | Statistics | Research

Scales of Measurement - Nominal, Ordinal, Interval, & Ratio Scale Data

Introduction to Levels of Measurement: Nominal, Ordinal, Interval, Ratio

Nominal, Ordinal, Interval & Ratio Data: Simple Explanation With Examples

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Measurement ScalesEducational VideoScales of MeasurementStatistical AnalysisData TypesNominal ScaleOrdinal ScaleInterval ScaleRatio ScaleHeight MeasurementRace Results