Physics - Diffraction of Light (4 of 4) Circular Diffraction Patterns

Michel van Biezen
14 May 201304:18
EducationalLearning
32 Likes 10 Comments

TLDRThis script explores the concept of angular resolution in optical instruments, including the human eye. It explains the diffraction pattern produced by a circular aperture and the formula to calculate the angle of resolution, which is vital for distinguishing closely spaced objects. The script demonstrates the calculation using typical values for human vision and compares it with the superior vision of an eagle and the exceptional resolution of the Hubble Space Telescope, highlighting the impact of aperture size and wavelength on resolution capabilities.

Takeaways
  • 🌟 Optical instruments like the human eye, cameras, and telescopes use circular apertures to focus light.
  • 🔍 The angle of resolution is the angle between the central maximum and the first dark fringe in a diffraction pattern.
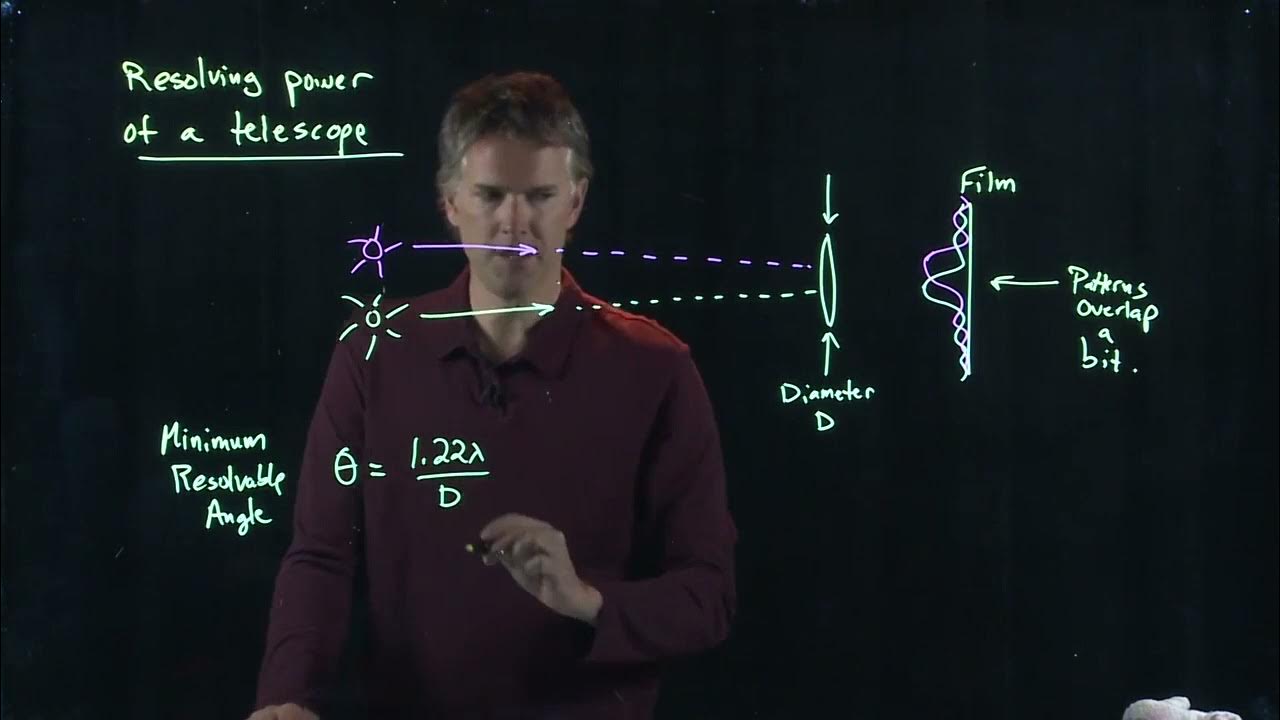
  • 📐 The formula for angular resolution is given by the sine of theta equals 1.22 times lambda over D, where D is the diameter of the aperture and lambda is the wavelength of light.
  • 🌈 The angle of resolution depends on the wavelength of light and the diameter of the aperture.
  • 👀 Smaller angular resolution indicates sharper image quality and the ability to resolve closely-spaced objects.
  • 📏 For small angles, the sine of theta is approximately equal to theta, simplifying the calculation of angular resolution.
  • 🔬 A larger aperture (D) or smaller wavelength (lambda) results in a smaller angle of resolution, improving resolution quality.
  • 🌍 The human eye has a typical pupil size of about 4 millimeters and a wavelength of visible light at 500 nanometers, leading to a high-resolution capability.
  • 🦅 Eagles have a larger pupil diameter, around 1.5 centimeters, which results in even better resolution than human vision.
  • 🚀 The Hubble Space Telescope, with a mirror diameter of 2.4 to 2.8 meters, has an exceptionally small angle of resolution, allowing for extremely precise imaging of distant objects.
  • 📝 Understanding the relationship between aperture size, wavelength, and angular resolution is crucial for designing high-resolution optical instruments.
Q & A

  • What is the diffraction pattern of a circular aperture?

    -The diffraction pattern of a circular aperture consists of a series of bright and dark rings, with the dark fringes being circular due to the circular shape of the opening.

  • Why are most optical instruments, including the human eye, designed with circular openings?

    -Most optical instruments, including the human eye, are designed with circular openings because the natural shape of the eye, camera lenses, and telescope mirrors is circular, which facilitates light to pass through a round aperture.

  • What is the angle of resolution in the context of optical instruments?

    -The angle of resolution refers to the angle between the central maximum and the first dark fringe in the diffraction pattern of a circular aperture, which is a measure of the ability to distinguish between closely spaced objects.

  • What is the formula used to calculate the angle of resolution for a circular aperture?

    -The formula to calculate the angle of resolution is given by the sine of theta equals 1.22 times the wavelength (lambda) over the diameter (D) of the circular opening.

  • How does the wavelength of light affect the angle of resolution?

    -The angle of resolution depends on the wavelength of light; a smaller wavelength results in a smaller angle of resolution, which means better resolution and the ability to see finer details.

  • What is the typical wavelength of visible light used in the example?

    -The example uses a typical wavelength for visible light, which is 500 nanometers.

  • What is the typical size of the human pupil, and how does it relate to the angle of resolution?

    -The typical size of the human pupil is about 4 millimeters. Using this diameter in the formula, the example calculates the typical resolution angle for human vision.

  • How does the diameter of the pupil in an eagle compare to that of a human, and what is the implication for vision?

    -An eagle's pupil diameter is larger, approximately 1.5 centimeters, which results in a smaller angle of resolution and thus better vision compared to humans.

  • What is the significance of the Hubble Space Telescope's large aperture in terms of angular resolution?

    -The Hubble Space Telescope has a large aperture of about 2.4 to 2.8 meters, which provides an extremely small angle of resolution, allowing it to see distant objects with high accuracy and clarity.

  • What does the calculated angle of resolution for human vision indicate about our visual capabilities?

    -The calculated angle of resolution for human vision, which is 8.73 times 10 to the minus 3 degrees, indicates that human vision has extremely acute capabilities, allowing us to resolve small, closely-spaced objects.

Outlines
00:00
🔍 Diffraction Pattern and Angular Resolution in Optical Instruments

This paragraph discusses the diffraction pattern produced by a circular aperture, which is common in optical instruments such as the human eye, cameras, and telescopes. The main focus is on determining the angle of resolution, which is the angle between the central maximum and the first dark fringe in the diffraction pattern. The formula for calculating this angle involves the sine of theta being equal to 1.22 times the wavelength of light (lambda) divided by the diameter of the aperture (D). The paragraph explains that a smaller angle indicates better resolution, allowing for the distinction of closely-spaced objects. It also notes that the angle of resolution is dependent on both the wavelength of light and the diameter of the aperture, with a larger aperture or shorter wavelength leading to a sharper image.

Mindmap
Keywords
💡Diffraction Pattern
A diffraction pattern is the distribution of light or other waves as they bend around obstacles and spread out after passing through an aperture or a slit. In the context of the video, the diffraction pattern of a circular aperture is discussed, which is relevant to understanding the resolution of optical instruments. The script explains how the pattern appears when light passes through a circular opening, such as in the human eye or a camera lens.
💡Aperture
In optics, the aperture refers to the opening in a lens through which light travels. It plays a crucial role in the amount of light that enters a camera or the human eye. The script mentions that most optical instruments, including the human eye, have circular apertures which contribute to the formation of diffraction patterns and affect the resolution of the images formed.
💡Resolution
Resolution in optics is the ability to distinguish between closely spaced objects. The script discusses the angle of resolution, which is the angle between the central maximum and the first dark fringe in a diffraction pattern. A smaller angle of resolution indicates better optical performance, allowing for the differentiation of finer details in the observed scene.
💡Central Maximum
The central maximum is the brightest point in a diffraction pattern, located at the center. The script refers to the central maximum when explaining how to measure the angle of resolution, which is essential for determining the resolving power of an optical system.
💡First Dark Fringe
The first dark fringe in a diffraction pattern is the first complete dark area that occurs away from the central maximum. The script uses the first dark fringe as a reference point to calculate the angle of resolution, which is a measure of the optical system's ability to distinguish between two points.
💡Sine of Theta
Theta, in the context of the script, represents the angle of resolution. The sine of theta is used in the formula to calculate the angle of resolution, where it is set equal to 1.22 times the ratio of the wavelength of light to the diameter of the aperture. This mathematical relationship is central to determining the resolving capability of an optical instrument.
💡Wavelength
The wavelength is the distance between two consecutive points in a wave that are in the same phase. In the script, the wavelength of light (lambda) is a key factor in the equation for calculating the angle of resolution. Different wavelengths affect the diffraction pattern and thus the resolution of an optical system.
💡Diameter
The diameter of the circular opening in an optical instrument, denoted as 'D' in the script, is a critical parameter in determining the angle of resolution. A larger diameter allows for a smaller angle of resolution, which improves the ability to resolve fine details.
💡Human Eye
The human eye is used as an example in the script to illustrate the concept of optical resolution. The size of the pupil, which acts as the aperture, is compared to other optical instruments to demonstrate how it affects the resolution of the images we see.
💡Eagle Vision
The script contrasts human vision with that of an eagle, noting that an eagle's larger pupil diameter allows for a smaller angle of resolution and thus superior visual acuity. This comparison highlights the impact of aperture size on the resolving power of different optical systems.
💡Hubble Space Telescope
The Hubble Space Telescope is mentioned in the script as an example of an optical instrument with a very large aperture, which results in an exceptionally small angle of resolution. This allows the telescope to observe distant objects with high precision, demonstrating the principle of angular resolution on a large scale.
Highlights

Introduction to the diffraction pattern of a circular aperture and its relevance to optical instruments.

Explanation of how the human eye, like other optical instruments, uses a circular opening to focus light.

The concept of the angle of resolution and its importance in distinguishing closely-spaced objects.

The mathematical formula for calculating the angle of resolution using the diameter of the aperture and the wavelength of light.

The relationship between the wavelength of light and the diameter of the aperture on the angle of resolution.

The approximation that sine of theta is equal to theta for very small angles, simplifying the resolution calculation.

The impact of aperture size on the angular resolution, with larger apertures providing better resolution.

The calculation of the angular resolution for human vision using a typical pupil diameter and visible light wavelength.

The surprising result that human vision has an extremely acute angle of resolution, indicating high visual acuity.

Comparison of human vision with that of an eagle, which has a larger pupil diameter and superior visual acuity.

The significance of the Hubble Space Telescope's large mirror diameter in achieving a very fine angular resolution.

The practical application of understanding angular resolution in the design of optical instruments for improved imaging capabilities.

The importance of the angle of resolution in the field of optics and its role in the functionality of various instruments.

The detailed step-by-step calculation process for determining the angular resolution of the human eye.

The use of a calculator to perform the actual calculations for the angular resolution, demonstrating the practical aspect of the theory.

The comparison of the calculated angle of resolution with the capabilities of the human eye and other animals, emphasizing the differences.

Transcripts

Browse More Related Video

Optical Instruments: Crash Course Physics #41

Ultrasound Physics with Sononerds Unit 12b

Axial Resolution | Ultrasound Physics | Radiology Physics Course #17

Resolving Power of a Telescope | Physics with Professor Matt Anderson | M28-14

How Optics Work - the basics of cameras, lenses and telescopes

Lateral and Elevational Resolution | Ultrasound Physics | Radiology Physics Course #18

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Optical ResolutionHuman VisionEagle EyesHubble TelescopeAngular MeasurementLight WavelengthAperture SizeAcute VisionOptical PhysicsAstronomical InstrumentsVision Comparison