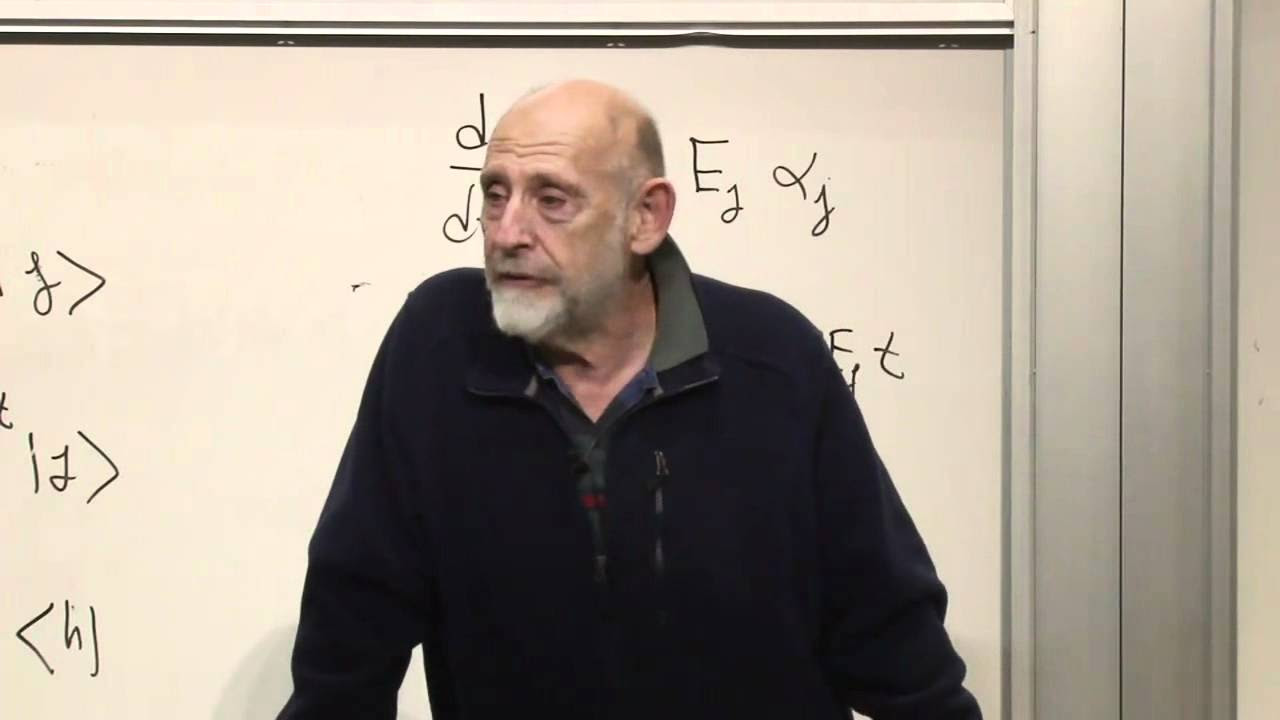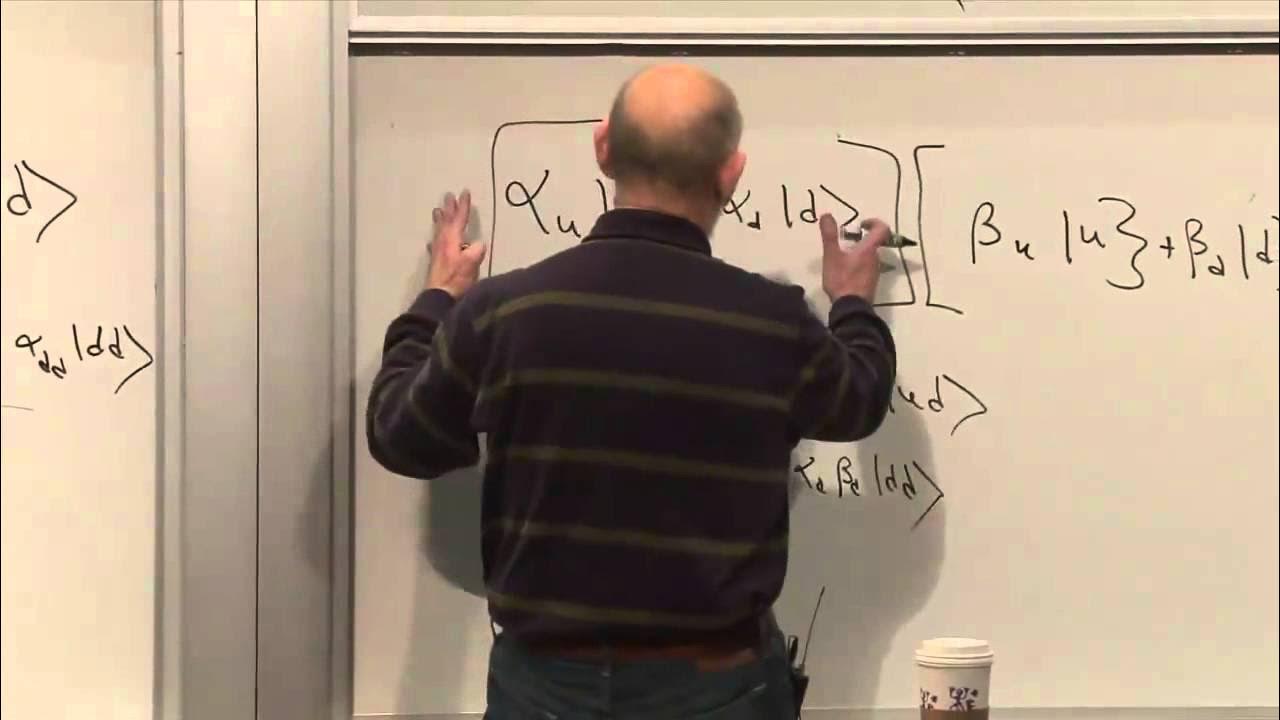4. Resonance IV
TLDRThe lecture delves into the dynamics of classical and quantum mechanical magnetic moments in magnetic fields, focusing on rapid adiabatic passage as a method for manipulating spin systems. It explores the adiabatic condition and its significance in maintaining alignment during magnetic field changes. The Landau-Zener parameter is introduced, connecting classical and quantum perspectives. The Hamiltonian for a two-level system is derived, and its implications for quantum coherence and the dressed atom picture are discussed, leading to an examination of the Landau-Zener problem and its relevance in quantum state transitions.
Takeaways
- 📚 The lecture discusses the behavior of classical and quantum mechanical magnetic moments in magnetic fields, focusing on rapid adiabatic passage as a method to manipulate these systems.
- 🌀 Professor explains that rapid adiabatic passage allows for the inversion of spin in a system by sweeping the frequency of an oscillating magnetic field through resonance, creating an effective magnetic field that rotates and the atom follows adiabatically.
- 🤔 The question of how slow the adiabatic process needs to be is addressed, deriving the adiabatic condition that the rotation of the effective magnetic field must be much slower than the Larmor precession frequency.
- 🔍 Through a counterexample, it's shown that if the magnetic field direction jumps, the atom loses alignment, emphasizing the need for a gradual change in the magnetic field direction for adiabaticity.
- 🔗 The connection between the classical picture and quantum mechanics is made, showing that the Heisenberg equation of motion for a quantum system with a magnetic moment in an applied field results in precession, an exact result for quantum mechanics.
- 🧲 The Hamiltonian for a two-level system, such as a spin-1/2 particle in a magnetic field, is introduced, highlighting its importance in understanding quantum systems and its application in various physics problems.
- 🌐 The concept of 'dressed states' is introduced, which are the eigenstates and eigenenergies of the Hamiltonian when a two-level system is interacting with a mode of the electromagnetic field.
- 🔄 The solution to the two-level system Hamiltonian involves a unitary transformation to a rotating frame, which simplifies the problem to a time-independent one and allows for the calculation of transition probabilities.
- 🚀 The Landau-Zener problem is discussed, which describes the quantum mechanical process of sweeping a system through an avoided crossing and the associated transition probabilities.
- ⚛️ The perturbative approach to estimate the small transition probability in the non-adiabatic regime is introduced, providing insight into processes like evaporative cooling in ultra-cold atomic gases.
- 🕒 The effective time during a Landau-Zener sweep is identified as the period during which the system adds substantial amplitude coherently to the second state, which is crucial for understanding the transition probability.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the discussion of classical and quantum mechanical magnetic moments when exposed to magnetic fields, with a focus on rapid adiabatic passage and its quantum mechanical aspects.
What is rapid adiabatic passage?
-Rapid adiabatic passage is a method to manipulate classical and quantum systems. It involves sweeping the resonance frequency of an oscillating magnetic field through the system's resonance, creating an effective magnetic field that causes the spin to invert if the change is done adiabatically.
What is the adiabatic condition in the context of this lecture?
-The adiabatic condition is that the rotation of the effective magnetic field must be much slower than the precession frequency of the spin. This ensures that the system remains in the same quantum state during the process.
What is the significance of the Larmor frequency in the adiabatic condition?
-The Larmor frequency, which is the precession frequency around the effective magnetic field, must be much larger than the rate of change of the angle of the effective magnetic field (theta dot) for the adiabatic condition to be met.
What is the Landau-Zener parameter and how is it related to the adiabatic condition?
-The Landau-Zener parameter is a result derived from the classical picture, which is later encountered in the quantum mechanical version of rapid adiabatic passage. It is used to determine the probability of a system transitioning between states during a sweep through an avoided crossing, and it is related to the adiabatic condition through the ratio of the Rabi frequency squared to the sweep rate.
What is the relevance of the Rabi frequency in the context of this lecture?
-The Rabi frequency is the frequency at which the population of a two-level system oscillates between the ground and excited states under the influence of a resonant driving field. It is used to describe the dynamics of the system and is a key factor in determining the adiabatic condition.
How does the Hamiltonian for a two-level system in a magnetic field differ from the classical description?
-The Hamiltonian for a two-level system in a magnetic field is an exact quantum mechanical description that includes the energy splitting of the system and the interaction with the magnetic field. While it leads to the same precession dynamics as the classical description, it allows for a deeper understanding of the system's quantum behavior, including phenomena like Rabi oscillations.
What is the significance of the rotating frame transformation in solving the Hamiltonian for a two-level system?
-The rotating frame transformation is a unitary transformation that simplifies the Hamiltonian to a time-independent form, making it easier to solve. It effectively rotates the frame of reference along with the system, eliminating the time-dependence and allowing for the calculation of stationary states.
What is the Landau-Zener problem and how does it relate to the concept of avoided crossing?
-The Landau-Zener problem is a quantum mechanical description of a system swept through an avoided crossing by changing an external parameter, such as the frequency of a driving field. It deals with the probability of the system transitioning between states during this sweep, and it is a fundamental concept in understanding non-adiabatic transitions.
How does the concept of 'dressed states' relate to the Hamiltonian of a two-level system?
-Dressed states are the eigenstates of the Hamiltonian for a two-level system when it is coupled to a quantized mode of the electromagnetic field. They represent the modified states of the system due to its interaction with the field, and they are used to describe phenomena such as the Jaynes-Cummings model or the Rabi model.
What is the difference between using perturbation theory for a coherent transition and an incoherent transition in the context of the Landau-Zener problem?
-In the context of the Landau-Zener problem, using perturbation theory for a coherent transition involves calculating the amplitude of the transition based on the coupling Hamiltonian and the effective time of interaction, resulting in a quadratic time dependence. For an incoherent transition, Fermi's golden rule is applied, giving a constant transition rate and a linear time dependence, which accounts for the loss of coherence due to factors like spontaneous emission or coupling to a reservoir.
What is the effective time in the Landau-Zener crossing, and why is it significant?
-The effective time in the Landau-Zener crossing is the duration during which the system is coherently driven and experiences a phase shift that contributes to the transition amplitude. It is significant because it determines the probability of the transition and is related to the Landau-Zener parameter, which describes the non-adiabatic transition probability.
Outlines
🧲 Introduction to Magnetic Moments in Classical and Quantum Systems
The script begins with a discussion on the impact of magnetic fields on classical and quantum mechanical magnetic moments, revisiting the concept of rapid adiabatic passage. It explains how a spin system can be manipulated by sweeping the frequency of an oscillating magnetic field through resonance, creating an effective magnetic field that causes the spin to invert. The focus then shifts to defining the adiabatic condition, which requires the rotation of the effective magnetic field to be significantly slower than the Larmor precession frequency, to ensure the system remains aligned with the magnetic field. A counterexample illustrates what happens if the magnetic field changes too abruptly. The segment ends with an introduction to the Landau-Zener parameter, a key concept in understanding quantum mechanical transitions that will be discussed later.
🔍 Deriving the Adiabatic Condition for Spin Systems
This paragraph delves into the derivation of the adiabatic condition for spin systems. It starts by discussing the precession of a spin around a magnetic field and the critical nature of the resonance moment when the effective magnetic field changes due to the addition of a fictitious field. The paragraph then describes the calculation of the angular velocity, theta dot, during the sweep rate of the frequency and its relation to the Rabi frequency. The adiabatic condition is expressed as a requirement for the sweep rate to be smaller than the square of the Rabi frequency. This leads to a general condition for adiabatic processes, emphasizing the importance of a slow change in frequency relative to the relevant frequency squared. The paragraph concludes by connecting this classical result to the Landau-Zener parameter, which will be encountered in quantum mechanical treatments of adiabatic passage.
🌀 Heisenberg's Equation of Motion for Quantum Spins
The script moves on to the application of Heisenberg's equation of motion to quantum spins in a magnetic field. It emphasizes that the principles learned for classical magnetic moments directly apply to quantum spins. The Hamiltonian for a two-level system is introduced, and the expectation values for the magnetic moment are derived using the equation of motion. The paragraph explains that the quantum system's dynamics are characterized by rotation and precession, which is an exact result for quantum mechanics, valid for any spin. It also touches on the special case of spin-1/2 systems, which are analogous to two-level systems, and the implications for composite angular momentum in atoms. The discussion concludes with an example of Dicke superradiance, which involves a system of N two-level systems interacting with an external field.
📉 The Dynamics of Quantum Systems and the Landau-Zener Problem
This section of the script discusses the dynamics of quantum systems, particularly focusing on the Landau-Zener problem. It starts by examining the Hamiltonian for a two-level system with a splitting and a drive term, which is represented as a simple complex exponential. The script then explores the possibility of realizing this Hamiltonian in nature, either through an approximation or an exact realization. The discussion leads to the conclusion that the Hamiltonian can indeed be exactly realized, as it is derived from real fields without approximation. The paragraph concludes with a clicker question to gauge the understanding of whether this Hamiltonian is an idealization or an exact representation that can be found in nature.
🔬 Quantum Mechanical Hamiltonian for Spin-1/2 Systems
The script provides a detailed exploration of the quantum mechanical Hamiltonian for spin-1/2 systems. It begins by introducing the Hamiltonian for a two-level system with an energy splitting and a drive term, which is represented by a rotating magnetic field. The Hamiltonian is then expressed in terms of Pauli spin matrices, leading to a complex form involving the Rabi frequency and the detuning from resonance. The paragraph explains how the Hamiltonian can be rewritten in terms of spin operators, resulting in a form that includes a rotating field component. The discussion culminates in the derivation of the famous two-level Hamiltonian, which is a fundamental tool for analyzing the interaction of a two-level system with an electromagnetic field.
🌟 Dressed States and the Quantum Description of Electromagnetic Fields
This part of the script delves into the concept of dressed states and the quantum description of electromagnetic fields. It starts by addressing a question about the distinction between dressed states in the context of a fully quantized field and the current Hamiltonian's eigenstates and eigenenergies. The explanation clarifies that both the classical picture with an analog amplitude and the fully quantized picture with photon number states lead to the same solutions. The script then discusses the dressed atom picture and the coherent state description, highlighting the correspondence between the two in the limit of a large photon number. The discussion concludes with an emphasis on the importance of understanding both descriptions and the homework assignment that will involve writing down the general solution for the Hamiltonian.
🛠 Solving the Two-Level System Hamiltonian
The script describes the process of solving the Hamiltonian for a two-level system. It begins by discussing the unitary transformation that simplifies the Hamiltonian into a time-independent form, which is easier to solve. The transformation involves rotating the frame of reference, which is analogous to the approach taken in classical problems. The script then explains how the diagonal elements of the transformed Hamiltonian represent the detuning from the energy splitting of the two-level system. The discussion concludes with the observation that when the system is on resonance, the diagonal elements disappear, indicating that the system's energy levels are equally spaced.
🔬 Quantum Mechanical Aspects of Rapid Adiabatic Passage
This section of the script explores the quantum mechanical aspects of rapid adiabatic passage, focusing on the transition probabilities when the system is not fully adiabatic. It starts by presenting the Hamiltonian in a rotating framework, which allows for a time-independent representation. The script then discusses the energy levels of the system as a function of detuning and the effect of the Rabi frequency on the system's resonance. The discussion leads to the formulation of the Landau-Zener problem, which describes the quantum mechanical behavior of a system swept through an avoided crossing. The script concludes with a mention of the textbook result for the non-adiabatic transition probability, expressed as an exponential function involving the Landau-Zener parameter.
📉 The Landau-Zener Parameter and Transition Probabilities
The script delves deeper into the Landau-Zener parameter and the calculation of transition probabilities in the context of a diabatic sweep. It begins by explaining the concept of the Landau-Zener parameter as a ratio of the Rabi frequency squared to the sweep rate. The discussion then moves on to the perturbative approach to estimate the small probability of transition during a sweep that is not infinitely fast. The script emphasizes the importance of understanding this process, as it is commonly used in laboratory settings for transferring population between states. The paragraph concludes with a consideration of the effective time during the sweep and how it relates to the coherent build-up of amplitude in the second state.
🤔 Effective Time in Landau-Zener Crossing and Coherent Processes
In this final section, the script addresses the concept of effective time in the context of the Landau-Zener crossing and the nature of coherent processes. It starts by considering the source of incoherence in the system and concludes that the process is coherent due to the absence of factors that would lead to incoherent behavior. The script then discusses the importance of identifying the effective time during which the system is coherently driven, as this determines the transmission amplitude and the probability of transition. The discussion leads to a consideration of different possibilities for defining the effective time and concludes with the assertion that the effective time is related to the dephasing time, during which the system evolves coherently. The script wraps up with a brief mention of the homework and the next class meeting.
Mindmap
Keywords
💡Rapid Adiabatic Passage
💡Adiabatic Condition
💡Larmor Precession
💡Landau-Zener Parameter
💡Heisenberg Equation of Motion
💡Two-Level System
💡Rabi Frequency
💡Quantum Mechanical Hamiltonian
💡Dressed Atom Picture
💡Coherent State
💡Landau-Zener Problem
Highlights
Rapid adiabatic passage is a robust method for manipulating classical and quantum systems, particularly in inverting spin populations.
The adiabatic condition requires that the rotation of the effective magnetic field must be much slower than the precession of the spin.
A counterexample illustrates the importance of the adiabatic condition in maintaining alignment with the magnetic field.
The Landau-Zener parameter is introduced as a key factor in understanding quantum mechanical transitions during rapid adiabatic passage.
The Heisenberg equation of motion is used to derive the behavior of quantum systems with magnetic moments in an applied external magnetic field.
Quantum systems with magnetic moments precess in an external magnetic field, an exact result valid for any spin, not just spin-1/2.
The concept of Dicke superradiance is mentioned as an example of a system with N two-level systems interacting with an external field.
The Hamiltonian for a two-level system in a magnetic field is derived, providing a fundamental model for quantum mechanics.
The dressed atom Hamiltonian is introduced as a tool for calculating eigenstates and eigenenergies in oscillating fields of arbitrary strengths.
The dressed states in both the classical and quantized electromagnetic field descriptions are shown to be equivalent.
The Landau-Zener problem is discussed as a quantum mechanical description of sweeping through an avoided crossing.
The Landau-Zener parameter is derived from the quantum mechanical Hamiltonian, connecting classical and quantum descriptions of adiabaticity.
The probability of a non-adiabatic transition during a sweep is given by an exponential function involving the Landau-Zener parameter.
Perturbation theory is applied to estimate the small transition probability in the almost diabatic limit of the Landau-Zener crossing.
The effective time during a Landau-Zener sweep is identified as the time window where substantial amplitude is added to the second state coherently.
The connection between the effective time derived from perturbation theory and the exact result for the Landau-Zener probability is established.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: