Physics 59 Optical Instruments (3 of 20) The Microscope

Michel van Biezen
7 May 201312:02
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the intricate workings of a microscope, contrasting it with a telescope. It explains the dual-lens structure, with an objective lens and an eyepiece, and their short focal lengths. The script guides viewers through the process of calculating the microscope's magnification, considering both lenses and the object's placement relative to the focal points. It also discusses the impact of relaxed versus strained vision on magnification, ultimately revealing the formula to determine the microscope's total magnifying power.

Takeaways
  • 🔬 Microscopes, like telescopes, have two lenses: an objective lens in front and an eyepiece (IPS) in the back.
  • 🌀 Both lenses in a microscope typically have very short focal lengths compared to a telescope.
  • 📏 The magnification of a microscope is the product of the magnifications of the objective lens and the eyepiece.
  • 👀 The eyepiece acts like a magnifying glass, and its magnification can be calculated using the formula M2 = 25 / focal length of the eyepiece.
  • 🔍 For relaxed vision, the magnification of the eyepiece is 25 centimeters divided by the focal length of the eyepiece plus one.
  • 👁 For strained vision, the magnification is calculated without the addition of one, placing the image about 25 centimeters away from the observer.
  • 📐 The position of the object in a microscope is crucial for focusing and is usually placed just in front of the focal point of the objective lens.
  • 🔄 The brain perceives the image as coming from a point much further back, creating a virtual, magnified, and inverted image.
  • ⚖️ The magnification of the objective lens (M1) is calculated using the formula M1 = -(L - F_eyepiece) / F_objective, where L is the microscope length.
  • 🔢 The total magnification of the microscope is affected by the precise placement of the object, which can be adjusted using the lens equation.
  • 🔄 Adjusting the object placement from the focal point of the objective lens to a more accurate position changes the calculated magnification.
Q & A

  • What are the two lenses in a microscope called?

    -The two lenses in a microscope are called the objective lens, which is in the front, and the eyepiece (also known as the ocular lens), which is in the back.

  • Why are both the focal lengths of the lenses in a microscope typically very short?

    -Both the focal lengths of the lenses in a microscope are typically very short to allow for high magnification and to focus on very small objects placed close to the objective lens.

  • What is the relationship between the length of the microscope and the focal points of its lenses?

    -The length of the microscope should be such that there is a significant distance between the two focal points of the lenses, ensuring that the object is placed between them to form a clear image.

  • How is the position of the object related to the focal point of the first lens in a microscope?

    -In a microscope, the object is typically placed just in front of the focal point of the first lens, or the objective lens, to form an image that is then magnified by the eyepiece.

  • What is the formula for the magnification of a magnifying glass?

    -The magnification of a magnifying glass is given by the formula M = 25 cm / focal length of the eyepiece, for relaxed vision, or M = 25 / (focal length of the eyepiece + 1) for strained vision.

  • How does the brain perceive the magnified image in a microscope?

    -The brain perceives the magnified image in a microscope by interpreting the rays bending from the image formed by the first lens (objective lens) as coming from a virtual image that is much larger and inverted compared to the actual object.

  • What is the total magnification of a microscope?

    -The total magnification of a microscope is the product of the magnifications of the first lens (objective lens) and the second lens (eyepiece).

  • How is the magnification of the first lens (objective lens) calculated?

    -The magnification of the first lens is calculated using the formula m1 = - (L - F_eyepiece) / F_objective, where L is the length of the microscope, F_eyepiece is the focal length of the eyepiece, and F_objective is the focal length of the objective lens.

  • What adjustments are made to the position of the object for a more accurate image in a microscope?

    -To get a more accurate and focused image, the object is not placed exactly at the focal point of the objective lens but slightly in front of it, using the lens equation to determine the correct distance.

  • How does the final magnification of the microscope differ when considering the correct object distance?

    -When considering the correct object distance, the final magnification of the microscope is adjusted to account for the actual position of the object, which can result in a slightly lower magnification value than the initial approximation.

Outlines
00:00
🔬 Understanding Microscope Magnification

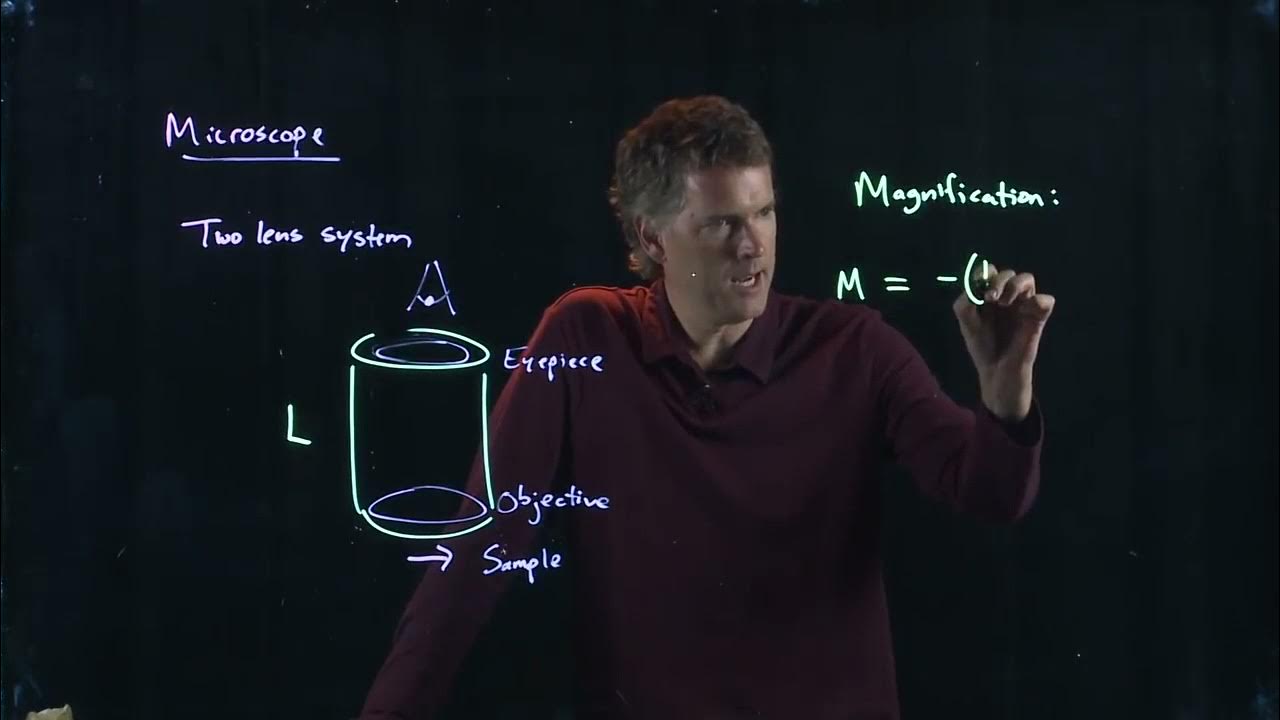
This paragraph introduces the basic concept of how a microscope works and the factors affecting its magnification. It explains that a microscope has two lenses: the objective lens at the front and the eyepiece (IPS) at the back, both with short focal lengths. The objective lens is set to have a focal length of 5 cm, while the eyepiece has a focal length of 2 cm. The setup involves placing the lenses such that their focal points are far apart, with the microscope's total length (L) being 20 cm. The object to be magnified is typically placed just in front of the objective lens's focal point. The paragraph also begins to explain the process of finding the magnification of a microscope, which involves the product of the magnifications of both lenses.

05:03
📐 Calculating Microscope Magnification

This paragraph delves deeper into the calculation of a microscope's magnification. It starts by discussing the magnification of the eyepiece, which can be calculated using relaxed or strained vision, resulting in magnifications of 12.5x for relaxed vision and 13.5x for strained vision. The paragraph then moves on to calculate the magnification of the objective lens, initially using an approximation by placing the object at the focal length of the objective lens. This leads to a magnification of -45x, indicating an inverted image that is 45 times larger than the object. However, the paragraph acknowledges that this is an idealized scenario and that the actual placement of the object is slightly in front of the focal point, affecting the magnification. It introduces the lens equation to find the correct object placement for a focused image and recalculates the magnification of the objective lens, resulting in a new value of -2.6x.

10:05
🔍 Refining Microscope Magnification Calculation

The final paragraph refines the understanding of microscope magnification by adjusting the calculation to account for the correct placement of the object. It explains that the magnification is the product of the magnifications of the two lenses and that the second lens acts as a simple magnifying glass. The paragraph corrects the initial approximation by using the lens equation to find the precise object distance (s) and then recalculates the magnification of the objective lens, taking into account this correct distance. The new calculation results in a magnification of -2.6x, which is less than the initial approximation, reflecting a more accurate representation of the microscope's magnifying power.

Mindmap
Keywords
💡Microscope
A microscope is an instrument used to observe objects that are too small to be seen by the naked eye. It is central to the video's theme, which is to explain how a microscope works. The script describes the microscope's components and how they contribute to magnification, such as the objective lens and the eyepiece.
💡Objective Lens
The objective lens is the front lens of a microscope, responsible for the initial magnification of the object being observed. In the script, it is mentioned as having a focal length of 5 centimeters, which is a key parameter in calculating the microscope's total magnification.
💡Eyepiece (Ocular Lens)
The eyepiece, or ocular lens, is the lens at the back of the microscope through which the observer views the magnified image. The script explains its role in the final stage of magnification, with a focal length of 2 centimeters, and how it functions like a magnifying glass.
💡Focal Length
Focal length is the distance over which light rays parallel to the optical axis converge or appear to diverge when passing through a lens. The script discusses the focal lengths of both the objective and eyepiece lenses, which are crucial for understanding the microscope's magnification capabilities.
💡Magnification
Magnification refers to the process of making small objects appear larger for better visibility. The video's main message revolves around explaining how to calculate the magnification of a microscope, which is done by multiplying the magnifications of the objective lens and the eyepiece.
💡Optical Axis
The optical axis is an imaginary line that passes through the center of a lens system and is along which light rays travel. The script mentions rays coming through parallel to the optical axis and bending upon passing through the lenses, which is essential for image formation in a microscope.
💡Virtual Image
A virtual image is one that appears to be located behind the lens system and cannot be projected onto a screen. The script explains that the final image formed by the microscope is a virtual image, which is seen as large and inverted by the observer's brain.
💡Lens Equation
The lens equation, 1/f = 1/s + 1/s', relates the focal length (f) of a lens to the object distance (s) and the image distance (s'). The script uses this equation to determine the correct placement of the object for a focused image in the microscope.
💡Relaxed Vision vs. Strain Vision
Relaxed vision and strain vision refer to the observer's eye conditions when using the microscope. The script explains that the magnification calculation for the eyepiece can differ based on whether the observer's vision is relaxed or strained, affecting the perceived distance of the image.
💡Inverted Image
An inverted image is one where the top and bottom of the object are reversed in the view. The script mentions that the image formed by the microscope is inverted, which is a common characteristic of microscopes and important for understanding the orientation of the observed specimen.
💡Focal Point
The focal point is the location where light rays converge after passing through a lens or where they appear to diverge from. The script discusses the importance of the focal point in relation to both the objective and eyepiece lenses, particularly in the context of image formation and magnification.
Highlights

Microscopes have two lenses, the objective lens in the front and the eyepiece (IPS) in the back, both with short focal lengths.

The setup involves placing the lenses far enough apart to have a large distance between the two focal points.

The length of the microscope (L) is an important factor in calculating magnification, set at 20 centimeters in the example.

Objects for microscopic observation are typically very small and placed just in front of the first lens's focal point.

The magnification of a microscope is the product of the magnifications of both the objective and eyepiece lenses.

The eyepiece acts like a magnifying glass with magnification calculated as 25 cm divided by its focal length.

Two types of vision are considered for magnification calculation: relaxed and strained vision.

For the given example, the eyepiece's magnification is 12.5 times with relaxed vision and 13.5 times with strained vision.

The magnification of the objective lens is calculated using the formula m1 = -s'/s, where s' is the image distance and s is the object distance.

The image formed by the objective lens is just inside the focal point of the eyepiece, at L - F_eyepiece.

An approximation is made by initially placing the object at the focal length of the objective lens for simplicity.

The actual object placement is determined using the lens equation 1/F = 1/s + 1/s'.

Adjusting the object placement affects the magnification, leading to a more accurate calculation.

The final magnification of the microscope is recalculated using the correct object distance and lens focal lengths.

The magnification of the objective lens is recalculated as -2.6 times, reflecting a more accurate value.

The overall magnification of the microscope is a combination of the magnifications of both lenses, considering the correct object placement.

The process demonstrates the complexity of calculating the magnification for a microscope compared to a telescope.

Understanding the correct placement of the object and the use of both lenses' focal lengths is crucial for accurate magnification.

Transcripts

Browse More Related Video

The Microscope | Physics with Professor Matt Anderson | M28-12

Focal Length of Eyepiece in a Microscope | Physics with Professor Matt Anderson | M28-22

The Telescope | Physics with Professor Matt Anderson | M28-13

Physics 59 Optical Instruments (1 of 20) Magnifying Glass

Physics 59 Optical Instruments (2 of 20) The Telescope

How telescopes work | Class12 (India) | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MicroscopeMagnificationTutorialLens MechanicsOpticsScience EducationMicroscopy BasicsFocal LengthVirtual ImageInverted ImageImaging Techniques