Scales of Measurement - Nominal, Ordinal, Interval, Ratio (Part 2) - Introductory Statistics
TLDRThis video script discusses the four scales of measurement: nominal, ordinal, interval, and ratio. It explains that nominal scales differentiate without inherent order, ordinal scales establish rank without equal intervals, interval scales have equal differences but lack a true zero, and ratio scales have both meaningful ratios and a true zero point. Examples are provided to illustrate these concepts, such as weight for ratio and temperature for interval, emphasizing the importance of understanding the nature of data when measuring.
Takeaways
- 📏 Ratio Scales: Have meaningful ratios and a true zero point, indicating the absence of a property, such as weight in pounds where 10 pounds is twice as much as 5 pounds.
- 🌡️ Interval Scales: Feature equal intervals between points but do not have a true zero point, like temperature where zero degrees Fahrenheit is very cold, not an absence of heat.
- 🏁 Ordinal Scales: Indicate order but not the magnitude of differences between categories, such as the position in a race where the gap between first and second might be different from second and third.
- 🔢 Nominal Scales: Used for categorization without any intrinsic order or quantitative difference, like baseball uniform numbers which differentiate players but do not imply any ranking or measurement.
- 🔄 Ratio vs Interval: While both have meaningful differences, the key distinction is the presence of a true zero point and meaningful ratios in ratio scales, unlike in interval scales.
- ❗️ True Zero Point: Essential for ratio scales, it represents the complete absence of a property, which is not the case with interval scales like temperature.
- 🏋️♂️ Example of Ratio: Weight in pounds, where adding two equal weights results in a sum that maintains the ratio, unlike with temperature.
- 🏃♂️ Example of Ordinal: Placing in a race, where the order is known but the differences between positions are not necessarily equal or quantifiable.
- 👕 Example of Nominal: Baseball uniform numbers, which serve only to differentiate and do not represent any measurable or ordered quantity.
- ❌ Non-Quantitative Differences: In ordinal scales, differences between categories are not quantitative, unlike in ratio or interval scales.
- 🔑 Understanding Scales: The script emphasizes the importance of understanding the type of scale being used to correctly interpret and compare data.
Q & A
What is the main difference between interval and ratio scales?
-The main difference between interval and ratio scales is that ratio scales have meaningful ratios and a true zero point, which represents the absence of the property being measured. Interval scales have equal intervals between points but do not necessarily have a true zero point or meaningful ratios.
Can you provide an example of a ratio scale?
-An example of a ratio scale is weight measured in pounds. Here, 10 pounds is twice as much as 5 pounds, indicating a meaningful ratio, and 0 pounds represents no weight or an absence of weight.
What is the significance of a 'true zero point' in measurement scales?
-A 'true zero point' in measurement scales signifies that the zero value represents the complete absence of the property being measured. It is a fundamental characteristic of ratio scales.
How does the concept of 'ratio differences' apply to the weight example mentioned in the script?
-In the weight example, the concept of 'ratio differences' is applied by showing that the weight of an object can be doubled or halved, and these ratios are meaningful. For instance, 10 pounds is twice as heavy as 5 pounds, which is a meaningful comparison.
What is the difference between ordinal and interval scales in terms of the significance of the differences between categories?
-In ordinal scales, the differences between categories do not necessarily have to be equal or meaningful, as in the example of finishing places in a race. In contrast, interval scales have equal intervals between all points on the scale, such as a one-degree difference being the same at all points for temperature.
Can you explain why temperature is considered an interval scale rather than a ratio scale?
-Temperature is considered an interval scale because it has equal intervals between points and does not have a true zero point that represents the absence of the property (coldness or heat). For example, 0 degrees Fahrenheit does not mean there is no coldness, it is actually very cold, indicating that zero does not represent an absence of temperature.
What is an example of an ordinal scale and how does it differ from interval and ratio scales?
-An example of an ordinal scale is the finishing places in a race (first, second, third). It differs from interval and ratio scales because it only reflects order and does not have equal intervals or meaningful ratios between the categories.
How does the script differentiate between nominal and ordinal scales using the example of baseball uniform numbers?
-The script differentiates between nominal and ordinal scales by explaining that baseball uniform numbers are nominal because they only differentiate between players without any inherent order or meaningful differences. In contrast, ordinal scales have a clear order but do not have equal intervals or meaningful ratios.
Why are baseball uniform numbers not considered to be on an interval or ratio scale?
-Baseball uniform numbers are not considered to be on an interval or ratio scale because they do not have equal intervals between them, and there are no meaningful ratios or a true zero point. The numbers are simply used to identify players and do not represent measurable quantities.
What is the key takeaway from the script regarding the comparison of different measurement scales?
-The key takeaway from the script is understanding the distinct characteristics of nominal, ordinal, interval, and ratio scales. Each scale type has specific properties regarding order, equal intervals, meaningful ratios, and the presence or absence of a true zero point.
How can the concepts explained in the script be applied to real-world scenarios for better data analysis?
-The concepts explained in the script can be applied to real-world scenarios by ensuring that the appropriate scale is used for the type of data being analyzed. This helps in making accurate comparisons, understanding the significance of differences, and drawing meaningful conclusions from the data.
Outlines
📊 Understanding Ratio, Interval, Ordinal, and Nominal Scales
This paragraph delves into the characteristics and differences between ratio, interval, ordinal, and nominal scales of measurement. It explains that ratio scales have meaningful ratios and a true zero point, exemplified by weight in pounds where zero indicates the absence of weight. Interval scales, such as temperature, have equal intervals but no true zero point, meaning zero does not signify the absence of the property. Ordinal scales, like race placements, have order but the differences between categories are not necessarily equal, highlighting the distinction from interval scales. Nominal scales, such as baseball uniform numbers, differentiate without any inherent order or quantitative difference, and do not have a true zero point. The paragraph emphasizes the importance of distinguishing between these scales to accurately interpret data.
🏅 Conclusion on Measurement Scales
The second paragraph concludes the discussion on measurement scales, summarizing the key points made about ratio, interval, ordinal, and nominal scales. It reiterates the unique features of each scale type and their applications. The paragraph serves as a wrap-up, reinforcing the importance of understanding these scales for proper data analysis and interpretation. It ends with a note of thanks to the viewers for watching, indicating the end of the video script.
Mindmap
Keywords
💡Ratio Differences
💡Interval Scale
💡Ordinal Scale
💡True Zero Point
💡Nominal Scale
💡Measurement Scales
💡Weight in Pounds
💡Zero Degrees
💡Race Example
💡Baseball Uniform Numbers
💡Scales of Measurement
Highlights
Ratio differences are meaningful, similar to interval scales, but also include meaningful ratios and a true zero point.
A true zero point indicates the absence of the property, such as 0 inches representing no length.
Weight in pounds is an example of a ratio scale, where 10 pounds is twice as much as 5 pounds.
Interval scales have equal intervals between points on the scale, like temperature where a one-degree difference is consistent.
Ordinal scales have order but not necessarily equal intervals, as in the difference between finishing places in a race.
The difference between first and second place in a race may not be the same as between second and third, making it ordinal.
If only the order of finish (e.g., first, second, third) is known, it is a classic example of ordinal data.
Ratio scales require meaningful ratios and a true zero point, which represents the absence of the property.
Temperature is an interval scale, not a ratio, because zero degrees does not represent an absence of cold.
Combining two 40-degree days does not result in an 80-degree day, showing that temperature ratios are not meaningful.
Nominal scales differentiate without order or meaningful differences, such as baseball uniform numbers.
Uniform numbers do not have a meaningful order or intervals, and ratios are not applicable.
A zero uniform number does not imply an absence of a player, distinguishing it from other scales.
Understanding the differences between nominal, ordinal, interval, and ratio scales is crucial for proper data analysis.
Each scale type has distinct characteristics that define how data can be interpreted and used.
The transcript provides clear examples to differentiate between the four types of measurement scales.
The explanation of scales helps in understanding when to apply each type in various contexts.
Transcripts
Browse More Related Video

Scales of Measurement - Nominal, Ordinal, Interval, & Ratio Scale Data
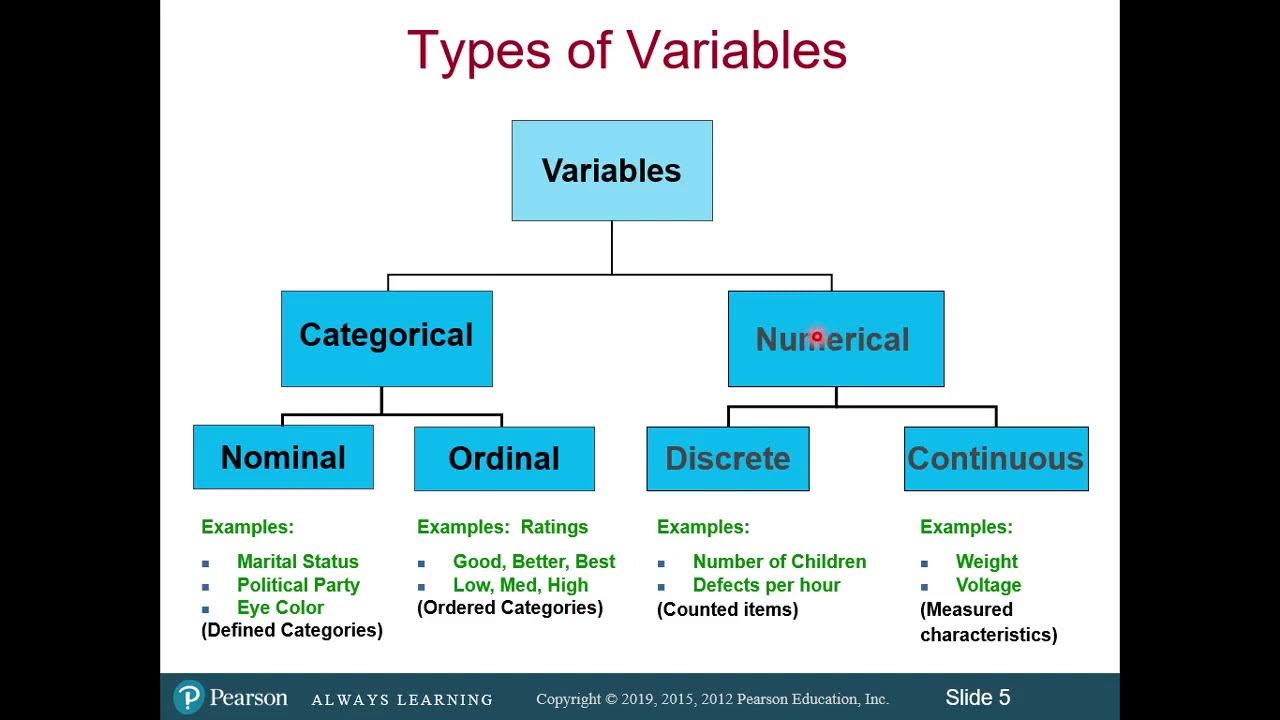
Classification of Variables and Types of Measurement Scales

Scales of Measurement - Nominal, Ordinal, Interval, Ratio (Part 1) - Introductory Statistics

Nominal, Ordinal, Interval & Ratio Data: Simple Explanation With Examples

Data Types - Levels of Data Measurements - Nominal Ordinal Interval Ratio | Statistics | Research

Introduction to Levels of Measurement: Nominal, Ordinal, Interval, Ratio
5.0 / 5 (0 votes)
Thanks for rating: