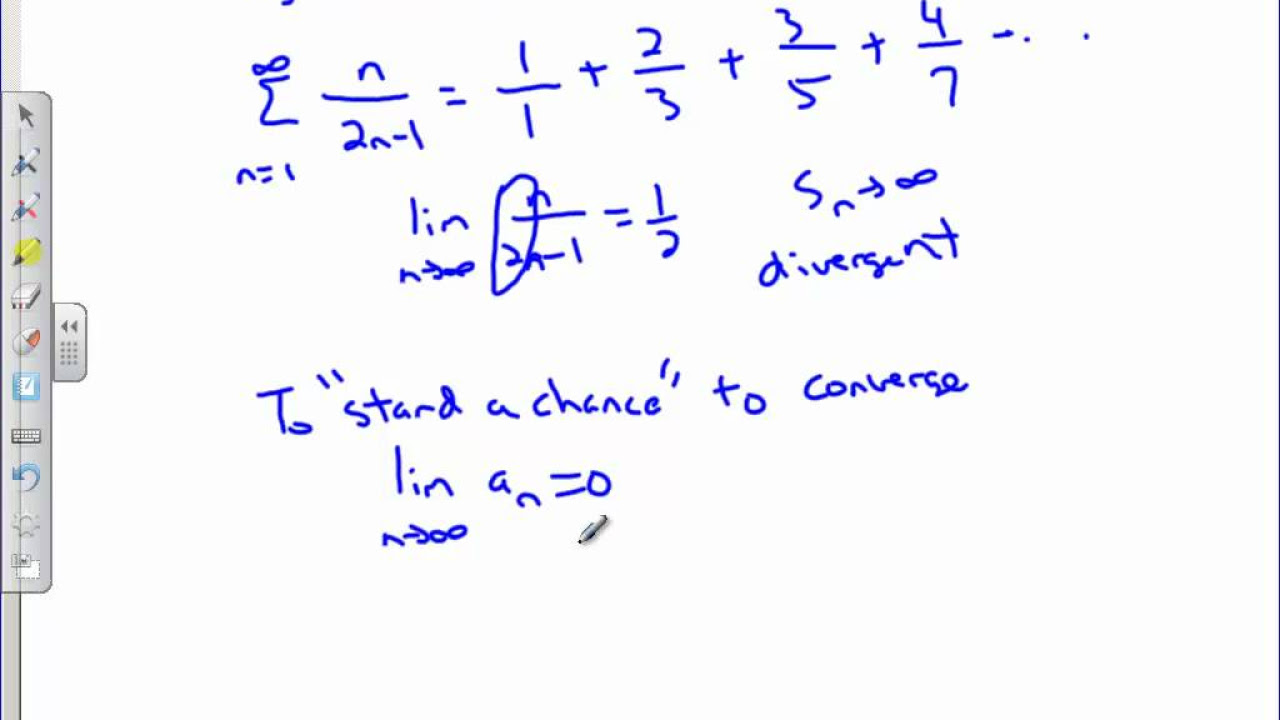Lesson 17 - Series (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis advanced calculus tutorial segment focuses on the foundational concepts of sequences and series, specifically introducing the concept of a series. The instructor emphasizes that a series is the sum of the terms in a sequence, and the main interest lies in determining whether the sum converges or diverges. The video begins with an explanation of series, relating it to sequences, and then discusses the importance of understanding the behavior of sequence elements as they approach infinity. The instructor also mentions that they will cover necessary theorems before diving into problem-solving to ensure a solid understanding of the concepts.

Takeaways
  • πŸ“š The section is focused on introducing the concept of series in the context of advanced calculus.
  • πŸ”— The topic of series is closely related to sequences, which was the subject of the previous section.
  • 🚫 The instructor emphasizes that examples will not be introduced immediately to avoid confusion, as they require understanding of upcoming theorems first.
  • πŸ“ The script mentions that series are formed by adding up the terms of a sequence.
  • πŸ”’ A sequence is a list of numbers, while a series is the sum of those numbers.
  • 🌐 The behavior of sequence terms as they approach infinity is a key consideration in determining the behavior of a series.
  • πŸ’₯ If a sequence diverges to infinity, its corresponding series will also likely diverge.
  • πŸ’Ύ However, if sequence terms approach zero quickly enough, it's possible for the series to converge.
  • πŸ” The main interest in this section is to determine whether the sum of a series can converge or not.
  • πŸ“š The instructor plans to present and explain theorems that are foundational to understanding series before moving on to problem-solving.
  • πŸ€“ The section aims to build on the foundation laid by the study of sequences and apply it to the concept of series.
Q & A

  • What is the main topic of this section of the advanced calculus tutorial?

    -The main topic of this section is an introduction to series, which is a continuation from the topic of sequences.

  • Why can't the tutor dive into examples right away when teaching about series?

    -The tutor cannot dive into examples right away because students would get confused without first understanding the necessary theorems that will be used in solving problems related to series.

  • What is the relationship between a sequence and a series?

    -A sequence is a list of numbers separated by commas, while a series is the sum of those numbers in the sequence.

  • What is the primary interest when studying series in this section?

    -The primary interest is to determine whether the sum of the elements in a series can converge or not.

  • What happens to the sum of a series if the elements of the original sequence increase indefinitely?

    -If the elements of the original sequence increase indefinitely, the sum of the series will also increase indefinitely, leading to divergence.

  • How does the behavior of elements in a sequence affect the convergence of a series?

    -If the elements of a sequence approach zero quickly enough, it might be possible for the series to converge, despite having an infinite number of terms.

  • What is the tutor's strategy for teaching the concept of series in this section?

    -The tutor's strategy is to first present and explain the necessary theorems before diving into problem-solving to ensure a solid understanding of the concepts.

  • What is the significance of limits in the context of sequences and series?

    -Limits are significant as they help in understanding the behavior of sequences and series, especially when considering terms that approach infinity.

  • What is the difference between a sequence that blows up to infinity and a convergent series?

    -A sequence that blows up to infinity means its terms keep increasing without bound, while a convergent series is one where the sum of its terms approaches a finite value.

  • Why is it important to understand theorems before solving series problems?

    -Understanding theorems is important because they provide the foundational knowledge required to solve series problems effectively and avoid confusion.

  • How does the tutor plan to make the theorems easier to understand and remember?

    -The tutor plans to explain the theorems in a different way than what might be found in textbooks, aiming to make them easier to understand and remember.

Outlines
00:00
πŸ“š Introduction to Series in Advanced Calculus

This paragraph introduces the topic of series within the context of advanced calculus. It explains that a series is essentially the sum of the terms in a sequence, which is a list of numbers. The speaker apologizes for not being able to provide examples immediately, as they first need to teach the necessary theorems that underpin the understanding of series. The paragraph sets the stage for the foundational concepts that will be explored in the subsequent sections, emphasizing the importance of understanding sequences before diving into series. It also hints at the main focus of the series section, which is to determine whether the sum of an infinite number of terms can converge to a finite value.

Mindmap
Keywords
πŸ’‘Series
A series in the context of calculus is the sum of the terms of a sequence. It is a fundamental concept in the video, as it builds upon the idea of sequences, which are simply lists of numbers. The series is formed by adding up these numbers. For example, if you have a sequence of 1/2, 1/4, 1/8, ..., the corresponding series would be the sum of these fractions. The video discusses how the behavior of the terms in a series can lead to either divergence (the sum gets infinitely large) or convergence (the sum approaches a finite value), which is a central theme of the tutorial.
πŸ’‘Sequence
A sequence is an ordered list of numbers, which can be finite or infinite. In the video, sequences are introduced as the precursor to series, where each term in the sequence is simply listed, separated by commas. The behavior of these terms as they approach infinity is a key point of interest, as it influences whether the series formed from these terms will converge or diverge. The script uses sequences like 1, 1/2, 1/4, ... to illustrate this concept.
πŸ’‘Convergence
Convergence in calculus refers to the property of a series where the sum of its terms approaches a finite, non-infinite value as more terms are added. The video emphasizes the importance of determining whether a series converges, as this is a critical aspect of analyzing series. For instance, if the terms of a sequence approach zero quickly enough, their sum might converge to a specific number, which is a key point of interest in the tutorial.
πŸ’‘Divergence
Divergence is the opposite of convergence. It occurs when the sum of the terms in a series increases without bound, heading towards infinity. The video script mentions divergence in the context of series where the terms of the original sequence become larger and larger, causing the series to also increase indefinitely, which is an undesirable property in many mathematical applications.
πŸ’‘Theorems
Theorems are formal statements in mathematics that are proven based on previously established statements and accepted rules of inference. In the video, the tutor mentions the need to introduce and explain certain theorems before diving into examples. These theorems are essential for understanding the conditions under which a series converges or diverges and are foundational to the study of series in advanced calculus.
πŸ’‘Limits
Limits are a fundamental concept in calculus that describe the behavior of a function or sequence as the input approaches a certain value. In the context of the video, limits are used to analyze the behavior of the terms in a sequence as they approach infinity, which is crucial for determining the convergence or divergence of a series. The script discusses how terms approaching zero can affect the convergence of a series.
πŸ’‘Infinite
The concept of infinity in mathematics refers to an unbounded quantity that is larger than any finite number. In the video, infinity is used to describe the behavior of sequences and series that do not have an end. The tutor explains how sequences that 'blow up' to infinity can affect the series formed from them, often leading to divergence.
πŸ’‘Terms
In the context of sequences and series, terms refer to the individual numbers or expressions that make up the sequence. The video script uses the term 'elements' interchangeably with 'terms' to describe the components of a sequence that are added together to form a series. Understanding the properties of these terms is essential for analyzing the behavior of the series.
πŸ’‘Behavior
Behavior in this mathematical context refers to how the terms of a sequence or the sum of a series change as you consider more and more terms, especially as you approach infinity. The video emphasizes analyzing the behavior of sequences and series to determine their convergence or divergence. For example, the behavior of terms approaching zero is crucial for the potential convergence of a series.
πŸ’‘Tutorial
A tutorial is an instructional lesson or guide, often designed to teach a specific topic or skill. In the script, the term 'tutorial' is used to describe the nature of the video, which is intended to educate viewers on the topic of series in advanced calculus. The tutorial approach is meant to provide foundational knowledge and guide learners through the concepts and theorems before tackling problems.
Highlights

Introduction to series as a continuation of the sequence topic.

Series defined as the sum of the terms in a sequence.

Explanation of the importance of understanding sequences before series.

The necessity of learning theorems before solving series problems.

The concept that a series is the summation of sequence elements.

Behavior of sequence elements as they approach infinity.

The possibility of a series diverging if sequence elements increase without bound.

Potential for series convergence if sequence elements approach zero quickly enough.

The main focus of the section: determining if a series converges or diverges.

The importance of limits in analyzing sequences and series.

The transition from examining individual sequence elements to their sum in a series.

The upcoming exploration of different theorems related to series.

The need for a foundational understanding before applying theorems.

The approach of teaching theorems before diving into problem-solving.

The goal of making theorems easier to understand and remember.

An apology for not starting with examples to avoid confusion.

Theι’„ε‘Š of a big picture overview of the section on series.

Transcripts

Browse More Related Video

Lesson 18 - Integral Test (Calculus 2 Tutor)

Geometric Series (Precalculus - College Algebra 72)

Calculus BC – 10.1 Defining Convergent and Divergent Infinite Series

Calculus Nth Term Test

Convergence and Divergence: The Return of Sequences and Series

Lesson 21 - Ratio And Root Test (Calculus 2 Tutor)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Advanced CalculusSeries IntroductionSequence AnalysisInfinite SumsConvergenceDivergenceTheoremsEducational ContentMathematics TutorConcept Clarification