Lesson 21 - Ratio And Root Test (Calculus 2 Tutor)
TLDRThis advanced calculus tutorial focuses on the study of sequences and series, particularly the ratio and root tests for series convergence. The instructor emphasizes that there is rarely one method to solve a problem, encouraging students to be flexible in their approach. The video begins with definitions and theorems, including the concept of absolute convergence, which is a key component in the ratio and root test theorems. The goal is to determine if an infinite series of numbers converges to a unique number. The instructor advises students to keep an open mind and not to limit themselves to a single method, as different problems may require different approaches.
Takeaways
- 📚 The section is focused on completing the study of sequences and series, convergence, and limits, specifically discussing the ratio and root tests for series convergence.
- 🛠️ The presenter emphasizes that there is rarely one way to solve a problem in calculus and encourages students to be flexible with the methods they apply.
- 💡 The 'light bulb moment' is highlighted as a key realization for students to connect different methods they've learned to determine convergence.
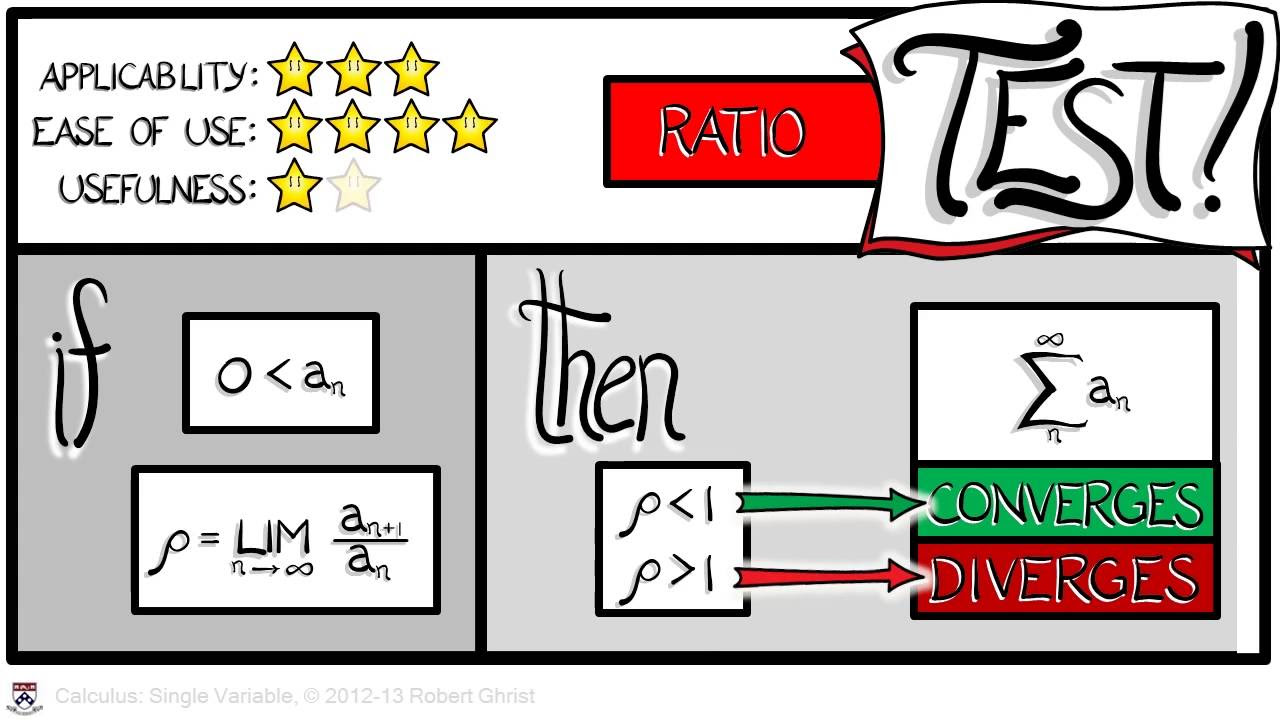
- 🔍 The ratio test and the root test are introduced as methods to determine if a series converges, and the presenter promises to show how to apply these tests.
- 📘 The importance of understanding definitions and theorems is stressed as a prerequisite for solving problems effectively.
- 🔢 Absolute convergence is defined as a series where the series of absolute values of the terms is convergent, which is a key concept for the ratio and root test theorems.
- 📝 The series is denoted with a summation symbol, and absolute convergence is indicated by adding 'absolutely' before 'convergent'.
- 🤔 The presenter encourages students to think beyond the methods taught in class, as different problems may require different approaches.
- 📚 The section will start with definitions and theorems before moving on to problem-solving, which is a common structure in mathematical teaching.
- 🧩 The analogy of integration with sines and cosines is used to illustrate the idea that there are multiple ways to approach a problem in calculus.
- 🎯 The goal of studying series convergence is to determine if an infinite series of numbers adds up to a unique number.
Q & A
What is the main topic of this section of the advanced calculus tutorial?
-The main topic of this section is the ratio and root test for series convergence in advanced calculus.
Why is it important to understand different methods for solving problems in this section?
-It is important to understand different methods because there is rarely one way to solve a problem, and being familiar with various methods can help you determine if a series converges or not.
What does the instructor suggest students should do when solving problems in this section?
-The instructor suggests that students should not limit themselves to a single method but keep an open mind to apply different methods they have learned in the past.
What is the significance of the 'ratio test' and 'root test' in this section?
-The ratio test and root test are significant because they are methods used to determine the convergence of a series, and they will be demonstrated through problems in the tutorial.
What is meant by 'series convergence' in the context of this tutorial?
-Series convergence refers to the process of determining if an infinite series of numbers adds up to a unique number, despite having an infinite number of terms.
Can you define 'absolute convergence' as mentioned in the script?
-Absolute convergence is defined as a series where the series of absolute values of the terms is convergent. It means if you take the absolute value of each term and sum them, the result converges to a number.
Why is absolute convergence important in the context of the ratio and root test theorems?
-Absolute convergence is important because it is a condition used in the ratio and root test theorems to determine if a series converges, and it provides a stronger guarantee of convergence than simple convergence.
What does the instructor mean by 'pigeonhole' in the context of solving problems?
-The instructor uses 'pigeonhole' as a metaphor to caution against limiting oneself to a single method or approach when solving problems, emphasizing the importance of flexibility and creativity.
How does the instructor plan to introduce the concepts of ratio and root tests?
-The instructor plans to introduce the concepts of ratio and root tests by first defining key terms and theorems and then demonstrating their application through problems.
What is the relationship between the series convergence and the absolute convergence as defined in the script?
-The relationship is that a series is said to be absolutely convergent if the series of the absolute values of its terms is convergent, which is a stronger condition than simple convergence.
Outlines
📚 Introduction to Ratio and Root Tests for Series Convergence
This paragraph introduces the topic of the video, which is the study of sequences and series, specifically focusing on the ratio and root tests for series convergence. The speaker emphasizes the importance of understanding multiple methods for solving problems, as there is rarely a single approach. They encourage students to be flexible in their problem-solving strategies, as different methods may be applicable depending on the problem at hand. The paragraph sets the stage for definitions and theorems that will be discussed later, with the ultimate goal of applying these concepts to determine the convergence of series.
Mindmap
Keywords
💡Advanced Calculus
💡Sequences
💡Series
💡Convergence
💡Ratio Test
💡Root Test
💡Definitions
💡Theorems
💡Absolute Convergence
💡Problem Solving
💡Integral Test
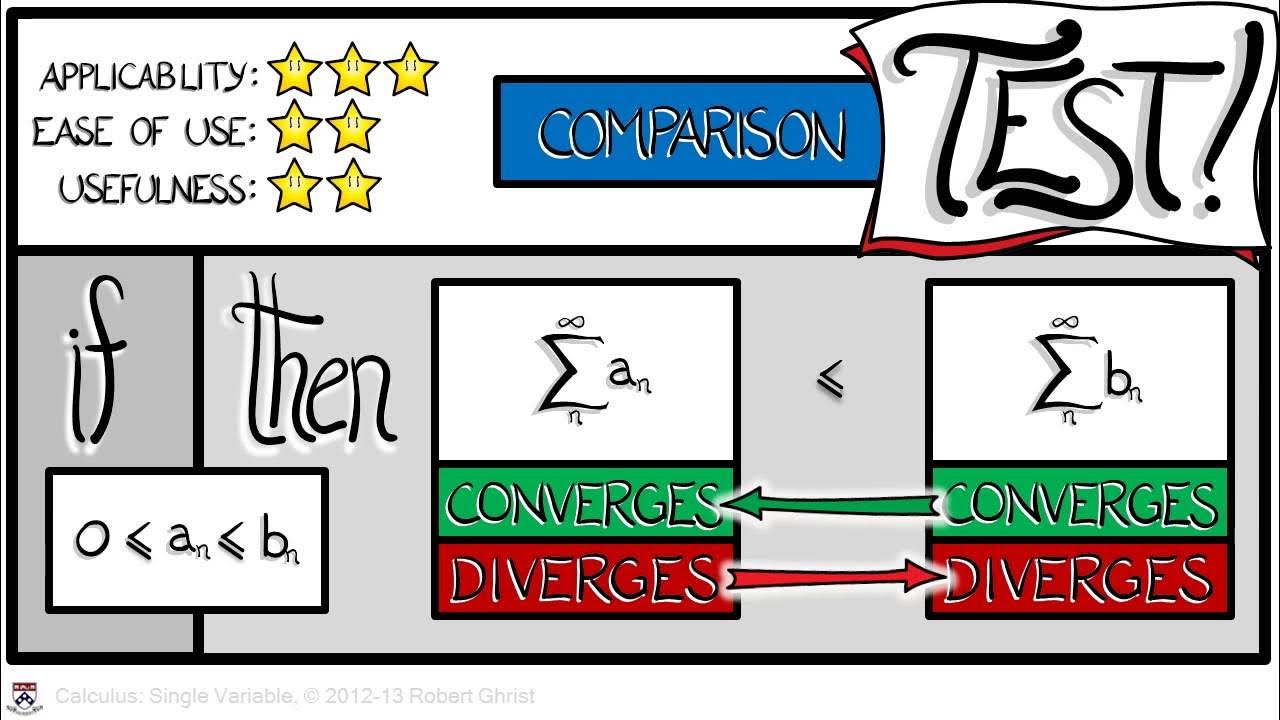
💡Comparison Test
Highlights
Introduction to the advanced calculus section focusing on sequences, series, convergence, and limits.
Explanation of the ratio and root tests for series convergence.
Emphasis on the importance of understanding multiple methods for problem-solving in calculus.
The concept that there is rarely one way to solve a calculus problem.
The potential for using integral tests and comparison tests alongside the ratio and root tests.
Encouragement to not limit oneself to a single method when approaching problems.
Introduction to the definition of series convergence and its significance.
The definition of absolute convergence and its role in the ratio and root test theorems.
Clarification that absolute convergence means the series of absolute values of the terms is convergent.
The importance of recognizing when a series can be positive or negative and still converge.
The process of determining if an infinite series of numbers converges to a unique number.
The significance of absolute convergence in the context of series convergence.
The practical application of absolute convergence in mathematical proofs and problem-solving.
A reminder that understanding the definitions and theorems is crucial for solving problems.
The anticipation of a 'light bulb' moment when applying different methods to determine convergence.
The analogy of having a 'tool bag' of methods to apply during tests and problem-solving.
The expectation that students will recognize the applicability of different methods to various problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: