Lecture 18: Getting Off the Line Motion in Space
TLDRIn this episode of 'Change in Motion: Calculus Made Clear,' the host explores the complexities of motion beyond straight lines, delving into calculus concepts such as derivatives and integrals. The video explains how to calculate instantaneous velocity and distance traveled for objects moving in two-dimensional space, using the example of a baseball's trajectory and a car's path. The host demonstrates how velocity is a combination of horizontal and vertical components, and how integrals can be used to find the total distance of a curved path. The lecture concludes with a proof of the Pythagorean theorem, emphasizing the universality of mathematical principles.
Takeaways
- 🚗 Cars and other objects often move in complex ways, not just in straight lines. The video discusses how calculus can be used to analyze motion in multiple dimensions.
- 📚 The concepts of derivatives and integrals, initially developed for simple cases like a car moving in a straight line, can be extended to more complex scenarios involving multiple degrees of freedom.
- 📏 To understand an object's motion, we can ask where it is at each moment, which involves considering its position in three spatial dimensions or two dimensions in the case of a flat plane.
- 🧭 Key questions about motion include the direction and speed of the moving object at any given time, which together define its velocity.
- 🛣 Calculus can help determine the distance traveled by an object, even when it moves along a curved path, by breaking the path into small straight segments and summing them up.
- 🏞 The video uses the example of a baseball's trajectory to illustrate how calculus can determine both the height and horizontal distance of the ball over time.
- 🔢 The velocity of an object moving in two dimensions can be found by combining its horizontal and vertical velocities using the Pythagorean theorem.
- 🚘 The video provides an example of a car moving along a specific path defined by mathematical functions for its x and y coordinates over time.
- 📉 The integral is used to find the total distance traveled by the car along its path, by integrating the speed of the car over the time interval of its journey.
- 📏 The Pythagorean theorem, essential for calculating the resultant velocity, is proven using geometric assembly of squares and triangles.
- 🌏 The video concludes with a cultural note on the universality of mathematics, referencing an Indian mathematician's proof of the Pythagorean theorem.
Q & A
What is the main theme of the 'Change in Motion: Calculus Made Clear' lecture?
-The main theme of the lecture is to extend the concepts of calculus, specifically derivatives and integrals, from simple scenarios like a car moving in a straight line to more complex situations involving motion with multiple degrees of freedom, such as a car turning or a mosquito flying in three dimensions.
Why do cars not always drive on straight lines according to the lecture?
-Cars do not always drive on straight lines because they often need to turn around and move in various interesting ways, which involves changes in direction and speed, making the motion more complex than simple straight-line movement.
What is the significance of extending calculus concepts from simple to complex scenarios?
-The significance of extending calculus concepts from simple to complex scenarios is that it allows for the application of these concepts to real-world problems that are not limited to one-dimensional motion. This helps in understanding and solving problems involving multi-dimensional motion, such as the trajectory of a projectile or the path of a planet.
What are the two main questions related to the motion of an object that the lecture discusses?
-The two main questions related to the motion of an object discussed in the lecture are: 1) In what direction is the moving object going at every instant of time? and 2) How fast is it going?
How does the lecture define velocity in the context of motion?
-In the context of motion, the lecture defines velocity as a vector quantity that includes both the speed (how fast) and the direction of an object's motion. It is derived from the combination of the object's velocity in different spatial dimensions.
What is the concept of a vector-valued function in the context of the lecture?
-A vector-valued function in the context of the lecture refers to a function where for every time 't', there are two different values associated with it, typically the x and y coordinates of an object's position in space. This is used to describe the motion of an object in two dimensions.
How does the lecture use the example of a baseball to illustrate the concept of velocity in two dimensions?
-The lecture uses the example of a baseball flying through the air to illustrate the concept of velocity in two dimensions. It explains that the baseball has a horizontal velocity component and a vertical velocity component. By using the Pythagorean theorem, the lecture shows how to combine these components to find the total velocity or speed of the baseball at any given time.
What is the challenge posed by the lecture for the analysis of motion?
-The challenge posed by the lecture for the analysis of motion is to take the simple concepts developed for motion in one dimension and extend them to more complicated situations where motion has more than one degree of freedom, such as turning a car or the flight of a mosquito in three dimensions.
How does the lecture explain the calculation of the distance traveled by a car moving along a curved path?
-The lecture explains the calculation of the distance traveled by a car moving along a curved path by using the principles of calculus. It suggests breaking up the path into small straight-line segments, approximating the distance for each segment, and then summing these approximations to get the total distance traveled. This summation is represented mathematically as an integral of the speed function over the time interval of the journey.
What is the role of the Pythagorean theorem in the lecture?
-The Pythagorean theorem plays a crucial role in the lecture as it is used to calculate the magnitude of the velocity in two dimensions, which is necessary for determining the speed of an object moving in a plane. The theorem is applied to find the diagonal length of a right triangle formed by the horizontal and vertical components of velocity.
How does the lecture provide a proof for the Pythagorean theorem?
-The lecture provides a proof for the Pythagorean theorem by assembling four copies of a right triangle into a square. It shows that the area of the square formed by the hypotenuse of the right triangle is equal to the sum of the areas of the squares formed by the other two sides of the triangle. This visual proof demonstrates the relationship between the sides of a right triangle.
Outlines
🚗 Introduction to Complex Motion in Calculus
The video begins by highlighting the complexity of motion, explaining that objects like cars and mosquitoes do not move in straight lines but in various paths, including three-dimensional space. The instructor emphasizes that calculus starts with simple concepts, such as a car moving in a straight line, and then extends these to more complex scenarios. The goal is to analyze motion with more than one degree of freedom, asking questions about an object's position, velocity, and distance traveled over time. The video sets the stage for exploring instantaneous velocity and the total distance of non-linear paths using calculus.
📚 Vector-Valued Functions and Calculating Motion
This paragraph delves into the concept of vector-valued functions, using the example of a baseball's trajectory to illustrate how calculus can analyze motion in two dimensions. The baseball's x and y coordinates are given as functions of time, representing horizontal and vertical movements, respectively. The instructor explains how to calculate the ball's velocity in both directions and then combines these to find the overall velocity at any given time using the Pythagorean theorem. The discussion serves to connect the previous lecture's content with the current topic of complex motion analysis.
📉 Analyzing a Car's Path and Velocity
The script continues with a detailed example of a car moving along a plane, described by specific functions for its x and y coordinates over time. The car's path is analyzed by calculating its velocity at various points, obtained by taking the derivatives of its position functions. The horizontal and vertical velocities are then used to determine the car's speed at any time using the Pythagorean theorem. The paragraph also discusses the car's position at specific times, providing a visual understanding of its trajectory and the mathematical principles behind calculating its velocity.
🔍 Calculating Distance Traveled Using Integrals
This section introduces the problem of calculating the distance a car has traveled along a curved path over a given time interval. The instructor outlines the strategy of using calculus to break the path into small straight-line segments, approximating the distance traveled in each segment, and then summing these to find the total distance. The concept of an integral is introduced as the limit of this summation process as the time intervals become infinitesimally small. The paragraph concludes with the integral formula for finding the total distance traveled, emphasizing the integral's role in summing the small straight-line approximations.
📚 Practical Application: Calculating Distance with Calculus
The script provides a practical example of calculating the distance traveled by a car, using the previously introduced integral formula. The car's velocity function is derived from its position functions, and the integral of this velocity function over a specific time interval is computed. The fundamental theorem of calculus is applied to find the antiderivative of the velocity function, which is then evaluated at the bounds of the time interval to determine the total distance traveled. The example demonstrates the complete process of using calculus to solve a real-world problem of motion.
📐 Proof of the Pythagorean Theorem and Conclusion
The final paragraph of the script addresses a foundational mathematical principle used throughout the video—the Pythagorean theorem. The instructor presents an elegant geometric proof involving the assembly of four identical right triangles into a square, demonstrating the theorem's validity. An additional proof by the Indian mathematician Bhaskara is also briefly mentioned, highlighting the universality of mathematical knowledge across cultures and time. The video concludes with a look forward to the next lecture, where calculus will be extended to analyze different types of terrains.
Mindmap
Keywords
💡Motion
💡Derivative
💡Integral
💡Instantaneous Velocity
💡Vector Valued Function
💡Spatial Dimensions
💡Elliptical Orbit
💡Velocity
💡Pythagorean Theorem
💡Fundamental Theorem of Calculus
Highlights
Introduction to the concept of motion beyond straight lines, including cars and mosquitoes moving in three-dimensional space.
The development of calculus concepts starting with simple settings like a car moving in a straight line and extending to more complex scenarios.
Discussion on the types of questions that can be asked about motion, such as position, direction, and speed.
Explanation of how to determine the position of a moving object using spatial coordinates and time.
The concept of velocity as a combination of direction and speed, and its calculation using derivatives.
Instantaneous velocity and how it relates to the motion of a car not traveling on a straight line.
Use of calculus to analyze the distance traveled by a car on a curved path.
The baseball example to illustrate the concept of vector-valued functions in motion.
Calculation of the baseball's velocity components in both horizontal and vertical directions.
Geometric interpretation of velocity using the Pythagorean theorem to find the speed of the baseball.
Analysis of a car's motion along a specific path to determine the distance traveled using calculus.
Derivation of the car's velocity by taking the derivative of its position in both horizontal and vertical components.
Calculation of the car's speed at various times using the Pythagorean theorem.
Application of the fundamental theorem of calculus to find the total distance traveled by the car.
Proof of the Pythagorean theorem using geometric assembly of right triangles into a square.
An alternative proof of the Pythagorean theorem by Bhaskara, an Indian mathematician from the 12th century.
The significance of the Pythagorean theorem in resolving velocities into a single velocity vector.
The practical application of calculus in determining the distance traveled by a car on a curved path.
Transcripts
Browse More Related Video

Lecture 04: The Fundamental Theorem of Calculus

Motion problems with integrals: displacement vs. distance | AP Calculus AB | Khan Academy

Introduction to definite integrals
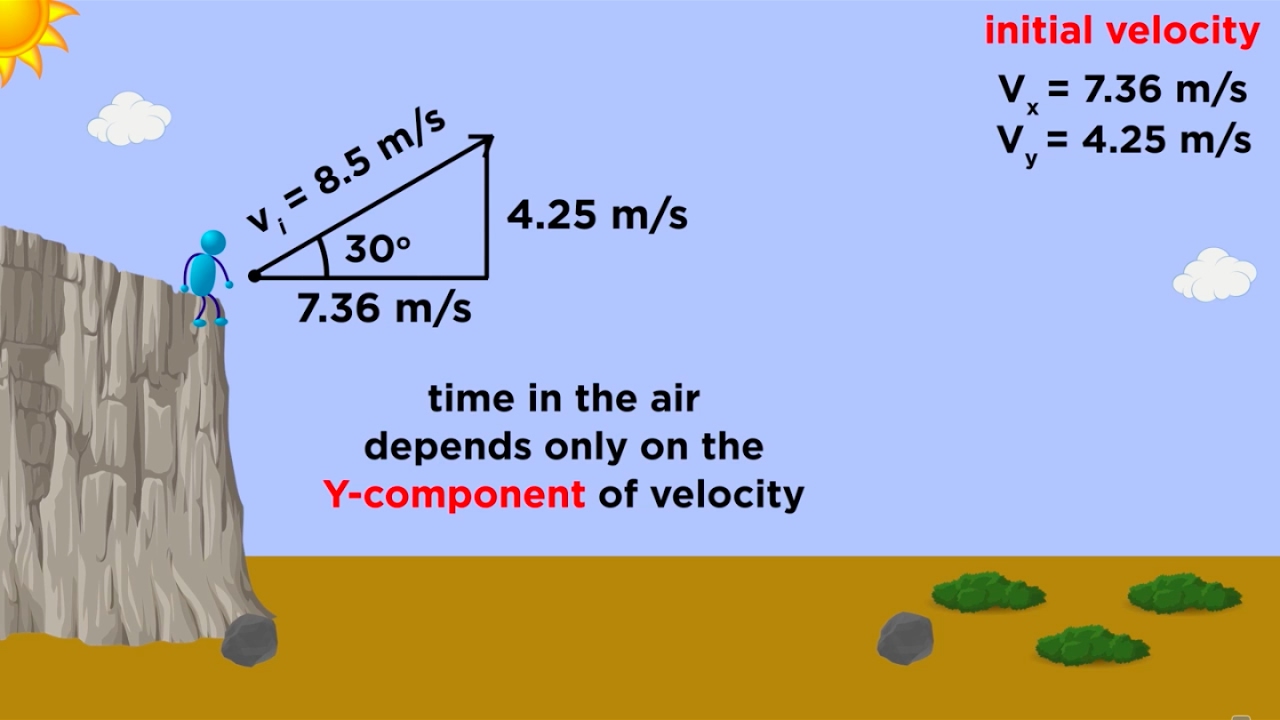
Kinematics Part 3: Projectile Motion

Lecture 10: The Integral and the Fundamental Theorem

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
5.0 / 5 (0 votes)
Thanks for rating: