Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
TLDRThe video script explores the concept of integrals as the inverse of derivatives, using the analogy of a car's velocity and distance traveled. It explains how integrals can be visualized as the area under a curve, which helps in understanding the relationship between velocity and distance. The script delves into approximating the distance traveled by summing areas of rectangles, leading to the fundamental theorem of calculus. It emphasizes the power of antiderivatives in calculating integrals and the significance of signed area in representing distance, including when the car moves backward.
Takeaways
- 🌟 Grothendieck's philosophy emphasizes the importance of understanding mathematical concepts intuitively before delving into formal proofs.
- 📈 The video focuses on the concept of integrals as the inverse operation of derivatives, using the analogy of a car's velocity and distance traveled.
- 🚗 The example of a car's changing velocity over time is used to illustrate how integrals can help determine the distance traveled without direct distance measurements.
- 📊 The concept of approximating the car's velocity as constant over small intervals and summing these to estimate the total distance is introduced.
- 🔄 The process of refining approximations by decreasing the time intervals (dt) leads to a better understanding of the actual distance traveled.
- 🏢 The area under the velocity-time graph represents the total distance traveled, which can be found by integrating the velocity function.
- 🔢 The antiderivative of a function is found by determining what function's derivative matches the original function, allowing the calculation of integrals.
- 🎢 The fundamental theorem of calculus is introduced, stating that the integral of a function is the antiderivative evaluated at the upper bound minus the lower bound.
- 🔄 The concept of 'negative area' is explained, where the integral can account for distances traveled in the opposite direction (e.g., when a car moves backward).
- 🌐 The video highlights the broad applicability of understanding integrals and the area under curves as a problem-solving tool in various scientific contexts.
- 🤝 The Art of Problem Solving is acknowledged as a sponsor, promoting creative math learning and exploration beyond traditional education methods.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is the relationship between integrals and derivatives, and how integrals can be thought of as the inverse operation of derivatives. The video uses the example of calculating distance traveled by a car based on its velocity function to illustrate this concept.
Why is it important to step back and make sure a mathematical fact feels reasonable and obvious?
-It is important because having an intuitive understanding of mathematical concepts helps build a deeper connection with the subject matter, making it easier to apply those concepts in various contexts and solve problems more effectively.
How does the video relate integrals to the area bounded by a velocity graph?
-The video relates integrals to the area bounded by a velocity graph by showing that the process of summing up small rectangles under the graph, each representing a small time interval, approximates the total distance traveled by the car. The limit of this sum as the time intervals become infinitesimally small gives the exact area under the curve, which represents the total distance.
What is the significance of the fundamental theorem of calculus mentioned in the video?
-The fundamental theorem of calculus is significant because it connects differentiation and integration, the two main operations in calculus. It states that if you know the derivative of a function, you can find the original function (antiderivative) that would produce the given derivative. This is crucial for solving many problems in mathematics and physics.
How does the process of refining the approximation of the car's motion by using smaller time intervals (dt) help in finding the distance traveled?
-Refining the approximation by using smaller time intervals (dt) allows for a more accurate representation of the car's changing velocity. As dt approaches zero, the sum of the areas of the rectangles under the velocity graph approaches the exact area under the curve, which is the precise distance traveled by the car.
What is the role of the constant 'c' in the antiderivative function?
-The constant 'c' in the antiderivative function accounts for the fact that there are infinitely many antiderivatives that can produce the same derivative. Adding or subtracting any constant 'c' from an antiderivative does not change its derivative, so the constant is added to match the specific initial conditions of a problem.
How does the video explain the concept of negative area in the context of integrals?
-The video explains that if a velocity function is negative, indicating the car is moving backward, the area of the rectangles representing distance traveled would be negative as well. This is because the product of a negative velocity and a time interval would result in a negative distance traveled. In the context of integrals, the signed area between the graph and the horizontal axis is considered, where areas below the axis are negative.
What is the role of the赞助商 (sponsor) mentioned in the video?
-The sponsor, The Art of Problem Solving, is mentioned as a company that supports the creation of educational content in the video. The speaker recommends their books and courses for those interested in developing a deeper understanding and love for mathematics.
How does the video demonstrate the process of finding the antiderivative of the function v(t) = 8t - t^2?
-The video demonstrates the process by first expressing the function as 8t - t^2 and then identifying the antiderivative by using the power rule for derivatives. The antiderivative is found to be 4t^2 - (1/3)t^3, and since any constant can be added to the antiderivative without changing its derivative, the final form is 4t^2 - (1/3)t^3 + c, where c is an arbitrary constant.
What is the practical application of the concepts discussed in the video?
-The practical application is in calculating distances traveled by objects with varying speeds, as well as in solving a wide range of mathematical and scientific problems that can be modeled as the sum of many small contributions. The concepts also provide a foundation for understanding more advanced topics in calculus and mathematical analysis.
Outlines
📚 Intuition Behind Integrals and Distance Traveled
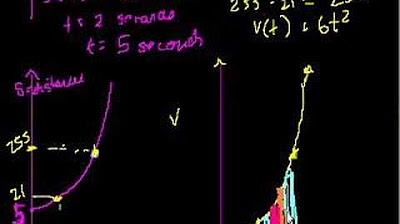
The paragraph introduces the concept of integrals as the inverse of derivatives, using the analogy of a car's distance traveled based on its velocity as observed from the speedometer. It explains how integrals can be visualized as the area under a curve, which represents the accumulation of small distances over time. The main idea is to build an intuitive understanding of integrals by relating them to the physical scenario of a car's motion, where the velocity function is known, and the goal is to find the corresponding distance function.
🔍 Approximating Distance with Constant Velocity Intervals
This paragraph delves into the method of approximating the distance traveled by treating the car's velocity as constant over small time intervals. It describes how the product of velocity and time (dt) for each interval can be visualized as the area of a rectangle, and by summing these areas, we approximate the total distance. The paragraph emphasizes the process of refining this approximation as the time intervals (dt) become smaller, ultimately leading to the precise calculation of distance by finding the area under the velocity curve.
📈 Deriving the Distance Function from Velocity
The focus of this paragraph is on deriving the distance function (s of t) from the given velocity function (v of t). It explains how the antiderivative of the velocity function gives us the distance function, with the caveat that an arbitrary constant can be added to the antiderivative without changing its derivative. The paragraph also introduces the concept of negative area, which occurs when the velocity is negative (the car moves backward), and how this is reflected in the signed area under the curve.
🌟 The Fundamental Theorem of Calculus
This paragraph highlights the Fundamental Theorem of Calculus, which connects the process of integration (finding the area under a curve) with the derivative of the antiderivative function. It emphasizes the elegance of calculus, where the integral of a function, representing the sum of infinitesimally small rectangles, can be computed by evaluating the antiderivative at just two points: the upper and lower bounds. The paragraph also touches on the concept of negative area and its significance in integral calculus.
🚀 Encouraging Exploration in Mathematics
The final paragraph steps away from the technical content to discuss the broader goal of the video series, which is to inspire viewers to explore mathematics on their own. It acknowledges the support from The Art of Problem Solving, a company that offers resources for developing a deep understanding and love for mathematics. The paragraph concludes by reiterating the success of the videos in motivating individuals to delve into the vast field of mathematics beyond the scope of the content presented.
Mindmap
Keywords
💡Grothendieck
💡Integrals
💡Derivatives
💡Antiderivatives
💡Signed Area
💡Velocity Graph
💡Fundamental Theorem of Calculus
💡Constant Velocity
💡Approximation
💡Area Under a Curve
💡The Art of Problem Solving
Highlights
The importance of understanding mathematical concepts intuitively, as suggested by Grothendieck's quote.
The introduction of integrals as the inverse operation of derivatives.
Using the example of a car's movement to explain the concept of integrals and distance functions.
The method of approximating velocity as constant over small time intervals to simplify calculations.
The visualization of distance traveled as the area under the velocity vs. time graph.
The process of refining approximations by decreasing the time interval (dt).
The explanation of integral notation and its representation of the limit of a sum as dt approaches 0.
The fundamental theorem of calculus, which connects derivatives and integrals.
The concept of antiderivatives and how they relate to the original function's integral.
The method of finding the antiderivative by identifying a function whose derivative matches the given function.
The impact of adding a constant to an antiderivative and how it affects the integral.
The practical application of the integral in calculating the distance traveled by a car with varying speed.
The explanation of negative area and its significance in integral calculus.
The general problem-solving tool of understanding and computing the area under a graph.
The discussion on the signed area measured by integrals when the function dips below the horizontal axis.
The sponsorship and recommendation of The Art of Problem Solving as a resource for creative math exploration.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: