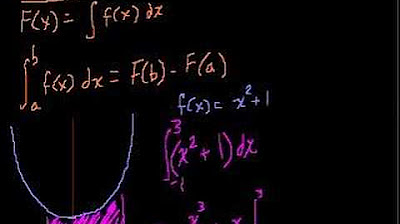Lecture 10: The Integral and the Fundamental Theorem
TLDRThis lecture delves into the concept of integrals, exploring their graphical and algebraic interpretations. Starting with the integral's definition, it uses the example of a car's velocity to illustrate how integrals can calculate distance traveled. The lecture progresses to explain the integral's graphical representation as the area under a curve and introduces the fundamental theorem of calculus, which links antiderivatives to integrals. It concludes by demonstrating how to find integrals algebraically by identifying antiderivatives and applying them to calculate areas under curves, showcasing the power of calculus in solving complex problems.
Takeaways
- 🚗 The concept of the integral was historically developed from calculating the distance traveled by a car based on its velocity over time.
- 📊 The integral can be interpreted graphically as the area under the curve of a function, which represents the accumulated value over a given interval.
- ➗ The integral notation, introduced by Leibniz, signifies summation (from the German word 'Summa') and involves the product of the function's value and the width of the interval (dt).
- 🔢 For simple cases, like a constant velocity, the integral can be calculated directly by multiplying the velocity by the time, which corresponds to the area of a rectangle under the curve.
- 📈 The integral of a velocity function that varies with time can be approximated by breaking the time interval into smaller segments and summing the areas of rectangles formed by assuming constant velocity in each segment.
- 🔴 The integral can handle negative values, representing reverse movement or negative velocities, and the result is the signed distance traveled.
- 🔄 The integral from point a to c can be found by adding the integral from a to b and then b to c, reflecting the additive property of the integral.
- 📚 The Fundamental Theorem of Calculus links the integral to the derivative by stating that the integral of a function can be found by evaluating the antiderivative at the limits of integration.
- 🔍 An antiderivative is a function whose derivative is the original function. Finding an antiderivative simplifies the process of integration.
- 📉 The integral can also be seen as an accumulation function, where the integral of a velocity function over time gives the position function, and vice versa through differentiation.
- 📚 The process of integration can be simplified by using the antiderivative method, which involves finding a function that, when differentiated, yields the original function, and then applying the fundamental theorem of calculus.
Q & A
What is the integral used to represent in the context of the lecture?
-In the context of the lecture, the integral is used to represent the total distance traveled by a car, computed from its velocity at every moment, as well as the area under the curve of a function, which can be interpreted as the net distance traveled or accumulated over time.
How is the integral notation represented and what does it signify?
-The integral notation is represented by an elongated 'S', which is an innovation by Leibniz. It signifies summation, as the first letter of the German word 'Summa'. Inside the integral sign, there's a function (e.g., velocity v(t)) and a differential (dt), which together represent the product of the height (velocity) and width (time interval) of rectangles used to approximate the area under the curve.
What is the graphical interpretation of the integral?
-The graphical interpretation of the integral is the area under the curve of a function between two points on the horizontal axis. This area can represent the net distance traveled by an object when the function represents its velocity over time.
How does the integral relate to the concept of velocity and distance traveled?
-The integral relates to the concept of velocity and distance traveled by representing the total distance an object has moved over time when its velocity is known at every moment. It's computed by multiplying the velocity at each instant by a small time interval and summing these products, which corresponds to the area under the velocity curve.
What is the significance of the integral in understanding the net distance traveled by a car?
-The integral is significant in understanding the net distance traveled by a car because it accounts for both the forward and backward movements. Even if the car moves back and forth, the integral will give the total distance covered, which is the area under the velocity curve, considering both positive and negative values.
How does the lecture explain the relationship between the integral and the area of a triangle?
-The lecture explains that if the velocity function is a straight line with a constant rate of change, such as 2t, it forms a triangle when graphed. The area under this curve, which represents the distance traveled, can be calculated as the area of the triangle using the formula (base * height) / 2.
What is the fundamental theorem of calculus and how does it relate to the integral?
-The fundamental theorem of calculus states that if a function's integral (or area under the curve) is to be found, one can instead find a function whose derivative is the original function and then evaluate this new function at the limits of integration. The difference in the function values at these limits gives the integral's value.
What is an antiderivative and how is it used to find the integral of a function?
-An antiderivative is a function whose derivative is the original function for which the integral is sought. It is used to find the integral by evaluating the antiderivative at the upper and lower limits of integration and then subtracting the two values.
How does the lecture illustrate the concept of antiderivatives with the example of the function 2x?
-The lecture illustrates the concept of antiderivatives by showing that x squared is an antiderivative of 2x because the derivative of x squared is 2x. To find the integral of 2x between two points, one would evaluate x squared at those points and subtract the results.
What is the role of constants in antiderivatives and why are they important?
-Constants are important in antiderivatives because adding a constant to an antiderivative does not change its derivative. This is due to the fact that the derivative of a constant is zero, and thus any constant added to an antiderivative will still have the original function as its derivative.
Can you provide an example from the lecture on how to find the integral of a polynomial function?
-The lecture provides the example of finding the integral of x to the power of n. By using the formula x to the power of (n+1) divided by (n+1), one can find the antiderivative of x to the power of n. This formula is derived from the rules of differentiation and can be used to find the integral between any two points by evaluating the antiderivative at those points and subtracting.
Outlines
📚 Introduction to the Integral Concept
This paragraph introduces the concept of the integral, drawing a connection to the previous lectures on derivatives. The lecturer begins by recalling the integral's definition, which was conceptualized through the example of a car's velocity over time to determine the total distance traveled. The integral is then related to the area under a graph, specifically the area under a constant velocity function over time. The paragraph sets the stage for a deeper exploration into the graphical and algebraic interpretations of the integral.
📈 Graphical Interpretation of the Integral
The lecturer delves into the graphical interpretation of the integral, explaining it as the area under the curve of a velocity function over time. The process of approximating this area by breaking the time interval into smaller segments and summing the areas of rectangles formed by assuming constant velocity within each segment is described. The integral's notation is highlighted, with a focus on its origin from Leibniz's notation, which signifies summation and the product of height (velocity) and width (time interval). The paragraph also touches on alternative methods to calculate the area under a curve, such as recognizing a straight line as a triangle and using geometric formulas to find its area.
🔍 Properties and Observations of the Integral
In this paragraph, the lecturer discusses the properties of the integral, particularly how it can be used to compute the net distance traveled by a car, even when the car is moving in reverse. The concept of the integral being additive is introduced, meaning the integral from point A to C can be found by adding the integral from A to B and from B to C. The paragraph also addresses the scenario where the function's value is negative, explaining that the integral will yield a negative area, reflecting the car's movement in the opposite direction. The importance of the integral in determining the final position after a journey, regardless of the direction of movement, is emphasized.
🚗 Accumulation of Distance and Position Function
The lecturer transitions to discussing the integral as an accumulation of distance traveled over time, introducing the concept of a position function. By integrating a velocity function, one can determine the position of an object at any given time, with the integral representing the net distance traveled. This paragraph explores how the integral's value changes in response to the velocity function's behavior, such as increasing when the velocity is positive and decreasing when the velocity is negative. The relationship between the velocity function and the position function is highlighted, with the integral of the velocity function equating to the position function.
📘 Fundamental Theorem of Calculus and Antiderivatives
This paragraph introduces the fundamental theorem of calculus, which links the concepts of derivatives and integrals. The lecturer explains that if a position function can be found whose derivative is the given velocity function, then the integral can be calculated by finding the difference between the position function's values at two points. The idea of antiderivatives is introduced as functions whose derivatives are equal to the original function. The paragraph provides examples of antiderivatives for certain functions and emphasizes the importance of the constant of integration, which arises because the derivative of a constant is zero.
🔢 Algebraic Manifestation of Integrals and Antiderivative Chart
The final paragraph focuses on the algebraic aspect of integrals, specifically the process of finding antiderivatives for various functions. The lecturer explains how to construct an antiderivative chart by reversing the process of differentiation. Examples are given to illustrate how to find antiderivatives for polynomial functions and trigonometric functions, and the importance of adding a constant to the antiderivative to account for the constant of integration is reiterated. The paragraph concludes by demonstrating how to use the antiderivative to calculate the integral of a function over a given interval, providing a method for students to compute integrals efficiently.
Mindmap
Keywords
💡Integral
💡Derivative
💡Graph
💡Area Under the Curve
💡Velocity Function
💡Antiderivative
💡Fundamental Theorem of Calculus
💡Position Function
💡Algebraic Interpretation
💡Limit of Integration
Highlights
Introduction to a series of lectures on integrals, following the exploration of derivatives.
Integral's definition and its relation to the distance traveled by a car with varying velocity.
Graphical interpretation of the integral as the area under a curve.
Algebraic interpretation of the integral involving the velocity function and time.
Explanation of how to calculate distance traveled with constant velocity using integral notation.
Visual representation of the integral as the area under a constant velocity function graph.
Strategy for calculating distance traveled with a velocity function that changes over time.
Fundamental definite integral as the sum of areas of rectangles approximating the area under the curve.
Introduction of Leibniz's notation for integrals and its significance.
Graphical correspondence of the integral as the area under a velocity curve.
Understanding the integral as an accumulation of distance over time.
Fundamental Theorem of Calculus linking the integral to the derivative.
Deriving position functions from velocity functions using integration.
Graphical representation of the integral showing how velocity affects position.
Algebraic method for finding the integral of a function using antiderivatives.
Explanation of how to find the integral of x^n using the power rule for antiderivatives.
Understanding that adding a constant to an antiderivative does not change its derivative.
Practical application of antiderivatives to calculate areas under curves.
Summary of the graphical and algebraic manifestations of integrals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: