Introduction to definite integrals
TLDRThe video script presents a clear and illustrative discussion on the application of antiderivatives in calculating the area under a curve, using the context of physics to explain the concept. It introduces the relationship between distance and velocity, demonstrating how derivatives and antiderivatives can be used to determine an object's instantaneous velocity and the total distance traveled over time. The explanation is complemented with a visual representation of the concepts, enhancing the viewer's understanding of the fundamental principles of calculus as they relate to real-world motion.
Takeaways
- 📈 The presentation focuses on using antiderivatives to calculate the area under a curve, which has applications in physics.
- 🌟 The concept is introduced with an example from physics, relating distance (s) and velocity (v) over time (t).
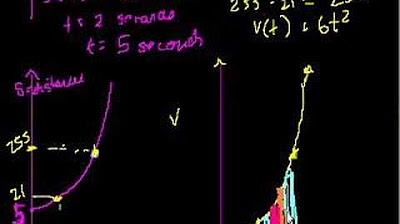
- 🛤️ The position of a moving object is described by the formula s = 16t^2, where s represents distance and t represents time.
- 📊 A graph of the position function results in a parabolic curve, illustrating the object's accelerating motion.
- 🏃 The velocity of the object is the derivative of the distance function with respect to time, calculated as v = ds/dt = 32t.
- 📈 The graph of velocity over time is a straight line with a slope of 32, representing the instantaneous velocity at any given time.
- 🔄 The relationship between distance and velocity is highlighted: the derivative of distance gives velocity, and the antiderivative of velocity gives distance.
- 🕒 For a constant velocity, the distance traveled can be calculated as the product of velocity and time.
- 🔺 The concept of 'infinitesimal' time intervals (delta t or dt) is introduced to approximate the distance traveled by summing the areas of skinny rectangles.
- 📝 The process of summing the areas of these rectangles refines the approximation of the total distance traveled over time.
- 🎯 As the width of the rectangles approaches zero (becoming infinitesimally small), the sum of their areas converges to the exact area under the curve, which is the total distance traveled.
Q & A
What is the main topic of the presentation?
-The main topic of the presentation is the use of antiderivatives to calculate the area under a curve, with a focus on the intuition behind the concept.
How does the presenter relate the concept of antiderivatives to physics?
-The presenter uses the example of distance and velocity from physics to illustrate how derivatives and antiderivatives can be applied in real-world scenarios.
What is the position function given in the example?
-The position function given in the example is s = 16t^2, where s represents distance and t represents time.
Why does the presenter choose to graph the curve for positive t only?
-The presenter chooses to graph the curve for positive t only because, in the context of the lecture, it is not possible to go back in time, and the curve represents the position of an object at a given time.
What is the derivative of the distance function, and what does it represent?
-The derivative of the distance function is ds/dt = 32t, which represents the velocity of the object at any given time t.
How does the presenter describe the relationship between distance, velocity, and time?
-The presenter describes the relationship as follows: distance is the integral (antiderivative) of velocity, and velocity is the derivative of distance. In other words, the derivative of distance with respect to time gives us velocity, and the antiderivative of velocity with respect to time gives us distance.
What is the significance of the small time fragment (delta t or dt) in the explanation?
-The small time fragment (delta t or dt) is used to represent an infinitesimally small change in time. Over this small period, the velocity is considered roughly constant, allowing the presenter to calculate the distance traveled during this time interval as the product of the velocity and the change in time.
How does the presenter visualize the calculation of distance over time?
-The presenter visualizes the calculation by imagining the area under the velocity curve (or in this case, a straight line) as the total distance traveled. This is done by summing the areas of infinitesimally thin rectangles, each representing the distance traveled during a small time interval.
What happens as the size of the time intervals (dt's) becomes smaller in the calculation?
-As the size of the time intervals (dt's) becomes smaller, the approximation of the total distance traveled becomes more accurate. This is because the rectangles used to approximate the area under the curve become thinner and more numerous, leading to a closer approximation of the actual area under the curve.
What is the main takeaway from the presentation regarding the use of calculus in physics?
-The main takeaway is that calculus, specifically derivatives and antiderivatives, can be used to solve physical problems involving rates of change, such as calculating the distance traveled by an object when given its velocity over time.
How does the presenter plan to continue the discussion in the next presentation?
-The presenter plans to continue the discussion in the next presentation by further exploring the concepts introduced and possibly covering additional applications of calculus in physics.
Outlines
📈 Introduction to Antiderivatives and Area Under a Curve
The paragraph begins with an introduction to the concept of antiderivatives and their application in calculating the area under a curve. The speaker uses an example from physics, specifically focusing on distance and velocity, to illustrate the relationship between derivatives and antiderivatives. The speaker introduces a position function, s(t) = 16t^2, to represent the distance traveled by an object over time, t, and explains how to graph this function as a parabola. The concept of acceleration is briefly discussed, and the speaker transitions to explaining how to find the velocity of the object by taking the derivative of the distance function with respect to time. The velocity function, v(t) = 32t, is then graphed as a straight line with a slope of 32. The paragraph concludes with the speaker emphasizing the connection between the derivative of distance (velocity) and the antiderivative of velocity (distance), while noting that the specific starting position of the object is not known.
🤔 Deriving Distance from Velocity and the Concept of Infinitesimal Time
In this paragraph, the speaker explores the reverse process of finding the distance traveled by an object when only the velocity function is known. The speaker introduces the concept of infinitesimal time, represented as delta t (dt), and explains how to use this to calculate the distance traveled over a very small time interval. By multiplying the constant velocity during this small time interval by the time itself, the speaker demonstrates that the result is the area of a thin rectangle, which represents the distance traveled. The speaker then describes a method for approximating the total distance traveled after a certain time, t sub nought, by summing the areas of these infinitesimally small rectangles. As the size of dt decreases, the approximation becomes more accurate, eventually converging to the exact area under the curve, which in this case is a line, representing the total distance traveled. The paragraph ends with the speaker noting the time constraints and indicating that the topic will be continued in the next presentation.
Mindmap
Keywords
💡antiderivative
💡intuition
💡position
💡velocity
💡derivative
💡distance
💡graph
💡time
💡area under a curve
💡integration
Highlights
The presentation focuses on using antiderivatives to calculate the area under a curve, providing an intuitive understanding.
A physics example is used to illustrate the concept, linking distance and velocity to make the topic relatable and easier to grasp.
The position of a moving object is described using the formula s = 16t^2, where s represents distance and t represents time.
The graph of the position function is a parabola, demonstrating the object's accelerating motion over time.
The velocity of the object is determined by taking the derivative of the distance function, showcasing the application of derivatives.
The derivative of the distance function with respect to time (ds/dt) is found to be 32t, representing the instantaneous velocity.
The graph of the velocity function is a straight line with a slope of 32, illustrating the constant rate of acceleration.
The relationship between the distance formula and its derivative is highlighted, where the derivative of distance gives velocity, and the antiderivative of velocity gives distance.
The concept of calculating distance traveled over time by summing the areas of infinitesimally small rectangles is introduced.
The method of approximating the area under a curve using smaller and smaller rectangles (dt's) is explained, leading to a more accurate representation of the total distance traveled.
The presentation suggests a future session dedicated to using calculus for physics, specifically focusing on the application of derivatives in this context.
The importance of understanding the relationship between distance and velocity, and how derivatives and antiderivatives play a role in this relationship, is emphasized.
The practical application of this mathematical concept is demonstrated, showing how it can be used to determine the distance an object has traveled after a certain amount of time.
The presentation concludes with a teaser for the next session, promising a continuation of the discussion on the application of calculus in physics.
Transcripts
Browse More Related Video

Definite integrals (part II)

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus

Average velocity for constant acceleration | One-dimensional motion | Physics | Khan Academy

Lecture 10: The Integral and the Fundamental Theorem

Area under rate function gives the net change | AP Calculus AB | Khan Academy
Definite Integrals (area under a curve) (part III)
5.0 / 5 (0 votes)
Thanks for rating: