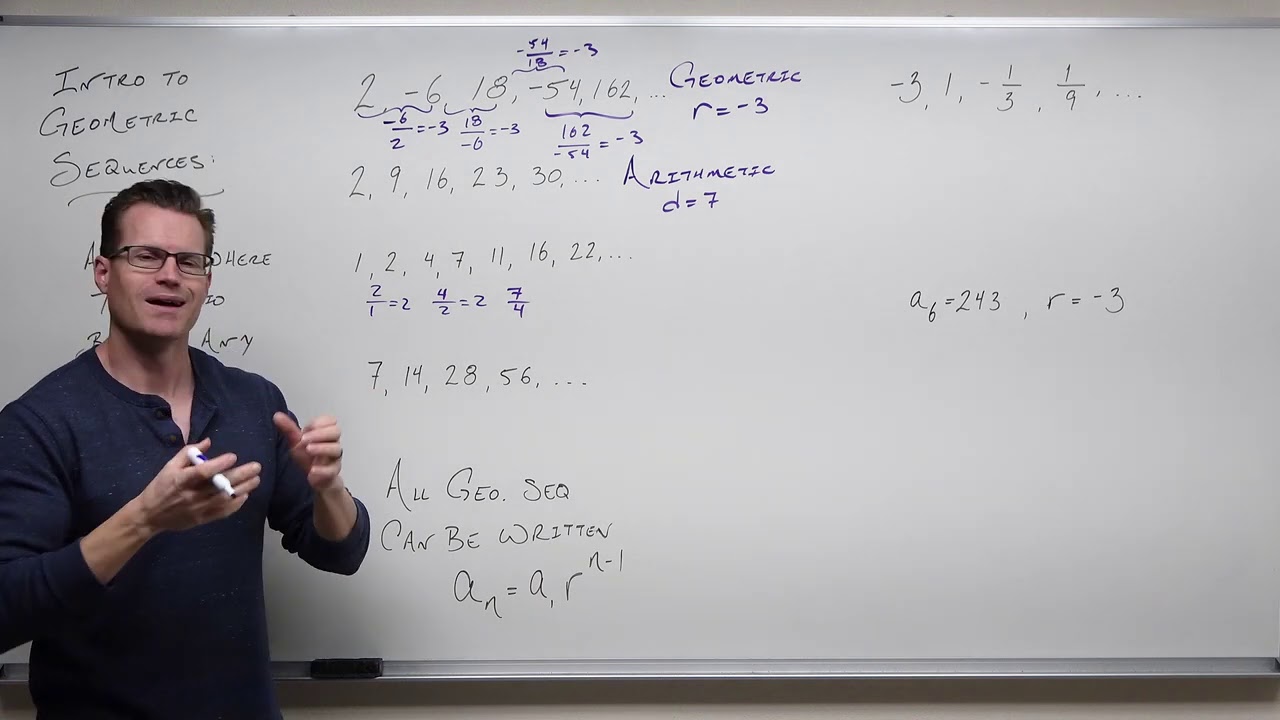ILLUSTRATING SEQUENCES AND SERIES || PRECALCULUS
TLDRThis educational video lesson delves into the concepts of sequences and series, illustrating the differences between the two. It defines a sequence as a function with a domain of positive integers, which can be either finite or infinite. The video provides examples of how to find the terms of a sequence given a general formula, such as a_n = n - 3^n. It then explains arithmetic sequences, where each term is found by adding a constant (common difference) to the previous one, and geometric sequences, where terms are found by multiplying the previous term by a constant (common ratio). The Fibonacci sequence is introduced as a special case where each term is the sum of the two preceding ones. The lesson also covers how to determine the type of sequence (arithmetic, geometric, or Fibonacci) given a set of numbers and how to calculate the sum of the first n terms of an arithmetic series. Practical applications, such as calculating savings over a period where the amount saved triples each day, are also discussed. The video concludes with an encouragement to like, subscribe, and stay updated for more informative content.
Takeaways
- 😀 A sequence is a function defined on the set of positive integers, representing an ordered list of numbers.
- 🔍 Infinite sequences continue indefinitely, while finite sequences have a last term, denoted by ellipses.
- 📝 Each number in a sequence is called a term, with the first term being the initial value in the sequence.
- 🔢 The general term of a sequence is given by a formula, which can be used to find any term in the sequence.
- ⚖️ An arithmetic sequence is characterized by a common difference between consecutive terms.
- 🔄 A geometric sequence has a common ratio, which is used to find subsequent terms by multiplying the previous term by this ratio.
- 🌐 The Fibonacci sequence is a special type of sequence where each term is the sum of the previous two terms.
- 📊 A series is the sum of the terms of a sequence, and it can be represented by a sigma notation.
- 💰 The script includes an example of a geometric sequence problem involving savings that triple each day, illustrating how to calculate the total savings.
- 📚 The lesson differentiates between arithmetic, geometric, and Fibonacci sequences, and explains how to identify and work with each type.
- 🎓 The video aims to educate viewers on the concepts of sequences and series, providing clear examples and exercises for understanding.
Q & A
What is a sequence in mathematical terms?
-A sequence is a function whose domain is the set of positive integers, essentially an ordered list of numbers that can be finite or infinite.
How is an infinite sequence represented?
-An infinite sequence is represented with an ellipsis (...) to show that it continues indefinitely without a last term.
What is the difference between a finite and an infinite sequence?
-A finite sequence has a last term and its domain is a set of positive integers up to a certain number 'n', while an infinite sequence continues indefinitely without an end.
What is the term used to describe each number in a sequence?
-Each number in a sequence is referred to as a term.
How do you find the first five terms of a sequence given by a general term formula?
-You substitute the values 1, 2, 3, 4, and 5 into the general term formula to find the first five terms of the sequence.
What is an arithmetic sequence?
-An arithmetic sequence is a sequence in which each term after the first is obtained by adding a constant number, called the common difference, to the preceding term.
What is the common difference in an arithmetic sequence?
-The common difference in an arithmetic sequence is the constant number added to each term to get the next term.
What is a geometric sequence?
-A geometric sequence is a sequence where each term after the first is obtained by multiplying the preceding term by a constant number, known as the common ratio.
What is the common ratio in a geometric sequence?
-The common ratio in a geometric sequence is the constant factor by which each term is multiplied to get the next term.
What is a Fibonacci sequence?
-A Fibonacci sequence is a series where each term is the sum of the two preceding terms, typically starting with 0 and 1 or 1 and 1.
What is the difference between a sequence and a series?
-A sequence is an ordered list of numbers, while a series is the sum of the terms of a sequence.
How do you calculate the sum of the first 'n' terms of an arithmetic series?
-The sum of the first 'n' terms of an arithmetic series can be calculated using the formula: S_n = n/2 * (first term + last term).
Can you provide an example of a geometric sequence and its common ratio?
-An example of a geometric sequence is 1, 3, 9, 27, 81 with a common ratio of 3, since each term is obtained by multiplying the previous term by 3.
What is the sum of the first six terms of the sequence 5, 15, 25, 35, and 45?
-The sum of the first six terms of the sequence would be 5 + 15 + 25 + 35 + 45, which equals 125.
How much money would you have saved after a week if you save 20 pesos on the first day, 60 pesos on the second day, and continue to triple your money each day for seven days?
-Following the pattern of a geometric sequence with a common ratio of 3, after a week, you would have saved 20 + 60 + 180 + 540 + 1620 + 4860 + 14580, which totals 21860 pesos.
Outlines
📚 Introduction to Sequences and Series
This paragraph introduces the concept of sequences and series in mathematics. It explains that a sequence is a function with a domain of positive integers, which can be finite or infinite. The paragraph illustrates the idea with examples, such as an ellipses representing an infinite sequence and a finite sequence defined up to a term 'n'. It also introduces the terms 'first term', 'second term', etc., and provides an example of finding the first five terms of a sequence given by a general formula. The explanation is geared towards differentiating series from sequences and setting the foundation for further mathematical discussions in the video.
🔢 Understanding Arithmetic and Geometric Sequences
The second paragraph delves into the specifics of arithmetic and geometric sequences. An arithmetic sequence is defined as one where each term after the first is obtained by adding a constant number, known as the common difference. Examples are given to illustrate this, such as the sequence 25, 23, 21, 19, 17, where the common difference is -2. Conversely, a geometric sequence is characterized by each term after the first being obtained by multiplying the preceding term by a constant number, the common ratio. The paragraph provides examples of both types of sequences and explains how to identify the common difference and common ratio. It also includes exercises for the viewer to apply these concepts.
🌐 Exploring the Fibonacci Sequence and Series
This paragraph introduces the Fibonacci sequence, which is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. The paragraph provides examples of Fibonacci sequences and explains how to identify and calculate subsequent terms. It also discusses the concept of a series, which is the sum of the terms of a sequence. The explanation includes how to represent series and sequences, and it provides examples of calculating the sum of the first few terms of both arithmetic and geometric sequences, as well as the Fibonacci sequence.
🧮 Summation of Arithmetic Series and Problem Solving
The fourth paragraph focuses on the summation of arithmetic series, providing a method to calculate the sum of the first few terms of an arithmetic sequence. It offers a detailed example of how to find the sum of the first four terms of a sequence and then generalizes the process for finding the sum of an arithmetic series. The paragraph also presents a problem-solving scenario where the viewer is asked to calculate the total savings over a week, given a geometric sequence of savings that triple each day. The solution involves summing the geometric sequence and arrives at a total savings amount.
💰 Practical Application of Geometric Sequences in Savings
The final paragraph applies the concept of geometric sequences to a real-world scenario of savings. It describes a situation where an individual saves a certain amount of money each day, with the amount saved tripling each subsequent day. The paragraph outlines the geometric sequence of savings for seven days and then calculates the total savings by summing up the daily amounts. The result is a significant total savings figure, demonstrating the power of compounding in geometric sequences. The paragraph concludes with a call to action for viewers to engage with the content by liking, subscribing, and turning on notifications for more video tutorials.
Mindmap
Keywords
💡Sequence
💡Series
💡Term
💡Arithmetic Sequence
💡Geometric Sequence
💡Fibonacci Sequence
💡Common Difference
💡Common Ratio
💡Sum of a Series
💡Problem Solving
Highlights
A sequence is a function whose domain is the set of positive integers, representing an ordered list of numbers.
An infinite sequence has a domain of positive integers without a last term, denoted by ellipses.
A finite sequence has a domain of positive integers up to a certain term 'n', with a last term.
Each number in a sequence is called a term, with specific terms like first term, second term, etc.
The general term of a sequence is given by a formula, such as a_n = n - 3^n.
Arithmetic sequences are defined by adding a constant number, called the common difference, to the preceding term.
Geometric sequences are formed by multiplying a constant number, the common ratio, to the preceding term.
The Fibonacci sequence is a special type of sequence where each term is the sum of the previous two terms.
A series is the sum of the terms of a sequence, represented by a sigma (Σ) notation.
The sum of the first n terms of an arithmetic series can be calculated using the formula S_n = n/2 * (a_1 + a_n).
To find the sum of a geometric series, each term is multiplied by the common ratio raised to the power of the term's position.
The first five terms of a sequence can be determined using the general term formula and substituting values for n.
A sequence can be identified as arithmetic, geometric, or Fibonacci based on the relationship between consecutive terms.
The sum of an arithmetic series can be found by adding the first and last terms, then multiplying by the number of terms divided by 2.
A geometric series can be represented as a fraction with the first term, common ratio, and the term raised to the power of the number of terms minus 1 in the denominator.
In a practical application, a geometric sequence can model the growth of savings when money is tripled each day.
The sum of a geometric sequence can be calculated by adding all the terms from the first to the last day.
The video provides a step-by-step guide to understanding and working with sequences and series, including examples and exercises.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: