Ch. 12.3 Geometric Sequences

Prof. Williams
6 May 202211:38
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture introduces geometric sequences, a type of sequence where each term is a constant multiple of the previous one, denoted by 'r'. It contrasts geometric sequences with arithmetic sequences and illustrates the concept with an example, explaining how to find 'a' and 'r'. The instructor then derives the formula for the nth term and the nth partial sum of a geometric sequence. An example is provided to calculate the sum of the first ten terms. The video also explores infinite series, explaining the concept of convergence and divergence, with a specific focus on when the series converges if the common ratio 'r' is less than one.

Takeaways
  • 📚 The lecture introduces Chapter 12.3 on geometric sequences, the last type of sequence to be discussed before exploring their applications.
  • 🔢 Geometric sequences are characterized by a constant ratio 'r' between consecutive terms, starting with a constant 'a', unlike arithmetic sequences which have a constant difference.
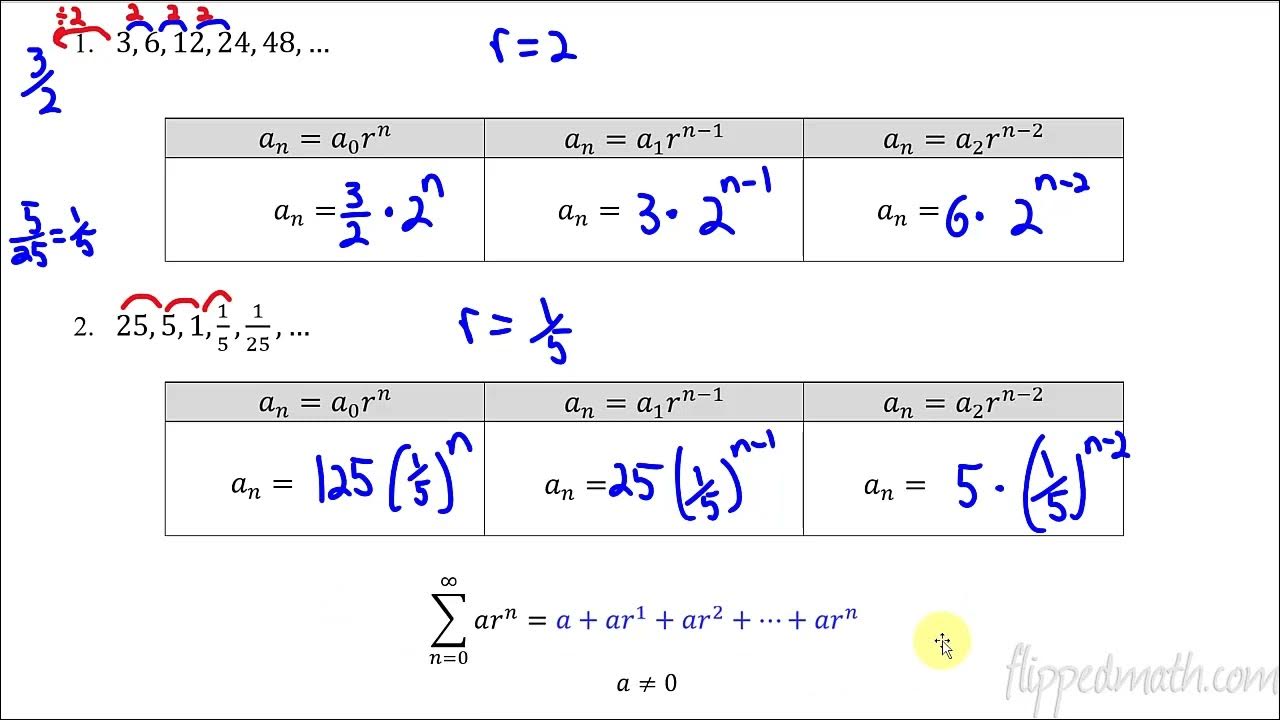
  • 🌱 An example of a geometric sequence is given as 3, 6, 12, 24, etc., where each term is the previous term multiplied by 2.
  • 🔑 To find the first term 'a' of a geometric sequence, it is simply the first value in the sequence. The common ratio 'r' can be found by dividing any term by the previous one.
  • 🧩 The general term of a geometric sequence is given by the formula a * r^(n-1), where 'n' is the term number.
  • 📊 The nth partial sum of a geometric sequence can be calculated using the formula a * (1 - r^n) / (1 - r), which is derived through a series manipulation technique.
  • 🔍 An example calculation is provided to find the sum of the first 10 terms of a geometric sequence with a = 3 and r = 2/3, resulting in a precise fraction.
  • ♾ The concept of infinite series is introduced, discussing the sum of a sequence that continues indefinitely.
  • 🔄 The sum of an infinite geometric series converges to a finite value if the common ratio 'r' is less than 1, otherwise, it diverges to infinity or negative infinity.
  • 📐 A visual representation of the convergence of an infinite series is given using the example of adding up areas of squares with decreasing side lengths.
  • 📘 The formula for the sum of an infinite geometric series is S = a / (1 - r), applicable when |r| < 1, indicating the series converges to a specific value.
Q & A

  • What is the main topic of Chapter 12.3 in the transcript?

    -The main topic of Chapter 12.3 is geometric sequences.

  • What is the defining characteristic of a geometric sequence?

    -A geometric sequence is defined by the fact that each term after the first is found by multiplying the previous one by a constant called the common ratio (r).

  • How does the growth in a geometric sequence differ from an arithmetic sequence?

    -In a geometric sequence, the growth is exponential as each term is a multiple of the previous term, whereas in an arithmetic sequence, the growth is linear with a constant difference between terms.

  • What is the general form of the nth term of a geometric sequence?

    -The general form of the nth term of a geometric sequence is a * r^(n-1), where 'a' is the first term and 'r' is the common ratio.

  • How can you find the common ratio (r) of a geometric sequence if you have two consecutive terms?

    -You can find the common ratio (r) by dividing any term by the previous term, i.e., r = term_n / term_(n-1).

  • What is the formula for finding the nth partial sum of a geometric sequence?

    -The formula for the nth partial sum (S_n) of a geometric sequence is a * (1 - r^n) / (1 - r), where 'a' is the first term and 'r' is the common ratio, provided that r is not equal to 1.

  • What is an example of a geometric sequence given in the transcript?

    -An example of a geometric sequence given in the transcript is 3, 2, 4/3, 8/9, etc., with a common ratio of 2/3.

  • What is the difference between a convergent and a divergent series?

    -A convergent series is one that approaches a single value as the number of terms goes to infinity, while a divergent series does not approach a single value and tends towards infinity or negative infinity.

  • What is the sum of an infinite geometric series if the common ratio (r) is less than one?

    -If the common ratio (r) is less than one, the sum of an infinite geometric series converges to the value a / (1 - r), where 'a' is the first term.

  • How can you determine if a geometric series is convergent or divergent?

    -A geometric series is convergent if the common ratio (r) is less than 1 and divergent if r is equal to or greater than 1.

  • What is the sum of the geometric series 1 + 1/2 + 1/4 + ... if it is convergent?

    -The sum of the convergent geometric series 1 + 1/2 + 1/4 + ... is 2, as each term represents half the area of the previous rectangle in a geometric progression of areas.

Outlines
00:00
📚 Introduction to Geometric Sequences

In this section, the instructor introduces geometric sequences, explaining that they are the last type of sequence to be discussed. A geometric sequence starts with a constant 'a' and each subsequent term is multiplied by a constant ratio 'r'. This differs from arithmetic sequences, which have a constant difference between terms. An example sequence is provided: starting with 3, each term is multiplied by 2, resulting in 3, 6, 12, 24, etc. The instructor highlights the rapid growth of geometric sequences compared to arithmetic ones.

05:02
🔍 Finding the Common Ratio in Geometric Sequences

The instructor explains how to identify the common ratio 'r' in a geometric sequence by using an example sequence: 3, 2, 4/3, 8/9, etc. The first term 'a' is given as 3, and to find 'r', the instructor sets up an equation using two consecutive terms. By solving 3r = 2, they find r = 2/3. The general term of the sequence is then expressed as 3 * (2/3)^(n-1). The instructor also discusses how to calculate the nth partial sum of the sequence by multiplying and subtracting terms to simplify the formula.

10:04
📈 Calculating the Nth Partial Sum of a Geometric Sequence

The instructor demonstrates the calculation of the nth partial sum of a geometric sequence, using the previously discussed sequence (a = 3, r = 2/3). By plugging the values into the formula for the nth partial sum, they show the detailed steps to find the sum of the first 10 terms. The process includes algebraic manipulations to handle fractions and ensure accuracy. The final exact value is obtained, emphasizing the importance of precision in these calculations.

♾️ Understanding Infinite Geometric Series

This section explores the concept of infinite geometric series. The instructor addresses the intuition that summing an infinite number of terms would lead to infinity but explains that certain series can converge to a finite value. Using the sequence 1, 1/2, 1/4, 1/8, etc., with a common ratio of 1/2, the instructor illustrates how the sum of these terms approaches 2 as more terms are added. The convergence criterion is stated: if the absolute value of r is less than 1, the series converges to a/(1-r). For r >= 1, the series diverges.

Mindmap
Keywords
💡Geometric Sequence
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. In the video, the geometric sequence is introduced as the last type of sequence to be discussed, and the concept is exemplified by a sequence starting with 3 and each subsequent term being multiplied by 2, thus illustrating the rapid growth characteristic of geometric sequences.
💡Common Ratio (r)
The common ratio, denoted as 'r', is the factor by which each term in a geometric sequence is multiplied to get the next term. In the script, the common ratio is used to determine the pattern of the sequence, with the example given where each term is twice the previous one, hence r equals 2.
💡Arithmetic Sequence
Although not the main focus of the video, an arithmetic sequence is contrasted with a geometric sequence. In an arithmetic sequence, each term is found by adding a constant difference to the previous term, unlike the multiplicative relationship in a geometric sequence. The script mentions this to highlight the difference in growth patterns between arithmetic and geometric sequences.
💡General Term
The general term of a sequence refers to the nth term in the sequence, which can be expressed with a formula. In the context of the video, the general term of a geometric sequence is given by the formula 'a * r^(n-1)', where 'a' is the first term and 'r' is the common ratio, as demonstrated with the sequence starting with 3 and having a common ratio of 2/3.
💡Partial Sum
The partial sum of a sequence is the sum of the first n terms of that sequence. The script explains how to calculate the nth partial sum of a geometric sequence using a formula, which involves the first term 'a', the common ratio 'r', and the term number 'n', and is crucial for understanding the accumulation of sequence values.
💡Infinite Series
An infinite series is the sum of an infinite number of terms in a sequence. The video discusses the concept of summing a geometric sequence without an upper limit, which can either converge to a finite value or diverge to infinity, depending on the common ratio.
💡Convergent Series
A convergent series is one where the sum of its terms approaches a single value as more terms are added. The script explains that a geometric series with a common ratio less than one will converge, using the example of a series with a common ratio of 1/2 that converges to a sum of 2.
💡Divergent Series
A divergent series is one where the sum of its terms does not approach a finite value but instead heads towards infinity or negative infinity. The video mentions that if the common ratio 'r' is equal to or greater than 1, the series will diverge.
💡First Term (a)
The first term of a sequence, denoted as 'a', is the starting point of the sequence. In the script, the first term is identified as the base value from which subsequent terms in a geometric sequence are derived by multiplication with the common ratio.
💡nth Partial Sum Formula
The nth partial sum formula is a mathematical formula used to calculate the sum of the first n terms of a geometric sequence. The script derives this formula through a process of manipulation involving multiplying the partial sum by the common ratio 'r' and then subtracting this from the original partial sum to isolate the nth term.
💡Geometric Series Representation
The geometric series representation refers to the way an infinite geometric series can be visualized and summed. In the video, this is illustrated by adding areas of squares and rectangles to represent the terms of the series, showing how the sum approaches a certain value without ever exceeding it.
Highlights

Introduction to geometric sequences as the last type of sequence to be discussed in the section.

Explanation of geometric sequence formation starting with a constant 'a' and each term multiplied by a constant 'r'.

Comparison between geometric and arithmetic sequences in terms of growth rate and progression.

Example of a geometric sequence starting with 3 and each term multiplied by 2.

Method to identify the constant 'a' in a given sequence.

Process to find the common ratio 'r' using consecutive terms of a geometric sequence.

General term formula for a geometric sequence expressed as 'a * r^(n-1)'.

Technique to calculate the nth partial sum of a geometric sequence.

Derivation of the formula for the nth partial sum involving subtraction and simplification.

Final formula for the nth partial sum: 'a * (1 - r^n) / (1 - r)'.

Example calculation of the sum of the first 10 terms of a geometric sequence with 'a' as 3 and 'r' as two-thirds.

Discussion on the sum of an infinite geometric series and its conditions for convergence.

Illustration of a geometric series with squares to demonstrate the concept of convergence.

Criteria for a geometric series to be convergent: 'r' must be less than 1.

Formula for the sum of an infinite geometric series: 'a / (1 - r)'.

Explanation of divergent series and their behavior towards positive or negative infinity.

Mention of the possibility of a series alternating and oscillating without converging or diverging.

Transcripts

Browse More Related Video

Geometric Series (Precalculus - College Algebra 72)

Calculus BC – 10.2 Working with Geometric Series

ILLUSTRATING SEQUENCES AND SERIES || PRECALCULUS

Geometric Sequences (Precalculus - College Algebra 71)

Ch. 12.2 Arithmetic Sequences

Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsEducationSequencesGeometricSeriesCalculusInfinite SeriesArithmeticAlgebraProblem SolvingEducational Content