Three Types of Discontinuities in Functions

turksvids
29 Feb 202014:18
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the three main types of discontinuities in functions: removable, jump, and infinite discontinuities. Removable discontinuities, often visualized as holes in the graph, occur when the limit exists and is finite but not equal to the function's value at that point. Jump discontinuities are characterized by the function's left and right limits being different constants, creating a 'jump' between them. Infinite discontinuities, synonymous with vertical asymptotes, happen when the function's limit approaches infinity as it approaches a certain point. The script provides algebraic examples and emphasizes the importance of understanding limits in identifying these discontinuities, which is crucial for AP Calculus students.

Takeaways
  • 📊 There are three types of discontinuities in functions: removable, jump, and infinite discontinuities.
  • 🕳️ Removable discontinuities, also known as holes, occur when the limit exists and is finite but not equal to the function's value at that point.
  • 🔢 For a removable discontinuity, the function's value at the point may not exist, or it could be different from the limit as x approaches that point.
  • ⏏️ Infinite discontinuities, or vertical asymptotes, happen when the function's value approaches infinity or negative infinity as x approaches a certain point.
  • 🚫 A jump discontinuity is characterized by the left and right limits approaching different finite values, resulting in a 'jump' in the graph.
  • 🔍 To identify discontinuities, look for factors in the denominator that do not cancel out with factors in the numerator.
  • 📉 A function with a removable discontinuity can be simplified by canceling out common factors, revealing the discontinuity.
  • 🔁 For jump discontinuities, evaluate the left and right limits separately to determine if they are equal; if not, a jump exists.
  • 📍 The absolute value function, f(x) = |x|/x, is a classic example of a function with a jump discontinuity at x = 0.
  • ∞ When dealing with infinite discontinuities, look for one-sided limits (from the left or right) that approach positive or negative infinity.
  • 📌 Even piecewise functions can have discontinuities, and it's important to evaluate the limits from the left and right at the points of transition.
Q & A

  • What are the three types of discontinuities in functions?

    -The three types of discontinuities in functions are removable, jump, and infinite discontinuities.

  • How are removable discontinuities represented on a graph?

    -Removable discontinuities are represented as holes in the graph, where the function approaches the same point from the left and right but does not exist at that point.

  • What are the conditions for a function to have a removable discontinuity?

    -A function has a removable discontinuity if the limit as X approaches C of f(X) exists and is finite, the limit from the left equals the limit from the right, and f(C) is not equal to the limit as X approaches C of f(X).

  • How is a jump discontinuity graphically represented?

    -A jump discontinuity is graphically represented by a sudden 'jump' from one value to another without reaching the intermediate values, appearing as a gap in the graph.

  • What is the condition for a function to have a jump discontinuity?

    -A function has a jump discontinuity if the limit as X approaches C from the left of f(X) is not equal to the limit as X approaches C from the right of f(X), and both limits exist and are finite.

  • What is another name for infinite discontinuities?

    -Infinite discontinuities are more commonly known as vertical asymptotes.

  • How are vertical asymptotes represented on a graph?

    -Vertical asymptotes are represented on a graph as a vertical line that the function approaches but never reaches, often resulting in the function going to positive or negative infinity.

  • What is a characteristic of a function that has an infinite discontinuity at a certain point?

    -A function has an infinite discontinuity at a certain point if the limit as X approaches that point from the left or right is positive or negative infinity.

  • What is a common algebraic scenario that leads to a removable discontinuity?

    -A common algebraic scenario that leads to a removable discontinuity is when a factor in the denominator that is zero also appears in the numerator to the same degree, but does not completely cancel out.

  • What is a famous function that has a jump discontinuity?

    -The function f(x) = |x|/x is a famous function that has a jump discontinuity at x = 0.

  • How can you identify a vertical asymptote in a rational function?

    -You can identify a vertical asymptote in a rational function by looking for a zero in the denominator that does not cancel out with a factor in the numerator.

  • Why might a piecewise function have a weird scenario for a vertical asymptote?

    -A piecewise function might have a weird scenario for a vertical asymptote because the function's definition changes at certain points, leading to different behaviors of the limits from the left and right.

Outlines
00:00
📊 Types of Discontinuities in Functions

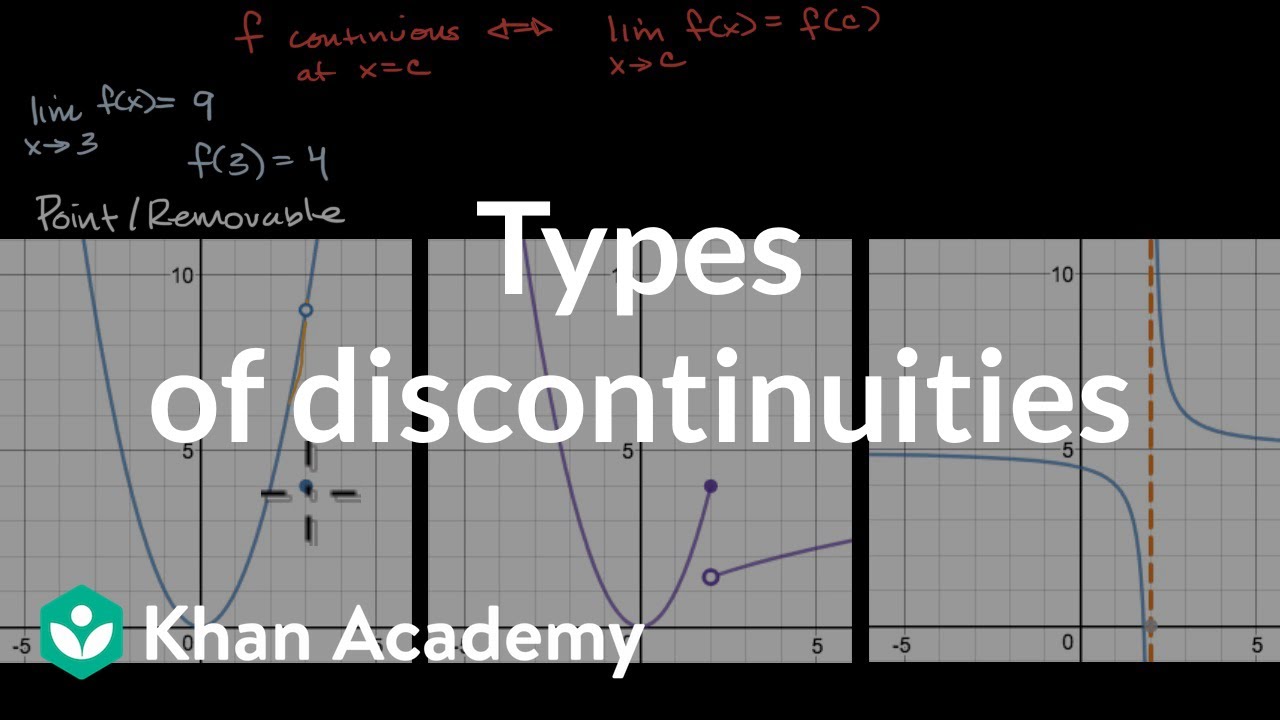
This paragraph introduces the three main types of discontinuities in functions: removable, jump, and infinite discontinuities. Removable discontinuities, also known as holes, occur when the limit exists and is finite but not equal to the function's value at that point. The paragraph provides a graphical representation and algebraic examples, such as the function f(x) = (x + 3)(x - 4) / (x + 3), which simplifies to x - 4 with the restriction that x cannot be -3, thus creating a removable discontinuity at x = -3. The concept of limits from the left and right is emphasized as a key factor in identifying these discontinuities.

05:03
🚀 Jump Discontinuities and Their Characteristics

The second paragraph delves into jump discontinuities, which are characterized by a sudden 'jump' in the function's value. Graphically, this appears as a gap where the function does not reach a certain value. The limits from the left and right as x approaches the point of discontinuity are finite but not equal, which is the defining feature of a jump discontinuity. A well-known example given is the absolute value function f(x) = |x| / x, which has a jump discontinuity at x = 0. The paragraph also discusses how to identify jump discontinuities algebraically, by looking at piecewise functions and evaluating the left and right limits.

10:06
∞ Infinite Discontinuities and Vertical Asymptotes

The final paragraph discusses infinite discontinuities, more commonly known as vertical asymptotes. These occur when the function's value approaches infinity as x approaches a certain point, or when the function 'crashes' into a vertical line. The definition of a vertical asymptote involves one-sided limits, and it is sufficient for either the limit from the left or the right to be infinite. Examples include rational functions where the denominator equals zero and does not cancel out with the numerator, such as 5x^2 / (x - 4), which has a vertical asymptote at x = 4. The paragraph also touches on piecewise functions and how to identify vertical asymptotes in such cases.

Mindmap
Keywords
💡Discontinuities
Discontinuities refer to the points on a function where the function is not defined or not continuous. In the context of the video, discontinuities are central to understanding the behavior of mathematical functions. The video discusses three types of discontinuities: removable, jump, and infinite discontinuities, each with distinct graphical representations and mathematical implications.
💡Removable Discontinuities
Removable discontinuities, also known as holes in the graph, occur when a function is undefined at a certain point but the limit exists and is finite. They are characterized by the limit from the left and right being equal and finite, yet not equal to the function's value at that point. An example from the script is the function f(x) = (x + 3)(x - 4) / (x + 3), which has a removable discontinuity at x = -3 because the function is not defined there, but the limits from both sides exist and are equal.
💡Jump Discontinuities
Jump discontinuities are points where the function has different one-sided limits. Graphically, they appear as a 'jump' from one value to another without reaching the intermediate values. The video describes this as a situation where the limit from the left is not equal to the limit from the right, resulting in a discontinuity. An example given is the absolute value function, f(x) = |x| / x, which has a jump discontinuity at x = 0, as the left-hand limit is -1 and the right-hand limit is 1.
💡Infinite Discontinuities
Infinite discontinuities, also known as vertical asymptotes, occur when the function's value approaches infinity or negative infinity as it approaches a certain point. These are typically represented by a vertical line that the function 'hits' without actually being defined at that point. The video explains that these can happen when the denominator of a rational function is zero and does not cancel out with the numerator. An example is the function f(x) = 5x^2 / (x - 4), which has an infinite discontinuity at x = 4.
💡Vertical Asymptotes
Vertical asymptotes are a specific type of infinite discontinuity where the function's value becomes unbounded (approaches positive or negative infinity) as the input approaches a certain value. They are graphically represented by a vertical line, indicating a sharp limit beyond which the function is not defined. The video mentions that vertical asymptotes can occur when the denominator of a fraction is zero and does not cancel with the numerator, as seen with the function f(x) = 1 / (x - 1).
💡Limits
In mathematical analysis, a limit is the value that a function or sequence 'approaches' as the input (or index) approaches some value. The concept of limits is fundamental in defining continuity and different types of discontinuities. The video emphasizes the importance of limits in determining whether a discontinuity is removable, jump, or infinite. For instance, for a removable discontinuity, the left and right limits must exist and be finite and not equal to the function's value at that point.
💡Piecewise Functions
Piecewise functions are functions that are defined by multiple sub-functions, each applicable to a different interval or 'piece' of the domain. These functions are relevant in the context of discontinuities as they often exhibit various types of discontinuities within their different segments. The video uses piecewise functions to illustrate how discontinuities can occur at the points where the function's definition changes.
💡Rational Functions
Rational functions are mathematical functions that can be represented as the ratio of two polynomial functions. They are often the source of discontinuities, particularly infinite discontinuities or vertical asymptotes, when the denominator equals zero. The video discusses rational functions in the context of finding discontinuities, noting that a zero in the denominator that does not cancel out with the numerator leads to a vertical asymptote.
💡Continuity
Continuity in mathematics is a property of functions that are 'uninterrupted' or 'unbroken'. A function is continuous at a point if it is defined, its limit exists, and the function's value at that point is the same as the limit. The concept of continuity is contrasted with discontinuities throughout the video to highlight where and why functions may not be smooth or uninterrupted.
💡Algebraic Functions
Algebraic functions are functions that can be expressed using algebraic techniques, typically involving polynomials. The video mentions algebraic functions in the context of finding removable discontinuities, emphasizing that zeros of the denominator that completely cancel out with the numerator lead to such discontinuities. This is demonstrated with examples like f(x) = (x + 3)(x - 4) / (x + 3).
💡One-Sided Limits
One-sided limits are a type of limit that specifically consider the behavior of a function as the input approaches a certain value from either the left (negative side) or the right (positive side). The video explains that for a jump discontinuity to occur, the left-sided limit must not equal the right-sided limit. Similarly, for a vertical asymptote, at least one of the one-sided limits (from the left or right) must be infinite.
Highlights

There are three types of discontinuities in functions: removable, jump, and infinite discontinuities.

Removable discontinuities, also known as holes, occur when the limit exists and is finite but not equal to the function's value at that point.

Jump discontinuities are characterized by the left and right limits existing and being finite, but not equal to each other.

Infinite discontinuities, or vertical asymptotes, occur when the function approaches infinity as it approaches a certain point.

The function f(x) = (x + 3)(x - 4) / (x + 3) has a removable discontinuity at x = -3.

Piecewise functions can have removable discontinuities if the limits from the left and right are equal and finite but not equal to the function's value.

The absolute value function, f(x) = |x|/x, is a famous example of a function with a jump discontinuity at x = 0.

For jump discontinuities, the function must approach different values from the left and right, indicating a 'jump' in the graph.

Vertical asymptotes can occur in piecewise functions and are identified by one-sided limits approaching infinity.

A function has an infinite discontinuity when it attempts to divide by zero, leading to an undefined expression.

The limit from the left or right of a function at a point determines the presence of a vertical asymptote.

Removable discontinuities are identified by factors in the numerator and denominator that cancel out, leaving a defined expression.

The function f(x) = 2x + 7 for x ≤ 2 and f(x) = x^2 + 8 for x > 2 has a jump discontinuity at x = 2.

Zeroes in the denominator of a rational function that do not cancel out completely result in vertical asymptotes.

Understanding the behavior of limits is crucial for identifying the type of discontinuity a function has.

The video provides examples and explanations for identifying and understanding different types of discontinuities, which is valuable for AP Calculus students.

The concept of limits is central to determining whether a discontinuity is removable, a jump, or infinite.

Transcripts

Browse More Related Video

Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

Continuity Basic Introduction, Point, Infinite, & Jump Discontinuity, Removable & Nonremovable

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

AP Calculus AB - 1.13 Removing Discontinuities

BusCalc 02 Limits and Continuity

BusCalc 01 Continuity and Discontinuities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DiscontinuitiesRemovableJumpInfiniteVertical AsymptotesFunction AnalysisLimit CalculationAlgebraic FunctionsGraph InterpretationAP CalculusEducational ContentMathematical Concepts