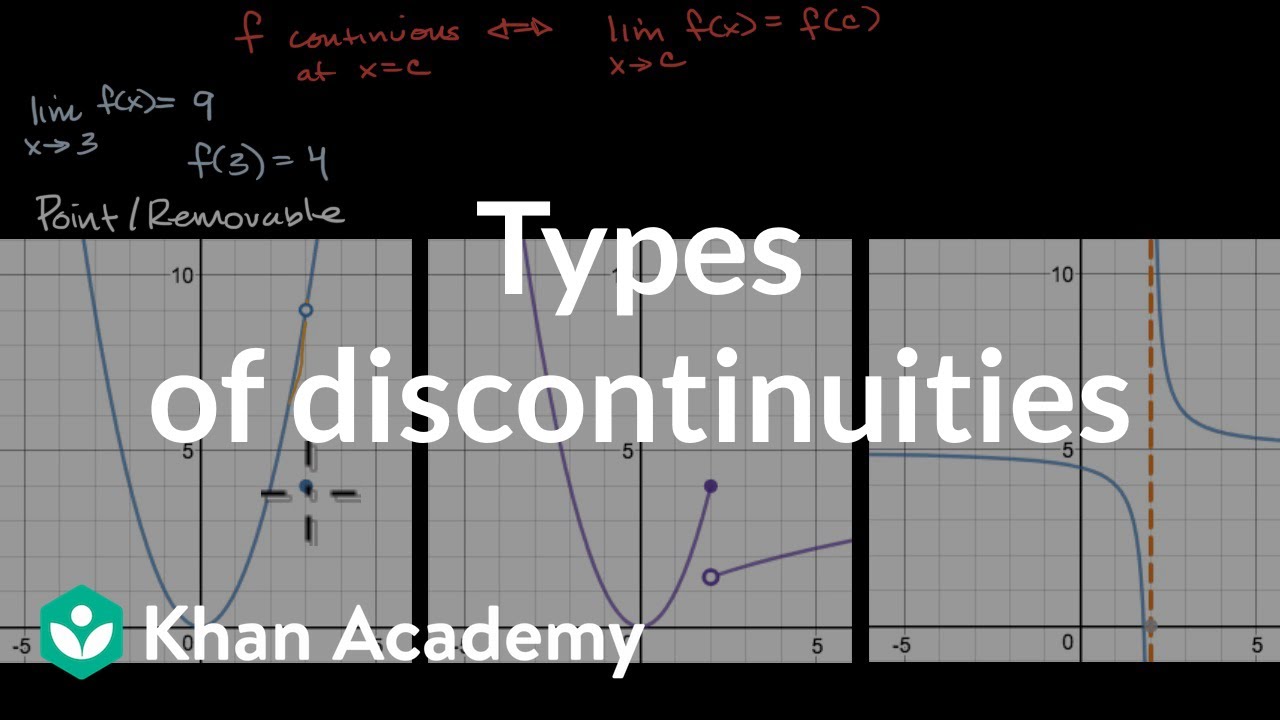
BusCalc 01 Continuity and Discontinuities
TLDRThis lesson delves into the concept of continuity in functions, contrasting it with discontinuity. The instructor begins by illustrating the continuous nature of the function f(x) = x^2, which forms a parabola when plotted on the xy-plane. The function g(x) = x / |x| is then used to demonstrate a discontinuity at x = 0, where the function's value is undefined. The four types of discontinuities are explained: point (or removable), jump, essential (or infinite), and oscillating. Polynomials are highlighted as always being continuous, while rational functions can have point or essential discontinuities, but not jump or oscillating. The lesson concludes by reinforcing the idea that a function is continuous if it can be drawn without lifting the pen, indicating no breaks or undefined points.
Takeaways
- 📈 A function is considered continuous if it can be drawn on an xy-plane without lifting the pen, meaning there are no breaks or gaps in the graph.
- 🔍 Discontinuities are points where a function is not continuous. There are four types: point, jump, essential (infinite), and oscillating discontinuities.
- 📌 Point discontinuity (also known as removable) occurs when the function is undefined at a specific point, like a hole in the graph, represented by a hollow circle.
- 🤸♂️ Jump discontinuity happens when the function jumps from one value to another at the point of discontinuity, without approaching infinity.
- ∞ Essential discontinuity (infinite discontinuity) is characterized by the function approaching positive or negative infinity on either side of the point of discontinuity.
- 🌊 Oscillating discontinuity is a complex type where the function's frequency of oscillation increases as it approaches a point, such as the origin, without settling on a particular value.
- 📐 Polynomial functions, which are sums of powers of x with natural number exponents, are always continuous, meaning they have no discontinuities anywhere in their domain.
- 🤔 Rational functions, which are ratios of two polynomials, can only have point or essential discontinuities, not jump or oscillating discontinuities.
- 🚫 For rational functions, discontinuities occur only when the denominator is zero, which is when you should check for potential discontinuities.
- 🟠 The graph of y = x^2, an even function, is a parabola with symmetry across the y-axis, representing a continuous function.
- ⚪️ The function g(x) = x / |x| has a discontinuity at x = 0, where the function is not defined, and the graph shows a hollow circle at the y-axis to indicate this.
- 📉 Rational functions can simplify to a polynomial form when factors in the numerator and denominator cancel each other out, but it's important to remember potential discontinuities caused by the original factors.
Q & A
What does it mean for a function to be continuous?
-A function is continuous if it can be drawn on an xy plane without lifting the pen, meaning it has no breaks or gaps in its graph.
What is a discontinuity?
-A discontinuity is a point where a function is not continuous, meaning there is a break or gap in the graph of the function.
What is an even function?
-An even function is one where the exponent of the variable is even, resulting in symmetry across the y-axis when graphed.
What is a parabola?
-A parabola is the shape of the graph of a quadratic function, such as y = x^2, and it is a U-shaped curve that opens upwards or downwards.
What is the difference between a point discontinuity and a jump discontinuity?
-A point discontinuity occurs when the function is undefined at a specific point, while a jump discontinuity is when the function jumps from one value to another at the discontinuity point.
What is an essential discontinuity?
-An essential discontinuity, also known as an infinite discontinuity, is when the function approaches infinity on one or both sides of the discontinuity point.
What is an oscillating discontinuity?
-An oscillating discontinuity occurs when the function's value oscillates between different values in the vicinity of a certain point, often increasing in frequency as it approaches that point.
Why are polynomials always continuous?
-Polynomials are always continuous because they are composed of terms with natural number exponents, which means their graphs have no breaks or gaps.
What types of discontinuities can a rational function have?
-A rational function can have point discontinuities or essential discontinuities, but it cannot have jump discontinuities or oscillating discontinuities.
How can you identify a potential discontinuity in a rational function?
-In a rational function, a potential discontinuity can be identified where the denominator equals zero, as this would make the function undefined at that point.
What is the significance of the factored form of a rational function in identifying discontinuities?
-The factored form of a rational function allows you to see common factors between the numerator and the denominator, which can lead to point discontinuities when those common factors are zero.
What is the role of desmos.com in graphing functions?
-Desmos.com is a tool that provides an easy-to-use graphing calculator, which can be very helpful for visualizing and understanding the behavior of functions, including their discontinuities.
Outlines
📚 Introduction to Continuity and Discontinuity
The instructor introduces the concepts of continuity and discontinuity using two example functions: f(x) = x^2 and g(x) = x/|x|. The first is a continuous function that forms a parabola, which can be drawn without lifting the pen. The second, a piecewise function, has a discontinuity at x = 0 due to division by zero. This type of discontinuity is represented visually by a hollow circle. The concept of continuity is described as being able to draw a function without lifting the pen.
📈 Point Discontinuity
This section explains point discontinuity (also called removable discontinuity) through the function f(x) = (x^2 + 4x + 3)/(x + 3). At x = -3, the denominator becomes zero, making the function undefined at that point. The numerator and denominator factors cancel, revealing the simplified form f(x) = x + 1, which is a line. The point of discontinuity is marked with a hollow circle on the graph to show where the function is undefined.
↕️ Jump Discontinuity
Jump discontinuity is explored using the function f(x) = (x+1)/|x+1|, where the function output jumps at x = -1. The graph shows a jump from negative to positive values due to the absolute value operation. The graph is undefined at x = -1, where division by zero occurs. This discontinuity results in a noticeable vertical gap between the function values.
♾️ Infinite Discontinuity
Infinite or essential discontinuity is demonstrated using the rational function f(x) = (x+3)/(x+2). The function is undefined at x = -2, leading to a division by zero. As one approaches x = -2, the function approaches positive or negative infinity, depending on the direction of approach. The graph shows a vertical asymptote, distinguishing this discontinuity from the jump type.
🔄 Oscillating Discontinuity
Oscillating discontinuity is presented with the function f(x) = sin(20)/x. As the input approaches zero, the function oscillates infinitely due to the sine function's nature. This type of discontinuity is unique because the function never stabilizes to a finite value around zero, regardless of the small interval selected.
Mindmap
Keywords
💡Continuous Function
💡Discontinuity
💡Point Discontinuity
💡Jump Discontinuity
💡Essential Discontinuity
💡Oscillating Discontinuity
💡Rational Function
💡Polynomial
💡Even Function
💡Absolute Value
💡Hollow Circle
Highlights
A function is considered continuous if it can be drawn on an xy-plane without lifting the pen.
Discontinuities are points where a function is not continuous.
The function f(x) = x^2 is an example of a continuous function, representing a parabola.
The function g(x) = x / |x| has a discontinuity at x = 0, represented by a hollow circle on the graph.
Point discontinuities, also known as removable discontinuities, occur when the function is undefined at a specific point, such as x = -3 in the function f(x) = (x^2 + 4x + 3) / (x + 3).
Jump discontinuities are seen when the function value jumps from one value to another at the point of discontinuity, as in f(x) = (x + 1) / |x + 1| at x = -1.
Essential discontinuities, or infinite discontinuities, occur when the function approaches infinity on one or both sides of the discontinuity, like in the function f(x) = (x + 3) / (x + 2) at x = -2.
Oscillating discontinuities are characterized by the function oscillating infinitely close to the point of discontinuity, such as in sin(1/x) as x approaches 0.
Polynomial functions are always continuous as they are composed of natural number powers of x.
Rational functions can have point or essential discontinuities but not jump or oscillating discontinuities.
The discontinuities in rational functions occur at the zeros of the denominator.
An even function, like f(x) = x^2, exhibits symmetry across the y-axis.
The shape of the function f(x) = x^2 is a parabola, which is a U-shaped curve.
For the function g(x) = x / |x|, positive values of x result in a function value of 1, while negative values result in -1.
The function f(x) = (x^2 + 4x + 3) / (x + 3) has a point discontinuity at x = -3, where the denominator becomes zero.
The function f(x) = (x + 1) / |x + 1| has a jump discontinuity at x = -1, where the function jumps from one value to another.
In the function f(x) = (x + 3) / (x + 2), as x approaches -2 from either side, the function approaches infinity, indicating an essential discontinuity.
The sine function, when divided by x, such as in sin(20)/x, exhibits an oscillating behavior as x approaches 0, leading to an oscillating discontinuity.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: