AP Calculus AB - 1.13 Removing Discontinuities

Daniel Bortnick
12 Oct 202010:47
EducationalLearning
32 Likes 10 Comments

TLDRThis video script by Mr. Bortnick covers the topic of removing discontinuities in AP Calculus AB, focusing on unit 1 limits and continuity. It explains the concept of a removable discontinuity, often referred to as a 'hole' in a graph, and how it occurs when the limit exists but doesn't equal the function's value at that point. The script guides through three problems, demonstrating how to identify removable discontinuities, find the x and y values of the 'hole', and determine the necessary function value to achieve continuity. It concludes with practice problems and test prep suggestions for further understanding.

Takeaways
  • 📚 The lecture is about 'Removing Discontinuities' in the context of AP Calculus AB, specifically focusing on Unit 1, Limits and Continuity.
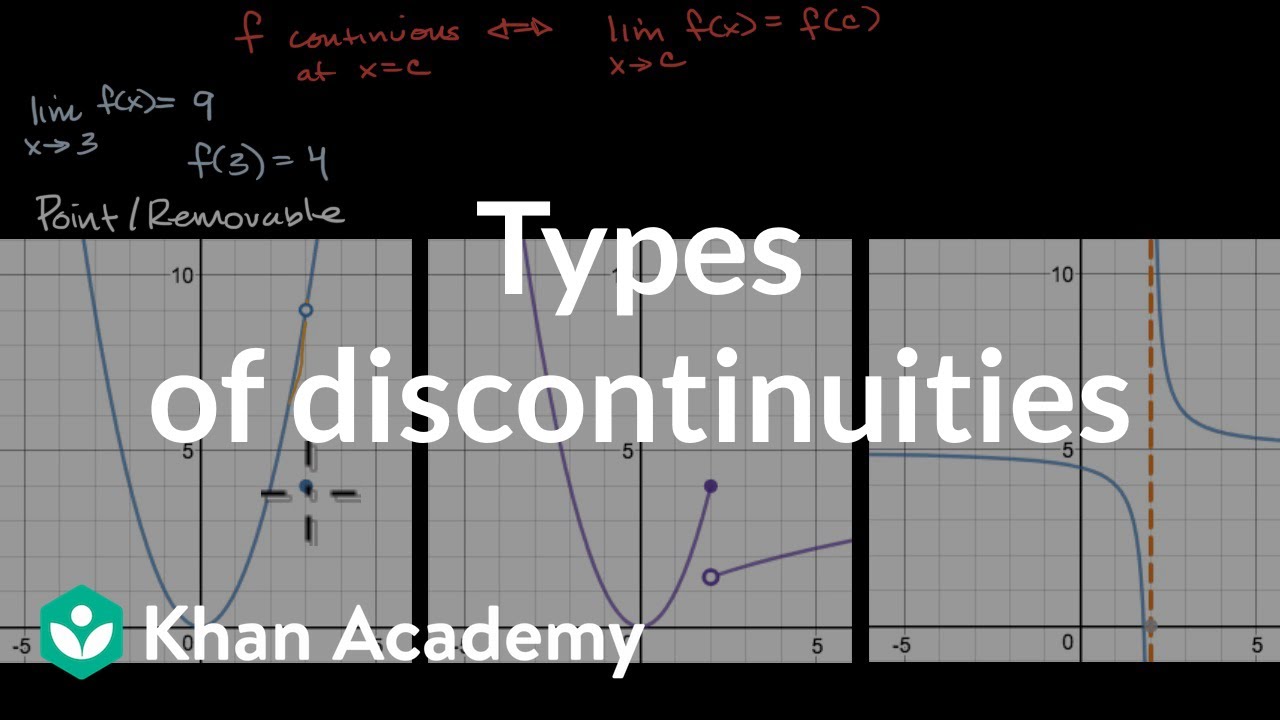
  • 🕳 A 'removable discontinuity' is described as a 'hole' in the graph of a function, where the limit exists but is not equal to the function's value at that point.
  • 🔍 The formal definition of a removable discontinuity is a point where the limit as x approaches c of f(x) exists, but the limit is not equal to f(c).
  • 📈 The concept is visually represented in a graph where the function approaches a certain y-value from both the left and right but does not include that point.
  • 🔧 A removable discontinuity can be 'fixed' by defining the function's value at the point of discontinuity to match the limit.
  • 📝 The first problem involves a function with a hole at x = 1, where the function is (x^2 - 1) / (x - 1), and the hole's y-value is found to be 2.
  • 🔑 The second problem discusses a continuous function f(x) = (x^2 + 6x + 8) / (x + 4), where f(-4) must equal -2 to remove the discontinuity at x = -4.
  • 🧩 The third problem involves a piecewise function that needs a specific value of 'a' to be continuous at x = 6, which is determined to be 9 by factoring and simplifying the function.
  • 📉 The process of solving these problems involves factoring, understanding limits, and recognizing how to fill in the 'hole' to achieve continuity.
  • 📚 Additional resources such as practice problems and test prep problems are provided for further understanding and application of the concepts.
  • 🗓 The lecture concludes with a reminder to check out the provided resources and a wish for a good rest of the day.
Q & A

  • What is a removable discontinuity in the context of calculus?

    -A removable discontinuity is a point on a graph where the function is not defined, often represented by an open circle. It is called removable because the discontinuity can be 'fixed' by redefining the function's value at that point, thus making the graph continuous.

  • How can you identify a removable discontinuity in a function's graph?

    -A removable discontinuity can be identified by a hole or an open circle in the graph of the function. This occurs where the function is not defined, but the limit exists as the variable approaches the point of discontinuity.

  • What is the mathematical definition of a removable discontinuity?

    -Mathematically, a removable discontinuity occurs at a point 'c' in the domain of a function 'f(x)' where the limit as x approaches c exists, but the limit is not equal to the function's value at c, i.e., lim(x->c) f(x) exists but is not equal to f(c).

  • In the given script, what is the function f(x) for problem number one?

    -The function f(x) for problem number one is f(x) = (x^2 - 1) / (x - 1).

  • How do you find the x-value of the hole in the graph of the function given in problem number one?

    -To find the x-value of the hole, you set the denominator of the function equal to zero, which in this case is x - 1 = 0, resulting in x = 1.

  • What is the y-value of the hole for the function in problem number one?

    -The y-value of the hole can be found by simplifying the function after canceling the common factor in the numerator and denominator, which results in f(x) = x + 1. Plugging in x = 1 gives f(1) = 2.

  • What does the function f(x) represent in problem number two of the script?

    -In problem number two, the function f(x) is given as f(x) = (x^2 + 6x + 8) / (x + 4), and it is continuous for all real numbers except where the denominator is zero, which is at x = -4.

  • What value must f(-4) have for the function in problem number two to be continuous?

    -For the function to be continuous at x = -4, f(-4) must equal the limit of the function as x approaches -4, which is found by simplifying the function to x + 2 and evaluating it at x = -4, resulting in f(-4) = -2.

  • What is the function f(x) in problem number three, and what is its piecewise definition?

    -In problem number three, the function f(x) is defined piecewise as f(x) = (x^2 - 3x - 18) / (x - 6) when x is not equal to 6, and f(x) = a when x is equal to 6.

  • What value of 'a' makes the function in problem number three continuous at x = 6?

    -To make the function continuous at x = 6, the value of 'a' must be such that it fills the hole created by the discontinuity. By factoring and simplifying the function, we find that a must equal 9, as 6 + 3 = 9.

  • What are the steps to determine the value of 'a' in problem number three?

    -First, factor the numerator of the function to find common factors with the denominator. Then, cancel out the common factor (x - 6) and determine the value that makes the simplified expression equal to 'a' when x = 6. In this case, it is 6 + 3, which equals 9.

Outlines
00:00
📚 Introduction to Removing Discontinuities

In this segment, Mr. Bortnick introduces the topic of removing discontinuities in the context of AP Calculus AB, specifically focusing on unit 1, limits, and continuity. He begins by reviewing the concept of a removable discontinuity, which is often referred to as a 'hole' in a graph. He explains that a removable discontinuity occurs when the limit exists as x approaches a certain point 'c', but the function's value at 'c' does not match the limit. He emphasizes that this type of discontinuity can be 'removed' by filling in a single point on the graph. Mr. Bortnick then moves on to problem-solving, starting with a function that has a hole in its graph, guiding students through the process of finding the x and y values of the hole by factoring and simplifying the function.

05:01
🔍 Analyzing Continuity and Discontinuities

The second paragraph delves deeper into the concept of continuity and discontinuities, using a function that is defined to be continuous for all real numbers except at a specific point where the function is undefined due to a denominator of zero. Mr. Bortnick illustrates how to identify and address removable discontinuities by factoring the numerator and denominator of a rational function and then simplifying it. He demonstrates this by taking a function with a potential discontinuity at x = -4 and showing that by finding the limit as x approaches -4, the discontinuity can be removed by defining f(-4) to be the value that makes the function continuous at that point. This involves understanding the behavior of the function around the point of discontinuity and ensuring that the function's value at that point matches the limit of the function as it approaches the point.

10:02
🔧 Fixing Discontinuities in Piecewise Functions

In the final paragraph, Mr. Bortnick discusses the continuity of a piecewise function, specifically focusing on how to determine the value of 'a' that would make the function continuous at x = 6. He starts by factoring the numerator of the function, which reveals a discontinuity at x = 6 due to the denominator being zero at that point. By simplifying the function and setting it equal to 'a' at the point of discontinuity, he shows that the value of 'a' must be 9 to ensure the function is continuous. This process involves understanding the algebraic manipulation of piecewise functions and recognizing how to adjust the function's definition to eliminate discontinuities. Mr. Bortnick concludes by encouraging students to practice with additional problems and to review test prep materials to prepare for the AP exam.

Mindmap
Keywords
💡Removable Discontinuity
A removable discontinuity refers to a point on a graph where the function is not defined, often represented by an open circle, but the limit exists at that point. In the context of the video, it is a type of discontinuity that can be 'removed' by defining the function at that point, thus making the graph continuous. For example, the script discusses how a removable discontinuity can occur in the function \( f(x) = rac{x^2 - 1}{x - 1} \) at \( x = 1 \), where the function is undefined, but the limit exists and equals 2.
💡Limit
The limit is a fundamental concept in calculus that describes the value that a function approaches as the input (x) approaches a certain value. In the video, the limit is used to define and identify removable discontinuities. For instance, the script explains that at a removable discontinuity, the limit as x approaches a certain value 'c' exists but is not equal to the function's value at 'c', hence creating a discontinuity.
💡Continuity
Continuity in calculus means that a function has no breaks, jumps, or holes in its graph. The video's theme revolves around understanding and identifying points of discontinuity to then make the function continuous. The script uses the concept of continuity to explain how filling in a point at a removable discontinuity can make a function continuous, as seen in the function \( f(x) = x^2 + 6x + 8 \) when \( x eq -4 \).
💡Factoring
Factoring is an algebraic method used to express a polynomial as the product of its factors. In the script, factoring is used as a technique to identify removable discontinuities by simplifying the function and finding values that make the denominator zero. For example, the function \( f(x) = rac{x^2 - 1}{x - 1} \) is factored into \( rac{(x + 1)(x - 1)}{x - 1} \) to reveal the discontinuity at \( x = 1 \).
💡Hole
In the context of the video, a 'hole' refers to a point on a graph where the function is not defined, which is a visual representation of a removable discontinuity. The script explains that a hole is where an open circle appears on the graph, indicating the absence of a function value at that point, but the limit exists around it.
💡Graph
A graph is a visual representation of a function's behavior, plotting the input values on the x-axis against the output values on the y-axis. The video script uses graphs to illustrate the concept of discontinuities, showing how removable discontinuities appear as holes or open circles on the graph and how they can be fixed to achieve continuity.
💡AP Calculus
AP Calculus is a high school course and exam that covers college-level calculus topics. The video script is from a lesson teaching AP Calculus AB, which is focused on the concepts of limits and continuity, as part of the curriculum's Unit 1. The script is specifically discussing the topic of removing discontinuities, which is a key concept in the course.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs, with the requirement that each input is related to exactly one output. The video script frequently refers to functions, especially in the context of finding discontinuities and making them continuous by defining the function at those points.
💡Denominator
The denominator is the bottom part of a fraction, which cannot be zero as it would make the fraction undefined. In the script, the denominator is critical when discussing discontinuities, as a zero denominator indicates a point of potential discontinuity, such as in the function \( f(x) = rac{x^2 + 6x + 8}{x + 4} \) where \( x eq -4 \) to avoid an undefined expression.
💡Piecewise Function
A piecewise function is a function that is defined by multiple pieces, each with its own formula, applied over different intervals of the domain. The script discusses a piecewise function to illustrate how to make a function continuous at a specific point by defining the value of 'a' that makes the function continuous at \( x = 6 \).
💡Continuous Function
A continuous function is one where the graph has no breaks, holes, or jumps. The video script aims to teach how to identify and remove discontinuities to achieve a continuous function. For example, the script explains that if a function is defined to fill in the hole at a removable discontinuity, it becomes a continuous function.
Highlights

Introduction to the topic of removing discontinuities in the context of AP Calculus AB.

Definition of a removable discontinuity as a 'hole' in a graph.

Explanation of when a removable discontinuity occurs in a function's graph.

The formal mathematical definition of a removable discontinuity.

Visual identification of removable discontinuities from the graph's perspective.

The concept that a removable discontinuity can be 'filled in' to achieve continuity.

Problem-solving approach for identifying the x-value of a hole in a graph.

Use of algebraic factoring to find discontinuities in a function.

Method to find the y-value of a hole by simplifying the function after factoring.

Application of the concept to a specific function with a removable discontinuity.

Guidance on how to graph a function with a removable discontinuity.

Explanation of a function's continuity and its implications for graphing.

Identification of a function's potential discontinuity based on the denominator.

Process of determining the value of f(x) at a point of discontinuity to ensure continuity.

Technique to simplify a function by canceling out common factors to find the limit.

The importance of matching the function's value at a point to remove discontinuity.

Approach to determine the value of 'a' for a piecewise function to achieve continuity.

Final summary of the steps and methods used to remove discontinuities in functions.

Encouragement to practice with provided problems and resources for further learning.

Transcripts

Browse More Related Video

Calculus AB/BC – 1.13 Removing Discontinuities

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus

Three Types of Discontinuities in Functions

Math 11 - Sections 1.1-1.2

Continuity

Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusLimitsContinuityRemovable DiscontinuitiesMath EducationHole in GraphFunction AnalysisEducational ContentMath ProblemsTeaching Method