17. Simple Harmonic Motion
TLDRIn this comprehensive lecture, Professor Ramamurti Shankar delves into the intricacies of stable equilibrium and harmonic motion, using the mass-spring system and a twisted bar as illustrative examples. He explains the concept of restoring forces and torques, and how they relate to the system's natural frequency ω, derived from the square root of the ratio k/m (spring constant to mass) or κ/I (torque constant to moment of inertia) for rotational systems. The professor further explores the general solution to the simple harmonic motion equation, emphasizing the role of complex exponentials and how they can represent both trigonometric functions and real-valued solutions, important for physical phenomena. He also addresses the impact of friction on oscillating systems, leading to damped oscillations, and introduces the concept of a driven oscillator, where an external force influences the system's behavior. Throughout the lecture, Shankar employs mathematical derivations and physical insights to clarify the underlying principles, providing students with a deeper understanding of oscillations and their applications in physics.
Takeaways
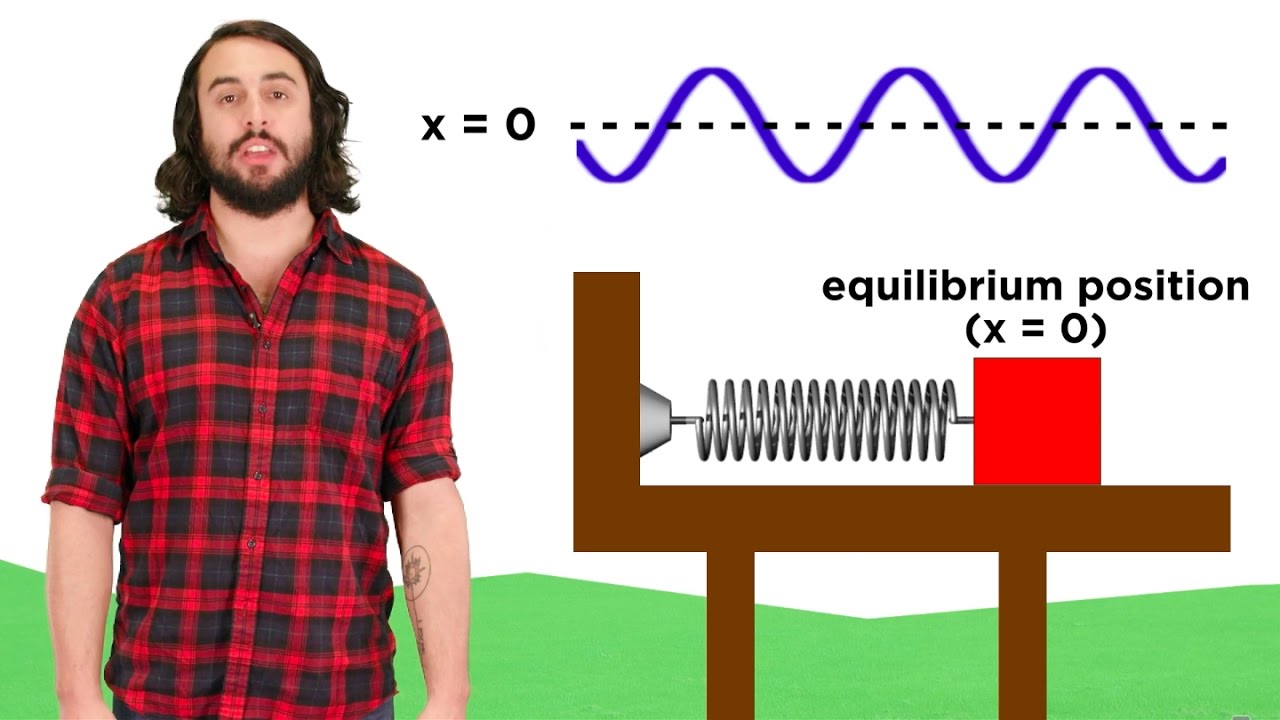
- 📚 The concept of stable equilibrium is introduced where a system, when disturbed, oscillates back to its original state, exemplified by a mass on a spring.
- 🌀 The restoring force in simple harmonic motion is described by the equation F = -kx, where k is the spring constant and x is the displacement from the equilibrium position.
- 📐 The solution to the equation of motion for a mass-spring system is given by x(t) = A cos(ωt - φ), where A is the amplitude, ω is the angular frequency, and φ is the phase angle.
- 🔄 The general form of simple harmonic motion is derived from the properties of trigonometric functions and their derivatives.
- ⚙️ A second example of stable equilibrium is given by a torsional pendulum, where the restoring torque is proportional to the angle of twist θ.
- 🔗 The restoring torque in a torsional system is expressed as -κθ, where κ is the torsional constant, which must be determined experimentally or given in the problem.
- 🧮 For a pendulum, the restoring torque is found using the force of gravity acting on the mass and the torque is given by -mglθ, where m is the mass, g is the acceleration due to gravity, and l is the length of the pendulum.
- 📉 The moment of inertia for a point mass at a distance from the pivot is ml^2, and this is used to find the angular frequency ω for the pendulum's oscillation.
- 🤔 The importance of understanding the system's properties, such as κ in a torsional pendulum, is emphasized as it is not a universally known value and must be derived or provided for the specific problem.
- 📚 Complex numbers and Euler's formula are introduced as a powerful tool for solving problems involving oscillations, as they allow for the combination of trigonometric functions into a single complex exponential form.
- 🔢 The polar form of complex numbers is discussed, highlighting the ability to represent complex numbers in both Cartesian (x + iy) and polar (r e^(iφ)) forms.
Q & A
What is the restoring force in a mass-spring system when the mass is displaced from its equilibrium position?
-The restoring force in a mass-spring system is given by F = -kx, where 'k' is the spring constant and 'x' is the displacement from the equilibrium position. This force acts to bring the mass back to its equilibrium position.
What is the general form of the solution to the equation of motion for a mass-spring system?
-The general form of the solution to the equation of motion for a mass-spring system is A*cos(ωt - φ), where 'A' is the amplitude, 'ω' is the angular frequency, and 'φ' is the phase constant.
How does the restoring torque in a twisted bar system relate to the angle of twist θ?
-The restoring torque in a twisted bar system is proportional to the angle of twist θ and acts in the opposite direction to untwist the bar. The mathematical expression for the restoring torque is -κθ, where 'κ' is a constant related to the bar's torsional properties.
What is the equation of motion for a simple pendulum?
-The equation of motion for a simple pendulum, when displaced by an angle θ, is I * d^(2)θ/dt^(2) = -κθ, where 'I' is the moment of inertia, 'κ' is a constant related to the gravitational force and the length of the pendulum, and 'θ' is the angular displacement from the vertical position.
What is the significance of the complex exponential function e^(iθ) in the context of oscillations?
-The complex exponential function e^(iθ) is significant because it unifies the trigonometric functions sine and cosine. It allows for the representation of oscillations in a complex number form, which can simplify the analysis of oscillatory systems, particularly when dealing with complex numbers or when the system is underdamped, critically damped, or overdamped.
How does the Euler's formula relate to the trigonometric functions?
-Euler's formula states that e^(iθ) = cos(θ) + i*sin(θ), which shows a direct relationship between the exponential function and the trigonometric functions. It also implies that e^(-iθ) = cos(θ) - i*sin(θ), which are the complex conjugates of each other.
What is the physical requirement for the position 'x' in a mass-spring system?
-The physical requirement for the position 'x' in a mass-spring system is that it must be a real function. This is because in the real world, the displacement of the mass cannot be complex; it must be a real value representing the actual distance from the equilibrium position.
How does the presence of friction in a mass-spring system affect the equation of motion?
-The presence of friction adds a damping term to the equation of motion. The equation becomes mx'' + bx' + kx = 0, where 'b' is the friction coefficient. This results in an exponential decay of the oscillation, as the system loses energy due to the frictional force.
What is the term for the property of a linear equation that allows you to combine solutions?
-The property is called 'superposition'. It states that if x1 and x2 are solutions to a linear differential equation, then any linear combination of these solutions (such as A*x1 + B*x2) is also a solution to the equation.
What is the difference between underdamped, critically damped, and overdamped systems?
-Underdamped systems have oscillatory behavior with a decaying amplitude. Critically damped systems have just enough damping to avoid oscillation, leading to the fastest return to equilibrium without overshooting. Overdamped systems have more damping than critical, resulting in a slow return to equilibrium without oscillation.
How can you find the values of A and B in the solution for a damped mass-spring system?
-To find the values of A and B, you would use the initial conditions of the system. Typically, you would use the initial position (x at t=0) and initial velocity (dx/dt at t=0) to set up two equations and solve for A and B in the solution x(t) = A*e^(-αt) + B*e^(-βt), where α and β are the roots of the characteristic equation for the damped system.
Outlines
😀 Introduction to Stable Equilibrium and Simple Harmonic Motion
Professor Shankar begins by discussing stable equilibrium, using a mass on a spring as an example. He explains the restoring force and how it relates to Newton's law, leading to the equation of motion for simple harmonic motion. The general solution to this equation is presented as A cos ωt - φ, where A is the amplitude, ω is the angular frequency, and φ is the phase. A second example involves a bar suspended by a cable, introducing the concept of restoring torque.
🔍 Restoring Torque and Its Mathematical Expression
The professor delves into the expression for restoring torque, which is a function of the displacement angle θ and is proportional to θ with a constant κ. The equation relating torque to the moment of inertia and angular acceleration is established. The role of κ in rotation problems is compared to that of the spring constant k in linear problems. The process of finding κ for a pendulum is described, including the calculation of the torque due to gravity and the moment of inertia for small angles.
📚 Complex Numbers and Euler's Formula in Oscillation Analysis
Professor Shankar introduces the use of complex numbers and Euler's formula, e^(iθ) = cos θ + i sin θ, as a powerful tool for analyzing oscillations. He explains that the complex exponential function can replace trigonometric functions in the context of simple harmonic motion. The polar form of complex numbers and the concept of complex conjugation are discussed, along with their implications for the general solution to the equation of motion.
🔧 Application of Complex Exponentials in Solving Differential Equations
The professor demonstrates the use of complex exponentials in solving the differential equation for a damped harmonic oscillator. He explains the process of making an ansatz, or a tentative guess, and how to adjust the parameters to satisfy the equation. The importance of understanding the physical requirement of real solutions is emphasized, and the process of finding the complex conjugate of a solution is outlined.
🌀 Superposition Principle and Linear Equations in Physics
The concept of superposition is introduced, which is a fundamental property of linear equations. The professor shows that if two functions are solutions to a linear differential equation, any linear combination of them is also a solution. This leads to the idea that linear equations have an infinite number of solutions, which can be constructed from a few basic solutions. The difference between linear and non-linear equations is highlighted.
🔄 Damped Oscillations and the Role of Friction
The discussion moves to damped oscillations, where the effect of friction is considered. The professor derives the equation of motion for a system with friction and explains how to solve it using complex exponentials. He addresses the concern about imaginary numbers in the solution and shows how to obtain real solutions by considering the complex conjugate and ensuring that the coefficients A and B are complex conjugates of each other.
🚗 Applications in Real World: Damping in Car Shock Absorbers
The professor illustrates the practical application of damping in car shock absorbers. He describes the three types of damping: underdamped (where oscillation decays over time), critically damped (where there's no oscillation and the system returns to equilibrium quickly), and overdamped (where the system returns to equilibrium very slowly without oscillation). The ideal damping for shock absorbers is also discussed.
🎓 Final Topic: Driven Oscillator and Complex Analysis
The lecture concludes with the topic of a driven oscillator, where an external force is applied to the system. The professor uses complex analysis to solve the equation for a driven oscillator, introducing the concept of impedance and showing how to find the amplitude and phase shift of the oscillation. He emphasizes the importance of understanding the underlying mathematics and the physical interpretation of the results.
Mindmap
Keywords
💡Stable equilibrium
💡Simple harmonic motion
💡Restoring force
💡Angular frequency (ω)
💡Damping
💡Driven oscillator
💡Complex numbers
💡Torque
💡Moment of inertia (I)
💡Linear equation
💡Eigenfunctions and eigenvalues
Highlights
Professor Shankar explains the concept of stable equilibrium and simple harmonic motion using a mass on a spring as an example.
Derivation of the equation for simple harmonic motion, d^(2)x/dt^(2) = -ω^(2)x, where ω is the angular frequency, is discussed.
The general solution to the simple harmonic motion equation is given as A cos ωt - φ, where A is the amplitude and φ is the phase.
Introduction of a second example involving a bar suspended by a cable, which exhibits twisting behavior when disturbed from equilibrium.
Discussion on the restoring torque in the case of the twisted bar, which is proportional to the angle of twist θ and is represented as -κθ.
The equation for the suspended bar's motion is derived as I d^(2)θ/dt^(2) = -κθ, where I is the moment of inertia and κ is a constant.
Professor Shankar demonstrates how to find the constant κ for a pendulum by calculating the torque and using the parallel axis theorem for the moment of inertia.
The relationship between angular frequency ω, the moment of inertia I, and the constant κ is established for the pendulum problem.
An irregularly shaped object hanging from a nail is used to illustrate the concept of the center of mass and its effect on the restoring torque.
The restoring torque for the irregular object is derived as mgl sin θ, which is approximated as mgl θ for small angles.
Professor Shankar emphasizes the importance of understanding the underlying physics to determine the restoring torque in various problems.
The Euler formula e^(iθ) = cos θ + i sin θ is introduced as a fundamental concept for understanding complex oscillations.
The complex conjugate property is explained, showing how it can be used to derive trigonometric identities from the exponential form.
The polar form of a complex number is discussed, highlighting its importance in representing the magnitude and phase of oscillations.
Ansatz, a German term for a tentative guess, is used to solve the equation d^(2)x/dt^(2) = -ω^(2)x using complex exponentials.
Superposition principle is introduced, stating that the sum of two solutions to a linear equation is also a solution.
The importance of linearity in differential equations is emphasized, showing how it allows for an infinite number of solutions through combinations of base solutions.
The concept of complex conjugate is used to ensure that the solution for the mass-spring system is real, despite involving complex numbers in the process.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: