Static Equilibrium: concept
TLDRThe video script introduces the concept of static equilibrium, which involves a system that is not moving and where all forces are balanced. It emphasizes the importance of considering all forces and torques in three dimensions (x, y, and z) for rigid objects. The speaker outlines a general strategy for solving static equilibrium problems: identifying all forces and their locations, constructing force and torque equations, and performing algebraic calculations to find unknowns. An example using a balance scale illustrates the process, where forces due to mass, the normal force at the pivot point, and the board's weight are considered. The example demonstrates how to set up equations for forces in the y-direction and torques around the pivot point, ensuring they balance out to zero. The summary encourages viewers to follow along with examples and practice the algebraic process for a deeper understanding of static equilibrium.
Takeaways
- 📚 **Static Equilibrium Defined**: A state where a system is not moving and everything is balanced.
- ⚖️ **Balance of Forces**: For rigid objects, all forces must be balanced in all directions (x, y, and z).
- 🔄 **Torque Balance**: All torques must be balanced at all pivot points, with the sum of torques equaling zero.
- 📐 **Identify Forces**: The first step in solving a static equilibrium problem is to identify all forces and their locations.
- 🔍 **Don't Miss Forces**: Ensure to include all forces, including those at pivot points, to avoid incorrect answers.
- 📊 **Construct Equations**: After identifying forces, construct force equations and a torque equation for the problem.
- 🧮 **Algebra Required**: Perform algebra and plug in numbers to solve for unknowns.
- 🔄 **Torque Directionality**: Consider the direction of forces when calculating torques, as they can be positive or negative.
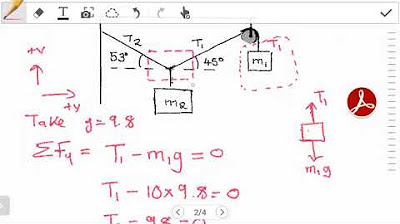
- 📈 **Sum of Forces in Y**: In the example, the sum of forces in the y-direction is crucial for balance.
- 🔵 **Label Forces**: Clearly label forces with information like mass and gravitational force (m1g, m2g, mbg).
- 🔴 **Pivot Point Consideration**: Choose an appropriate pivot point for torque calculations and consider distances from it.
- 🔢 **Solve for Unknowns**: Use the constructed equations to plug in known values and solve for the unknowns.
Q & A
What does the term 'static' refer to in the context of static equilibrium?
-In the context of static equilibrium, 'static' refers to a state where there is no movement or motion.
What is the meaning of 'equilibrium' in the context of static equilibrium?
-Equilibrium in the context of static equilibrium means a state where all forces and torques are balanced, resulting in no net force or rotation.
Why is it important to consider all directions when analyzing forces on a rigid object?
-Considering all directions (x, y, z) is important because it ensures that all forces acting on a rigid object are accounted for, ensuring that the object remains in equilibrium.
What is the significance of torque in the context of static equilibrium?
-Torque is significant because it represents the rotational force acting on an object. For an object to be in static equilibrium, the sum of all torques around any pivot point must be equal to zero.
Why is it crucial to identify all forces and their locations when solving a static equilibrium problem?
-Identifying all forces and their locations is crucial to ensure accuracy in solving the problem. Missing any forces can lead to incorrect results as the balance of forces and torques is critical for static equilibrium.
What is the role of the pivot point in static equilibrium problems?
-The pivot point is the location around which torques are calculated. It is where the object is supported or fixed, and it is crucial for determining the distances and directions of forces for torque calculations.
How does the mass of the board itself affect the static equilibrium in the given example?
-The mass of the board affects the static equilibrium because it contributes to the overall weight of the system. Its weight acts at the center of gravity of the board, which must be considered in the force and torque equations.
What is the first step in setting up force equations for a static equilibrium problem?
-The first step is to identify and label all forces acting on the system, including their magnitudes and the points of application, ensuring that no forces are overlooked.
What does the normal force represent in the context of the balance scale example?
-In the context of the balance scale example, the normal force represents the upward force exerted by the pivot point that supports the board and prevents it from falling.
How do you determine the direction of the forces when setting up the force equation in the y-direction?
-The direction of forces is determined based on their effect on the object. In the y-direction, forces acting downward (due to gravity) are considered negative, while the normal force, acting upward, is considered positive.
What is the process for setting up the torque equation in a static equilibrium problem?
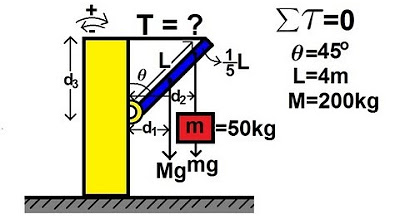
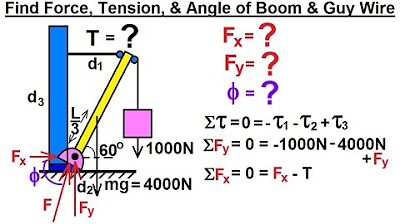
-To set up the torque equation, you first choose a pivot point, label all forces with their magnitudes and directions, determine the distances of the forces from the pivot point, and then calculate the sum of the torques, ensuring that the torques balance out to zero.
What is the final step in solving a static equilibrium problem after setting up the equations?
-The final step is to perform the algebraic manipulation and plug in the known values to solve for the unknowns, followed by checking the answer to ensure it is consistent with the conditions of static equilibrium.
Outlines
🔍 Understanding Static Equilibrium
This paragraph introduces the concept of static equilibrium by defining key terms 'static' and 'equilibrium'. It explains that in static equilibrium, a system is not moving and all forces are balanced. The importance of considering forces in all three dimensions (x, y, z) is highlighted. The paragraph also emphasizes the need to account for torques at pivot points and provides a general strategy for solving static equilibrium problems, which includes identifying all forces and their locations, constructing force and torque equations, and performing the necessary algebra to solve for unknowns. An example using a balance scale is given to illustrate the process.
📐 Calculating Torques in Static Equilibrium
The second paragraph delves into the process of calculating torques for a static equilibrium problem. It outlines the steps needed to create torque equations, which include labeling all forces, choosing a pivot point, determining distances from the pivot point for each force, and considering the directions of the forces. The paragraph clarifies that forces at the pivot point do not contribute to the torque equation due to their zero distance from the pivot. It then explains how to account for the direction of forces when summing torques, with counterclockwise torques being positive and clockwise torques being negative. The paragraph concludes by stating that the sum of torques must equal zero, and it suggests that the next steps would involve plugging in known values and solving for unknowns.
Mindmap
Keywords
💡Static Equilibrium
💡Forces
💡Torque
💡Pivot Point
💡Normal Force
💡Center of Gravity
💡Direction
💡Force Diagrams
💡Algebra
💡Balance Scale
💡Sum of Forces
💡Sum of Torques
Highlights
Static equilibrium is a concept where a system is not moving and everything is balanced
For rigid objects, all forces must be balanced in all directions (x, y, z)
All torques must also be balanced at all pivot points for rigid objects
The sum of the torques must equal 0
When approaching a static equilibrium problem, identify all forces and their locations
Don't forget pivot point forces that hold a pivot as a fixed point
After identifying forces, construct force equations and a torque equation
Use algebra to plug in numbers and solve for unknowns
Check your answer after solving the problem
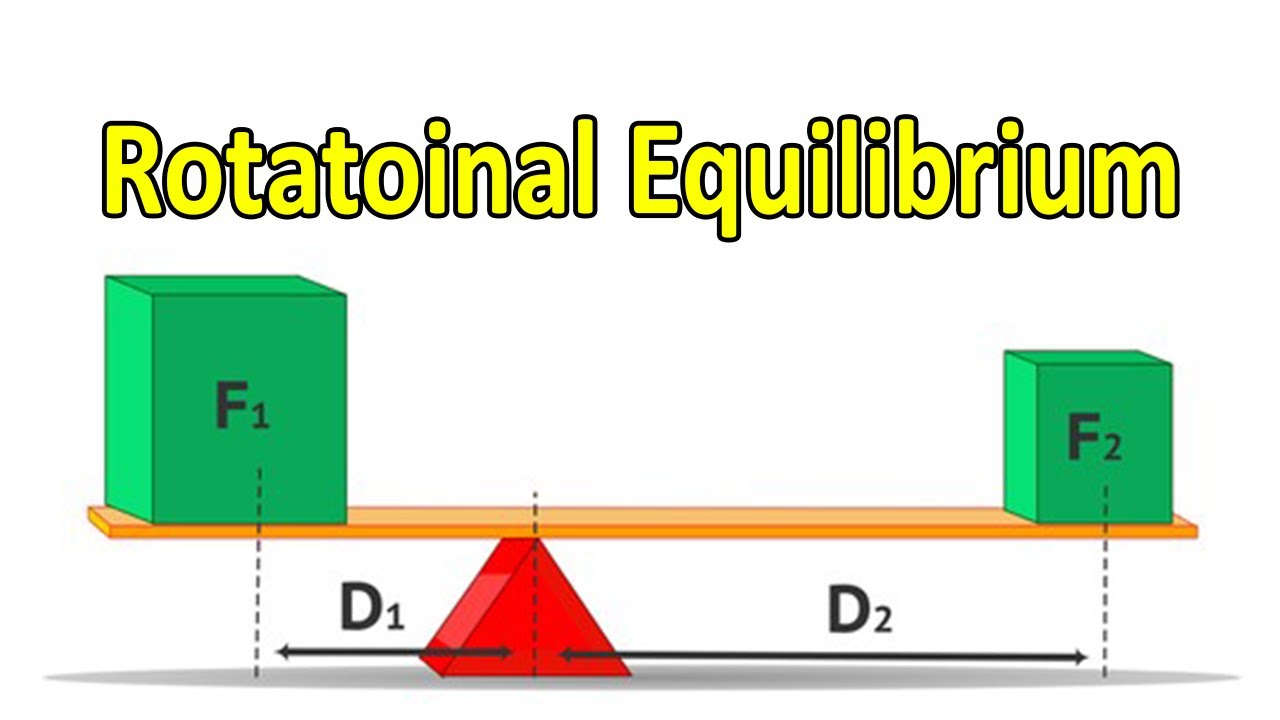
Example problem involves a balance scale with a long rod and masses on either side
Label forces with as much information as possible (e.g. m1g, m2g, mbg for mass forces, N for normal force)
Sum of forces in x-direction is 0 for this problem
No forces in z-direction for this 2D problem
Sum of forces in y-direction is the normal force minus the mass forces (m1g + m2g + mbg) equals 0
For torques, choose a pivot point (in this case the center of the rod)
Determine distances of forces from the pivot point (r1, r2, etc.)
Forces at the pivot point (normal force, weight of board) have a distance of 0 and do not affect torques
Include torque contributions from each mass force in the sum of torques equation, with appropriate signs for direction
The sum of torques must equal 0 for equilibrium
Plug in known values and solve the force and torque equations to find unknowns
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: