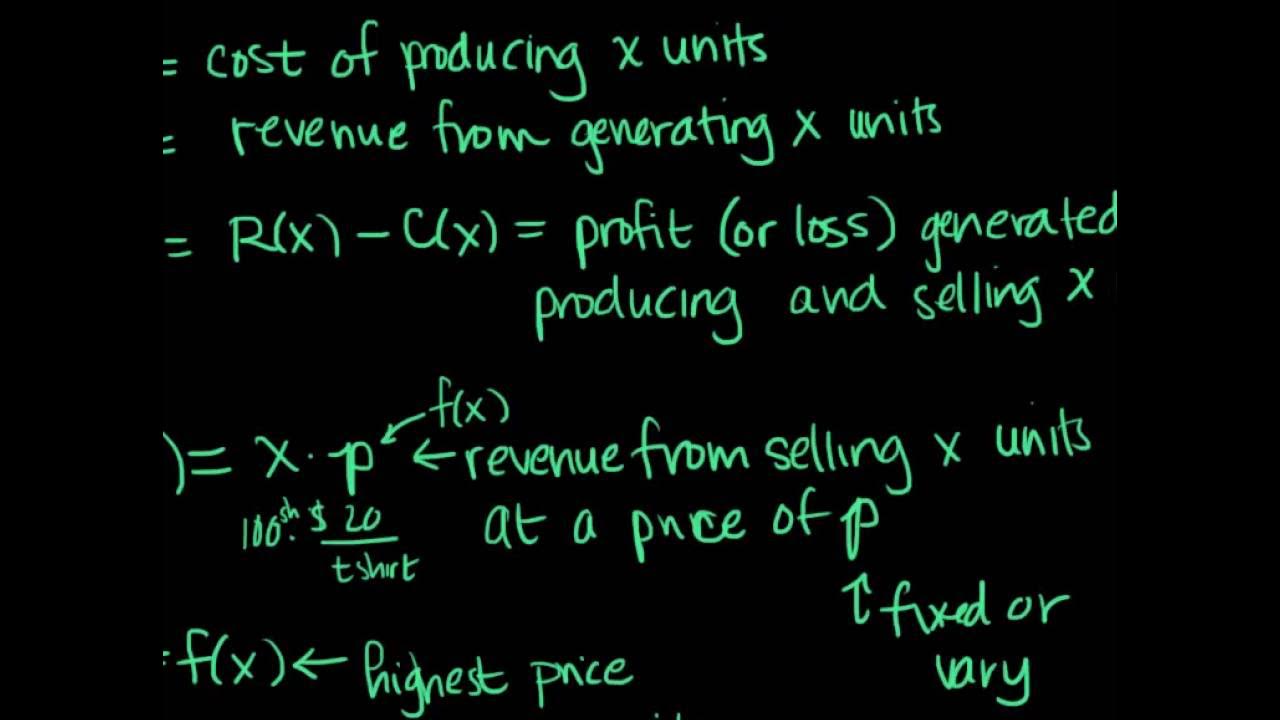BusCalc 10 Marginal Profit
TLDRThis video script presents a comprehensive example of applying calculus concepts, specifically derivatives, to a business scenario. The business in focus is Amanda's scented candle production and sale. The video covers the calculation of total cost, average cost per candle, and the concept of marginal cost, which is the derivative of the cost function. It then explores demand and revenue, introducing the marginal revenue as the derivative of the revenue function. Profit maximization is also discussed, highlighting the relationship between revenue, cost, and profit, and how to find the optimal number of candles to produce for maximum profit using derivatives. The script uses desmos.com for visual representation and emphasizes the importance of setting a price above the cost of production to ensure profitability. The video concludes with the maximum profit achieved by selling 854 candles at an optimal price of $11.46, resulting in a profit of $6862.
Takeaways
- 📈 The concept of marginal cost is introduced as the derivative of the cost function, which represents the cost of producing one additional unit.
- 📊 Marginal revenue is also defined as the derivative of the revenue function, indicating the additional revenue generated from selling one more unit.
- 💰 Profit is calculated as the difference between revenue and cost, and like revenue and cost, it is a function of the number of units sold.
- ✅ The average cost per unit can be found by dividing the total cost by the number of units produced.
- 🔢 The break-even point is the number of units that must be sold for the total revenue to equal the total cost, avoiding a loss.
- 📉 As the quantity of candles produced increases, the average cost per candle decreases due to economies of scale.
- 📚 The demand function describes how many candles will be sold at a given retail price, with higher prices generally leading to lower sales volumes.
- 🔍 The revenue function is derived from the product of the number of candles sold and the price per candle, which can be manipulated to express price as a function of quantity sold.
- 📉 The marginal revenue per candle is typically less than the price per candle because to sell an additional unit, the price often needs to be lowered, reducing the revenue gained from the additional sale.
- 🔧 To maximize profit, a business must set the price and quantity produced such that the price received for each unit sold is greater than the cost to produce that unit.
- 📝 Using tools like Desmos.com or by setting the derivative of the profit function to zero, one can determine the quantity of goods that will result in maximum profit.
Q & A
What is the total cost of production if Amanda plans to produce 20 candles?
-The total cost of production for 20 candles is calculated by evaluating the cost function at n = 20, which results in a cost of $211.
How is the average cost per candle calculated?
-The average cost per candle is determined by dividing the total cost of production by the number of candles produced. For 20 candles, the average cost is $10.55 per candle.
What does marginal cost represent in the context of Amanda's business?
-Marginal cost represents the cost of producing one additional unit of product (in this case, one more candle). It is calculated as the derivative of the cost function with respect to the number of candles produced.
What is the formula for marginal cost based on the provided transcript?
-The formula for marginal cost is C'(n) = 2 + 7 * n^(-0.3), where n is the number of candles.
How many candles would Amanda expect to sell if she sets the price at $5 per candle?
-According to the demand function, if Amanda sets the price at $5 per candle, she could expect to sell 1500 candles.
What is the relationship between the price per candle and the number of candles sold?
-As the price per candle increases, the number of candles sold decreases, indicating a negative correlation between price and quantity demanded.
How is revenue calculated for Amanda's candle business?
-Revenue is calculated by multiplying the number of candles sold (n) by the price per candle (p). Revenue is a function of the number of candles sold.
What is the total revenue if Amanda plans to sell 20 candles?
-The total revenue for selling 20 candles is $396, which is calculated using the revenue function with n = 20.
Why is the marginal revenue for selling one more candle typically less than the price per candle?
-The marginal revenue for selling one more candle is less than the price per candle because to sell an additional candle, the price typically needs to be lowered to incentivize the purchase, thus reducing the revenue gained from that sale.
What is the total profit if Amanda plans to produce and sell 20 candles?
-The total profit for selling 20 candles is $184.58, which is the difference between the total revenue and the total cost of production.
How can Amanda maximize her profit from selling candles?
-Amanda can maximize her profit by producing and selling 854 candles at a price of $11.46 each, as determined by the optimization of her profit function.
Outlines
📚 Introduction to Business Calculus
The video begins with an introduction to applying calculus concepts, specifically derivatives, to business scenarios. It discusses topics such as cost, marginal cost, demand, revenue, and marginal revenue in the context of Amanda's candle-making business. The script outlines the cost function, calculates total and average costs for producing 20 candles, and introduces the concept of marginal cost as the derivative of the cost function.
📊 Deriving Marginal Cost and Economies of Scale
The paragraph delves into the calculation of marginal cost, which is the cost of producing one additional unit. It explains the concept using the cost function and derives the marginal cost formula. It also discusses how marginal costs decrease with increased production due to economies of scale, providing a specific calculation for the marginal cost at 20 candles and highlighting the cost advantages of larger production batches.
🔢 Cost Analysis for Larger Production Batches
This section extends the cost analysis to larger production volumes, specifically 500 candles. It calculates the total cost, average cost per candle, and the cost to produce one additional candle at this volume. The discussion emphasizes the impact of economies of scale on reducing the average cost per candle and the marginal cost.
📈 Estimating Consumer Demand and Pricing Strategy
The focus shifts to consumer demand and how it relates to pricing. The demand function is introduced, and the script calculates expected sales volumes at different price points. It also addresses how to rearrange the demand function to express price as a function of the number of candles sold, which aids in determining the pricing strategy to achieve a target sales volume.
💰 Revenue, Average Revenue, and Marginal Revenue
Revenue is defined as the total money brought in by the business, calculated as the number of candles sold multiplied by the price per candle. The paragraph discusses how to calculate total revenue for selling a certain number of candles, average revenue per candle, and marginal revenue. It also explains that average revenue per candle equals the price per candle and derives the formula for marginal revenue.
📉 Understanding the Difference Between Average and Marginal Revenue
This section clarifies why average revenue per candle equals the price, whereas marginal revenue is not equal to the price. It discusses the relationship between price and demand and how lowering the price can increase demand. The script provides calculations for total revenue, average revenue, and marginal revenue when selling 500 candles.
🤑 Profit Analysis and Function Simplification
Profit is introduced as the difference between revenue and costs. The paragraph simplifies the profit function to make it easier to calculate profit for different numbers of candles produced and sold. It calculates the total profit for selling 20 candles and provides a formula for profit as a function of the number of candles.
📊 Average and Marginal Profit Calculations
The script calculates the average profit per candle for selling 20 candles and introduces the concept of marginal profit, which is the derivative of the profit function with respect to the number of candles. It provides a formula for marginal profit and calculates the profit for selling one more candle after producing and selling 20 candles.
🔍 Maximizing Profit Through Optimization
The final section addresses the optimization problem of finding the ideal number of candles to produce and sell to maximize profit. It uses Desmos.com to graph the profit function and identify the break-even point and the number of candles that yield the maximum profit. The paragraph concludes with the optimal number of candles to sell and the ideal pricing strategy to maximize profit.
🧮 Deriving the Maximum Profit Mathematically
The paragraph outlines a method to find the maximum profit without a graphing tool. It explains that the derivative of the profit function is zero at the point of maximum profit. The script shows how to set the derivative equal to zero and solve for the number of candles sold that would yield this maximum profit, highlighting the mathematical approach to optimization.
Mindmap
Keywords
💡Derivative
💡Cost Function
💡Marginal Cost
💡Demand Function
💡Revenue Function
💡Marginal Revenue
💡Profit Function
💡Average Cost
💡Break-Even Point
💡Optimization
💡Economies of Scale
Highlights
The video discusses applying calculus concepts, specifically derivatives, to a business scenario involving cost, revenue, and profit analysis.
Marginal cost is introduced as the derivative of the cost function, which represents the cost to produce one additional unit.
The concept of economies of scale is explained through the decreasing nature of the marginal cost as the number of produced units increases.
The average cost per unit is calculated by dividing the total cost by the number of units produced.
The relationship between price, demand, and revenue is explored, with revenue being the product of the number of units sold and the price per unit.
The derivative of the revenue function with respect to the number of candles sold is defined as marginal revenue.
Profit is defined as the difference between revenue and cost, and the video shows how to calculate total, average, and marginal profit.
The video uses a real-world example of a candle-making business to illustrate the application of these concepts.
The importance of pricing strategy in maximizing profit is discussed, with the price function derived from the demand function.
The concept of the break-even point is introduced, where the total cost equals the total revenue, resulting in zero profit.
The video demonstrates how to use Desmos.com to graph the profit function and find the number of units that maximize profit.
The mathematical optimization problem is solved to find the ideal number of candles to produce and sell for maximum profit.
The video concludes with the strategy that a business should price its product above the cost of production to ensure profitability.
The use of calculus in business for decision-making is emphasized, highlighting its practical applications in areas like pricing and production.
The video provides a comprehensive look at how derivatives can be used to find maximum profit in a business context.
The process of calculating total, average, and marginal values for cost, revenue, and profit is demonstrated step-by-step.
The relationship between marginal revenue, price, and quantity sold is explored, showing why marginal revenue is often less than the price per unit.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: