Simulation providing evidence that (n-1) gives us unbiased estimate | Khan Academy

Khan Academy
26 Nov 201204:29
EducationalLearning
32 Likes 10 Comments

TLDRThe video script from Khan Academy user TETF introduces an interactive simulation that illustrates the rationale behind using n-1 (where n is the sample size) in the calculation of sample variance to achieve an unbiased estimate of the population variance. The simulation allows users to construct a population by clicking in a blue area, from which they can then randomly select samples of varying sizes. For each sample, the simulation calculates the variance using different denominators ranging from n-3 to n+a, and then averages these variances to find the best estimate. The key insight is that the most accurate estimate of the population variance is obtained when the denominator is n-1, which is slightly less than the sample size. This method avoids both underestimating and overestimating the true population variance. The script encourages viewers to engage with the simulation to gain a deeper understanding of statistical concepts.

Takeaways
  • 📐 The simulation by TETF (pronounced tet f) from Khan Academy illustrates the rationale behind using n-1 in sample variance calculations.
  • 🌟 By constructing a population through random clicks, the simulation allows users to create their own dataset and observe statistical parameters.
  • 📈 The population mean and standard deviation, derived from the population variance, are calculated and displayed during the simulation.
  • 🔍 The simulation demonstrates taking samples of various sizes and calculating the variance for each, offering insight into statistical sampling.
  • 🔢 The process involves squaring the difference between each data point and the sample mean, then dividing by n plus a variable (a).
  • 📊 The simulation explores different values of 'a' to find the best estimate for the population variance, ranging from n-3 to n+a.
  • 🧮 It shows that using n-1 (or a close negative value) as the divisor results in the most accurate estimate of the population variance.
  • 📉 For values of 'a' greater than -1, the simulation indicates an underestimation of the population variance.
  • 📈 Conversely, for values of 'a' less than -1, the population variance is overestimated.
  • 🔁 The simulation emphasizes the importance of averaging the results from many samples to find the most unbiased estimate.
  • 🔍 The best estimate consistently approaches n-1, regardless of the sample size, reinforcing the statistical principle for variance calculation.
Q & A

  • What does the simulation created by TETF on Khan Academy allow users to understand?

    -The simulation allows users to gain an intuition as to why we divide by n minus 1 when calculating sample variance and why that gives us an unbiased estimate of the population variance.

  • How is the population created in the simulation?

    -The population is created by clicking in the blue area, which increases the population size with each click.

  • What parameters does the simulation calculate for the population?

    -The simulation calculates the population mean, standard deviation, and population variance.

  • What is the relationship between the population standard deviation and variance?

    -The population variance is the square of the population standard deviation.

  • How does the simulation determine the best estimate for the population variance?

    -The simulation takes the mean of the variances calculated for different values of 'a' (ranging from n minus 3 to n plus a) across many samples to determine the best estimate.

  • What does the simulation show about the value of 'a' that provides the best estimate of the population variance?

    -The best estimate is found when 'a' is close to negative 1, which corresponds to dividing by n minus 1.

  • What happens when 'a' is less than negative 1 in the simulation?

    -When 'a' is less than negative 1, the simulation starts overestimating the population variance.

  • What happens when 'a' is greater than negative 1 in the simulation?

    -When 'a' is greater than negative 1, the simulation starts underestimating the population variance.

  • Can the simulation be used for samples of different sizes?

    -Yes, the simulation can be used for samples of different sizes to determine the best estimate for the population variance.

  • What is the significance of generating a large number of samples in the simulation?

    -Generating a large number of samples helps to refine the estimate and shows that the best estimate is when 'a' is negative 1, especially as the number of samples approaches millions.

  • Who is credited for creating the simulation discussed in the script?

    -TETF, pronounced as 'tet f', is credited for creating the simulation.

  • What is the purpose of the simulation in the context of statistical learning?

    -The simulation serves as an educational tool to help understand the concept of unbiased estimation of population variance through the process of sample variance calculation.

Outlines
00:00
📊 Understanding Sample Variance Calculation

The video script introduces a simulation by a Khan Academy user, TETF, which helps in understanding the rationale behind dividing by n-1 when calculating sample variance to obtain an unbiased estimate of the population variance. The simulation allows users to create a population by clicking in a blue area, which increases the population size with each click. The population's parameters, including the mean and standard deviation, are calculated and displayed. The key insight is provided by taking samples of various sizes and calculating the variance for each sample, adjusting the divisor from n-3 to n+a. The simulation shows that the best estimate for population variance is achieved when the divisor is n-1, providing an unbiased estimate. This is demonstrated through multiple samples and averaging the results.

Mindmap
Keywords
💡Sample Variance
Sample variance is a measure of how much the values in a sample differ from the mean of that sample. It is calculated by taking the sum of the squared differences between each data point and the sample mean, then dividing by the sample size minus one. In the video, it is discussed why dividing by n-1 (n being the sample size) gives an unbiased estimate of the population variance.
💡Unbiased Estimate
An unbiased estimate is a statistical measure that does not systematically overestimate or underestimate the true value of a parameter. In the context of the video, it refers to the use of n-1 in the variance calculation to ensure that the sample variance provides an unbiased estimate of the population variance.
💡Population Mean
The population mean is the average value of a population, calculated by dividing the sum of all the values in the population by the number of values. In the video, the population mean is calculated as 204.09, and it serves as a reference point for calculating the sample variance.
💡Population Variance
Population variance is a measure of the dispersion of all the values in a population. It is calculated by taking the average of the squared differences between each value in the population and the population mean. In the video, the population variance is derived from the standard deviation squared, which is 63.8 squared.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It is the square root of the variance and indicates the average distance of each value from the mean. In the video, the population standard deviation is 63.8, which is used to calculate the population variance.
💡Simulation
A simulation is a method of modeling the operation of a real-world process or system. In this video, a simulation created by a Khan Academy user is used to demonstrate the concept of sample variance and why dividing by n-1 is necessary for an unbiased estimate. The simulation allows users to construct a population and take samples to observe the calculation of variance.
💡Sample Size
Sample size refers to the number of observations or data points collected in a sample. In the video, the sample size is varied to demonstrate how it affects the calculation of sample variance and the resulting estimate of the population variance.
💡Sum of Squared Differences
The sum of squared differences is the sum of the squared differences between each data point in a sample and the sample mean. This is a key component in the calculation of variance, as it measures the dispersion of the sample data. In the video, this sum is used in the formula for calculating sample variance.
💡Dividing by n-1
Dividing by n-1 is a common practice in statistics when calculating the sample variance. This is done to correct for the bias in the estimation of the population variance from a sample. The video explains through a simulation that dividing by n-1, rather than n, provides an unbiased estimate of the population variance.
💡Mean of Variances
The mean of variances is the average of the variances calculated from multiple samples. In the video, the mean of variances is taken across different values of 'a' (where the variance is calculated as the sum of squared differences divided by n plus a) to determine which value of 'a' provides the best estimate of the population variance.
💡Khan Academy
Khan Academy is a non-profit educational organization that provides free online courses, lessons, and practice exercises in a variety of subjects, including math and computer science. In the video, the simulation used to explain the concept of sample variance is created by a Khan Academy user and is available on the Khan Academy platform.
💡Computer Science
Computer science is the study of computers and computational systems, including their theory, design, development, and application. In the context of the video, the simulation that demonstrates the concept of sample variance is a part of the computer science offerings on the Khan Academy website, where users can interact with the simulation to gain a deeper understanding of statistical concepts.
Highlights

Simulation created by Khan Academy user TETF allows for an intuitive understanding of why we divide by n-1 in sample variance calculation.

The simulation enables users to construct a population by clicking in a blue area, increasing the population size with each click.

The population mean and standard deviation are calculated and displayed during the population construction process.

Population variance is derived from the standard deviation and displayed as the squared value of the standard deviation.

The simulation demonstrates the process of taking samples from the population and calculating variance for each sample.

Variance is calculated by summing the squared differences between each data point and the sample mean, then dividing by n plus a varying value of 'a'.

The simulation explores different values of 'a' to find the best estimate for the population variance by averaging variances across numerous samples.

When 'a' is high, the simulation underestimates the population variance; when 'a' is low, it overestimates.

The optimal estimate for population variance is found when 'a' is close to -1, corresponding to dividing by n-1.

The simulation shows that dividing by n or n+0.05 results in underestimating the population variance.

Using n-1.05 or n-1.5 leads to overestimating the population variance.

The simulation can be repeated for samples of different sizes to validate the findings.

With a larger sample size of 6, the simulation consistently shows that dividing by n-1 provides the best estimate of population variance.

The simulation suggests that with millions of samples generated, the estimate using n-1 as the divisor would be the most accurate.

The simulation provides a practical application for understanding the statistical concept of unbiased estimation of population variance.

TETF's simulation is commended for its innovative approach to explaining a complex statistical concept in an accessible and visual manner.

The simulation encourages active participation by inviting users to construct their own populations and observe the effects on variance calculation.

The process of generating multiple samples and averaging their variances is key to understanding the unbiased estimate of population variance.

Transcripts

Browse More Related Video

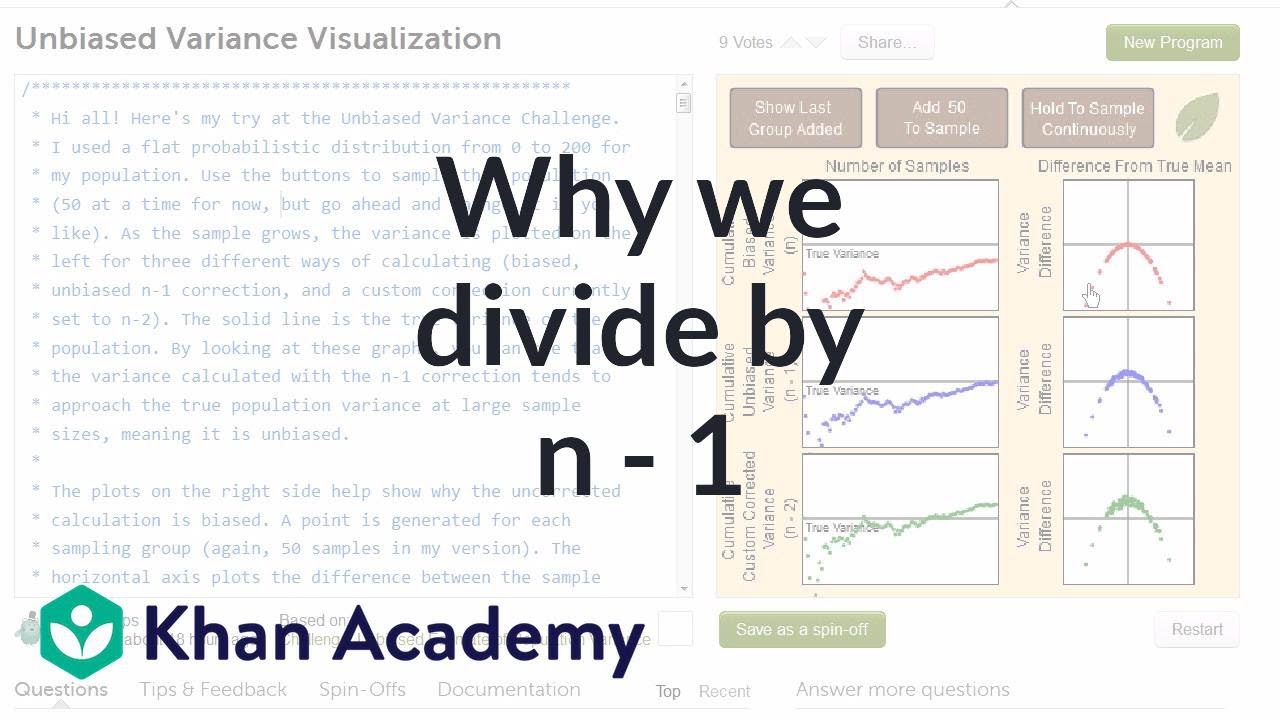
Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance

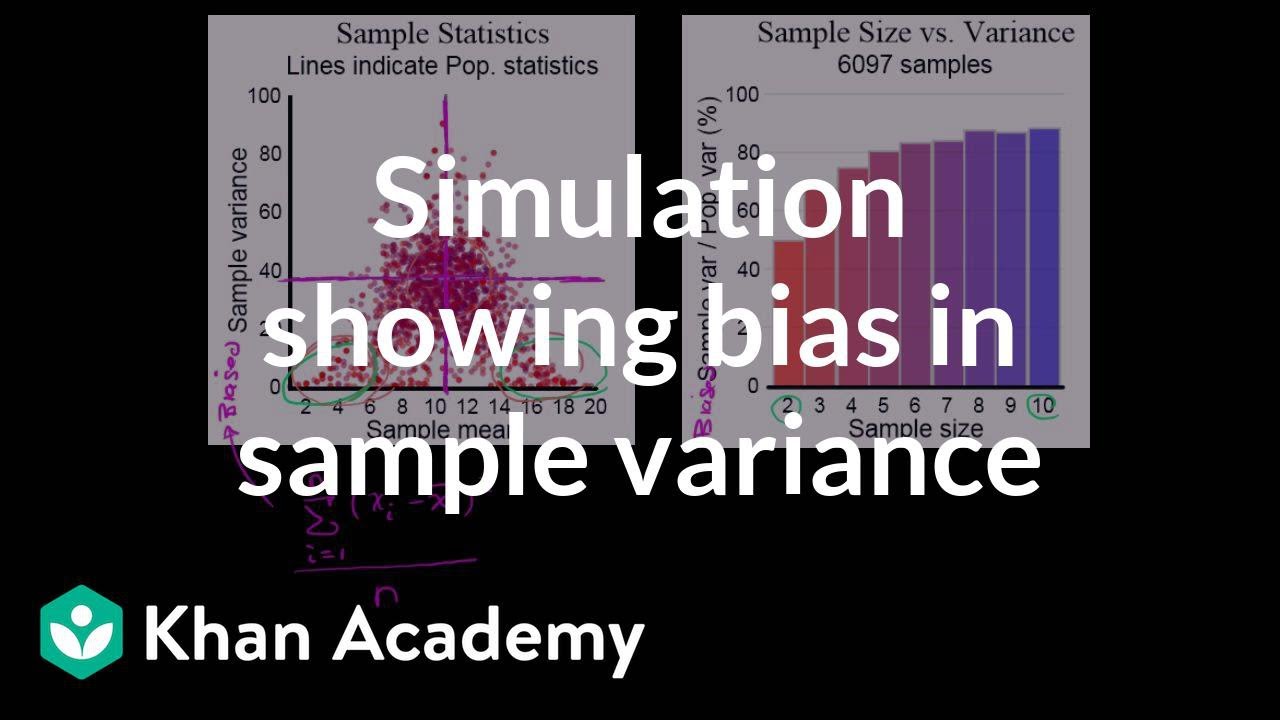
Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

Why do we divide by n-1 and not n? | shown with a simple example | variance and sd

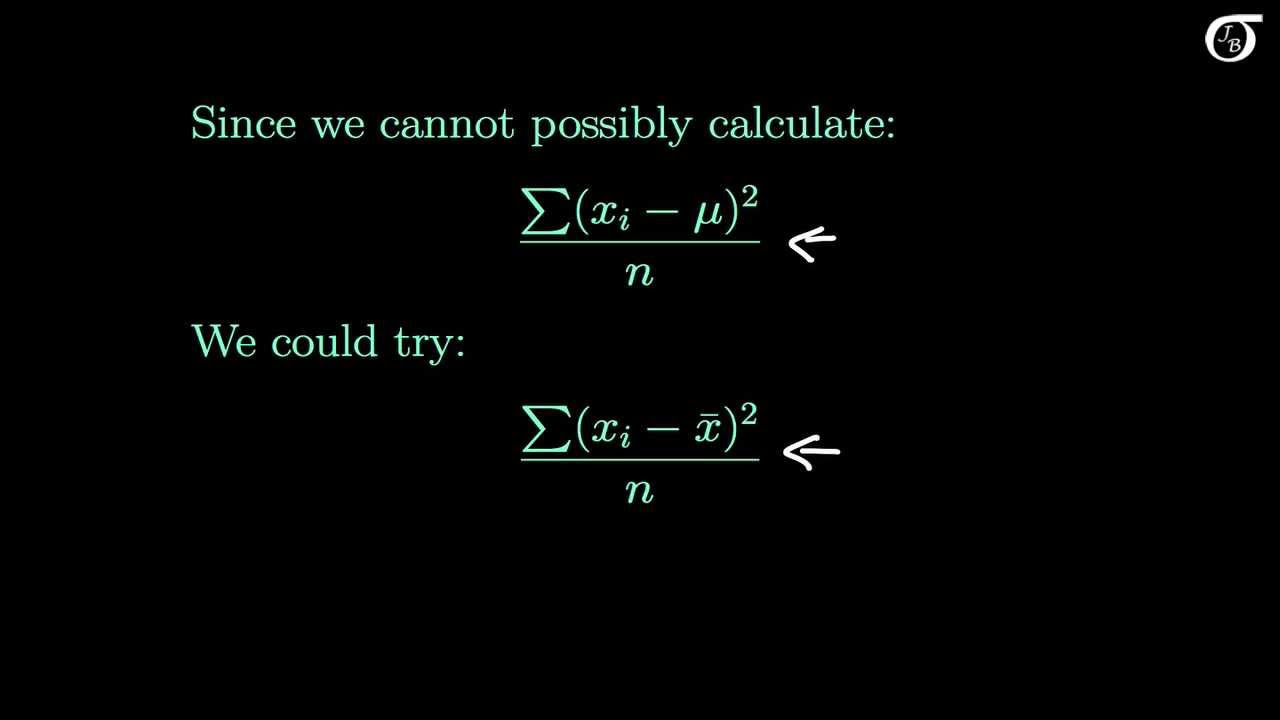
The Sample Variance: Why Divide by n-1?

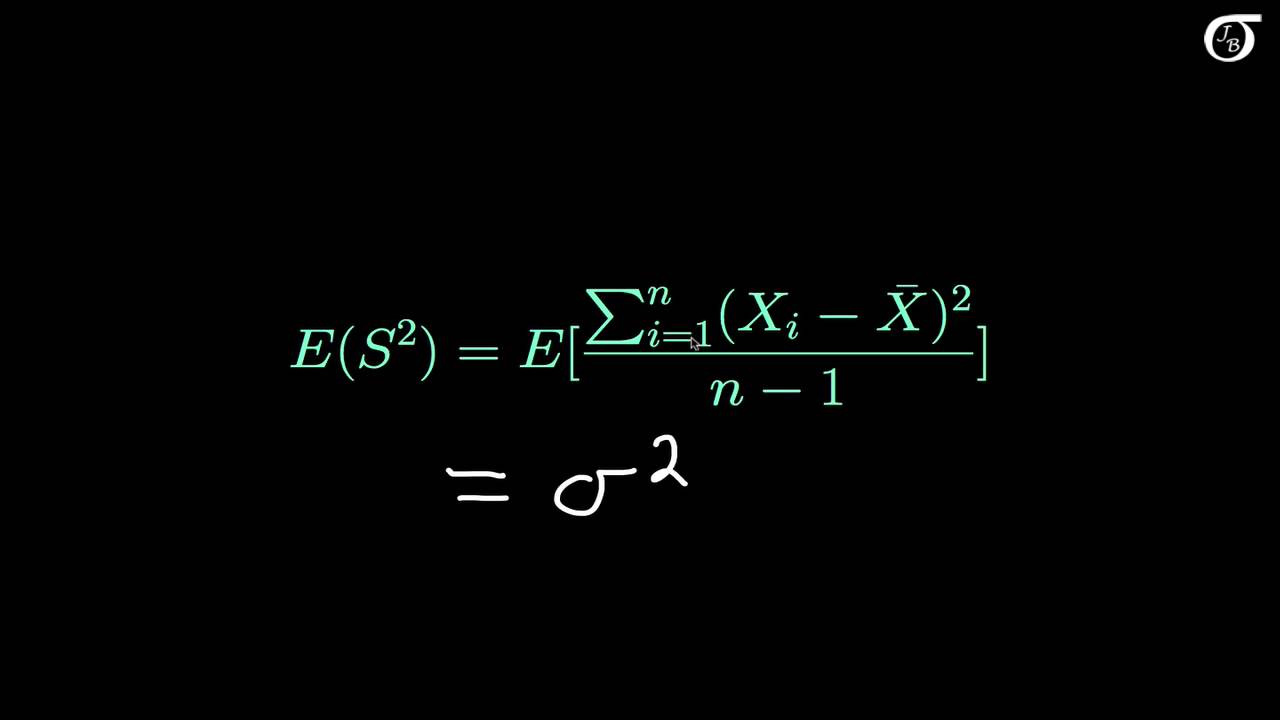
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance

Statistics: Sample variance | Descriptive statistics | Probability and Statistics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Sample VariancePopulation StatisticsKhan AcademySimulationTETFUnbiased EstimateStatistical IntuitionData AnalysisMath EducationVariance CalculationInteractive Learning