Elementary Stats Lesson #18
TLDRThis video script offers an in-depth tutorial on hypothesis testing for population proportions, covering two primary methods: the p-value approach and the classical critical value method. It explains the process of setting up hypotheses, selecting significance levels, calculating test statistics, and making decisions based on p-values or critical regions. The script uses various examples to illustrate right-tailed, left-tailed, and two-tailed tests, emphasizing the importance of understanding the p-value and the conditions required for hypothesis testing.
Takeaways
- 📚 The lesson focuses on hypothesis testing for population proportions, introducing two methods: the p-value approach and the classical critical value method.
- 🔍 The p-value approach involves calculating a test statistic (z-score) and comparing it to a probability (p-value) derived from the normal distribution.
- 📉 For a right-tailed test, the p-value represents the probability of obtaining a sample result as extreme or more extreme than the observed sample, assuming the null hypothesis is true.
- 📈 The classical method turns the significance level (alpha) into a critical value on the z-distribution and compares the test statistic to this value to decide whether to reject the null hypothesis.
- ⚖️ Both methods require checking certain conditions before conducting the test, such as simple random sampling, a sufficiently large sample size, and independence of sample values.
- 📝 The script provides step-by-step instructions for setting up hypothesis tests, including determining null and alternative hypotheses, selecting a significance level, calculating the test statistic, and making a decision based on the p-value or critical value.
- 📊 Examples are given to illustrate the process of hypothesis testing, including how to calculate the test statistic and p-value, and how to interpret the results to reach a conclusion.
- 🔢 The script mentions the use of calculator programs to assist with the calculations involved in hypothesis testing, which can simplify the process and reduce the potential for errors.
- 📉 In a right-tailed test, if the p-value is less than the significance level (alpha), the null hypothesis is rejected in favor of the alternative hypothesis.
- 📊 For a two-tailed test, the p-value is calculated as the sum of the probabilities in both tails, and the test statistic must be compared to both critical values to determine the decision.
- 🔑 The script emphasizes the importance of understanding the meaning of p-values and critical values in hypothesis testing and how they guide the decision-making process.
Q & A
What is the main topic of the video script?
-The main topic of the video script is hypothesis testing for population proportions, including the use of p-value and critical value methods.
What are the two primary methods for conducting hypothesis tests discussed in the script?
-The two primary methods for conducting hypothesis tests discussed in the script are the p-value approach and the classical critical value method.
What is the purpose of the null hypothesis in a hypothesis test?
-The null hypothesis serves as the default assumption that there is no effect or no difference; it is assumed to be true until evidence suggests otherwise.
What is the significance level (alpha) in a hypothesis test, and why is it important?
-The significance level (alpha) is the threshold for deciding when to reject the null hypothesis; it represents the probability of making a Type I error and is important for determining the strength of evidence needed to reject the null hypothesis.
How is the test statistic calculated in a hypothesis test for a population proportion?
-The test statistic is calculated by taking the sample proportion, subtracting the null hypothesis proportion, and dividing by the standard error, which is the square root of (p * (1 - p)) / n, where p is the null proportion and n is the sample size.
What is a p-value in the context of hypothesis testing?
-A p-value is the probability of obtaining a test statistic as extreme or more extreme than the one calculated from the sample, assuming the null hypothesis is true. It is used to determine whether there is sufficient evidence to reject the null hypothesis.
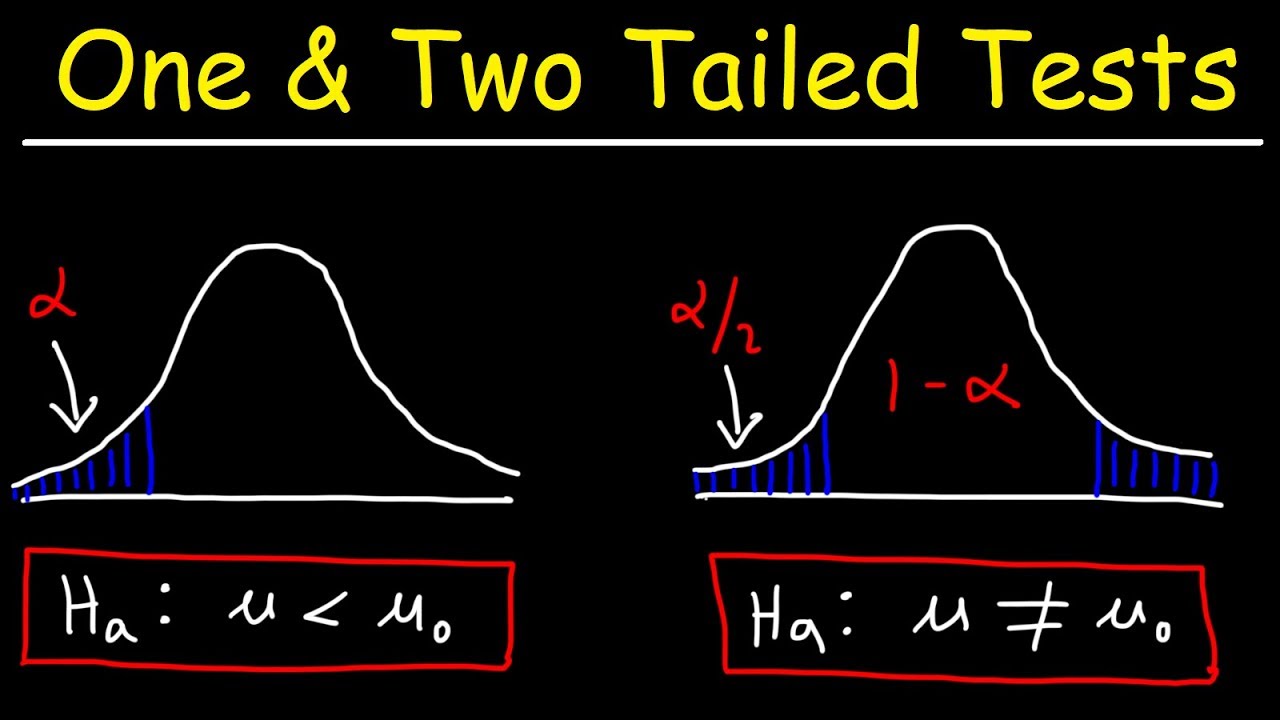
What is the difference between a one-tailed and a two-tailed test in hypothesis testing?
-A one-tailed test focuses on one direction (either greater than or less than the null hypothesis value), while a two-tailed test considers both directions, testing for a difference from the null hypothesis in either direction.
How does the sample size affect the hypothesis test for a population proportion?
-The sample size affects the hypothesis test by determining the standard error of the proportion. A larger sample size generally provides a more accurate estimate and a more reliable test statistic.
What are the conditions that need to be met before conducting a hypothesis test for a population proportion?
-The conditions that need to be met include simple random sampling, a large enough sample size (n * p * (1 - p) should be at least 10), and the sample values being independent of one another (sample size is less than 5% of the population size).
Can you provide an example of how to use a calculator to perform a one proportion z-test?
-To use a calculator for a one proportion z-test, you would enter the null proportion, the number of successes, and the sample size. Then, you would select the appropriate alternative hypothesis (greater than, less than, or not equal to) and calculate the test statistic and p-value.
Outlines
📚 Introduction to Hypothesis Testing for Population Proportions
The video begins with an introduction to hypothesis testing, specifically focusing on population proportions. The instructor outlines the structure of the lesson, which includes hypothesis testing for a single population proportion using section 10.2 of the course material. The simplicity of proportions as variables is highlighted, and a template for hypothesis testing is presented, along with new terminology such as 'sample proportion' and 'p-hat'. The example of testing public opinion on banning cell phone use while driving is used to illustrate the process, with a sample size of a thousand and a sample proportion of 0.534, leading to the question of whether the true population proportion is greater than 0.50.
🔍 Setting Up Hypothesis Tests and Calculating Test Statistics
The instructor continues by detailing the steps involved in setting up a hypothesis test, emphasizing the importance of the null hypothesis as the assumed truth. The significance level (alpha) is introduced as the threshold for making a decision in the hypothesis test. The process of calculating the test statistic is explained, using the sample proportion and the standard error to create a standardized z-score. The example from the first paragraph is revisited to demonstrate the calculation of the test statistic, resulting in a z-score of 2.15, indicating a sample result that is 2.15 standard units away from the null hypothesis.
📉 Understanding P-Values and Making Decisions in Hypothesis Testing
The concept of p-values is introduced as the probability of obtaining a sample result as extreme or more extreme than the one observed, assuming the null hypothesis is true. The instructor explains the importance of p-values in hypothesis testing and demonstrates how they are used to make a decision by comparing them to the significance level. Using the example from the first paragraph, a p-value of 0.0158 is calculated, which is less than the alpha level of 0.05, leading to the rejection of the null hypothesis in favor of the alternate hypothesis that the true population proportion is greater than 0.50.
📈 Hypothesis Testing Examples and Calculator Assistance
The instructor presents additional examples of hypothesis testing, including scenarios where the null hypothesis is tested for no change in public trust in media over time and where the proportion of Americans distrusting the media is evaluated for an increase. The use of a calculator to assist with the calculations in hypothesis testing is introduced, specifically for a one-proportion z-test, demonstrating how to input the null proportion, sample successes, and sample size to obtain the test statistic and p-value.
📉 Left-Tailed, Right-Tailed, and Two-Tailed Tests
The video script covers different types of hypothesis tests, including left-tailed, right-tailed, and two-tailed tests. The instructor explains the conditions for each test type and how to calculate the test statistic and p-value accordingly. Examples are provided for each test type, illustrating how to set up the hypothesis, calculate the test statistic, determine the p-value, and make a decision based on the comparison of the p-value to the significance level.
🔢 Critical Value Method for Hypothesis Testing
An alternative method for hypothesis testing, known as the critical value method, is introduced. The instructor explains how to determine the critical value based on the significance level and compares it to the test statistic to make a decision. The method is demonstrated with an example where the president of a company wants to test if more than 50% of employees are satisfied with their jobs, using a sample of 100 employees with 54 expressing satisfaction.
📉 Applying the Critical Value Method to Hypothesis Testing
The instructor provides a detailed explanation of how to apply the critical value method to hypothesis testing, including the steps for setting up the test, computing the test statistic, determining the critical value, and making a decision based on whether the test statistic falls within the critical region. Examples of right-tailed and two-tailed tests are given to illustrate the process, emphasizing the importance of understanding the logic behind the method.
📊 Conclusion of Hypothesis Testing for Population Proportions
The video concludes with a summary of the hypothesis testing process for population proportions, highlighting the two methods discussed: the p-value method and the critical value method. The instructor emphasizes that both methods will lead to the same conclusion and that the steps for testing hypotheses about population means will be similar, with adjustments for the t-distribution in the next lessons.
Mindmap
Keywords
💡Hypothesis Test
💡Population Proportion
💡Sample Proportion (p-hat)
💡Null Hypothesis (H0)
💡Alternate Hypothesis (H1)
💡Significance Level (Alpha)
💡Test Statistic
💡P-value
💡Critical Value
💡Z-score
💡Type I Error
💡Normal Distribution
💡Simple Random Sampling
Highlights
Introduction to hypothesis tests for population proportions with a focus on simplicity and ease of use compared to tests for means.
Explanation of a complete template for hypothesis tests of a single population proportion.
Discussion of the conditions required for hypothesis testing, including simple random sampling and sample size conditions.
Description of the five-step process for hypothesis testing, from setting up hypotheses to making a decision.
Emphasis on the importance of the null hypothesis as the assumed value until evidence suggests otherwise.
Introduction of the p-value approach as the primary method for hypothesis testing.
Explanation of the test statistic as a standardized version of the sample result under the null hypothesis.
Clarification of the p-value as the probability of obtaining a sample result as extreme as the observed, assuming the null hypothesis is true.
Demonstration of calculating the test statistic and p-value for a sample proportion indicating support for a policy.
Use of a calculator program to assist with hypothesis test calculations, streamlining the process.
Presentation of an example involving trust in media and the application of a hypothesis test to determine if trust has changed over time.
Introduction of the classical method or critical value method as an alternative to the p-value approach.
Explanation of the critical value method, which involves comparing the test statistic to critical z-scores rather than probabilities.
Illustration of the critical region concept in hypothesis testing and its role in decision-making.
Comparison of the p-value and classical methods, highlighting their equivalence in reaching conclusions.
Discussion of the implications of hypothesis testing for practical applications, such as determining employee satisfaction.
Final remarks on the importance of hypothesis testing in statistical analysis and its application in the next lessons for population means.
Transcripts
Browse More Related Video

9.1.3 Two Proportions - Example, Critical Value Method, Normal Approximation

8.1.5 Basics of Hypothesis Testing - P-value Method, and Comparison to the Critical Value Method

Hypothesis testing: step-by-step, p-value, t-test for difference of two means - Statistics Help
One Tailed and Two Tailed Tests, Critical Values, & Significance Level - Inferential Statistics

Elementary Statistics - Chapter 8 - Hypothesis Testing Part 3 Revised

Elementary Statistics Chapter 8 - Introduction Hypothesis Testing Part 1 Lesson 1
5.0 / 5 (0 votes)
Thanks for rating: