Fundamental Theorem of Calculus FRQs
TLDRThe video script presents an in-depth exploration of the Fundamental Theorem of Calculus (FTC), emphasizing its significance in understanding the relationship between integrals and derivatives. The speaker anticipates that FTC problems will feature prominently in the upcoming AP test, and thus, provides a comprehensive guide to tackling these complex mathematical challenges. The script walks viewers through various FTC problems, starting with a piecewise function and its integral, leading to the calculation of G of 8, G prime of 8, and G double prime of 8. It then delves into function analysis, examining the existence of relative maxima and minima, and identifying points of inflection. The script also covers the application of FTC to calculate derivatives and integrals symbolically, using the graphs of functions like F or G prime. Absolute maxima and minima are discussed, with a focus on identifying critical points and endpoints to determine these values. The video concludes with a twist on a 2017 AP test problem, illustrating the use of u-substitution and the reverse chain rule in calculating integrals. Throughout, the emphasis is on conceptual understanding rather than rote memorization, encouraging viewers to engage with the material critically.
Takeaways
- 📚 The video focuses on the Fundamental Theorem of Calculus (FTC), integrals, derivatives, and their interrelations, which are expected to be on the AP test.
- 🔗 The theme for FTC problems is to be aware of the given information and determine what information is needed to find the solution.
- 🧩 FTC problems are likened to puzzles that require thinking about what is given and what needs to be found, rather than a purely formulaic approach.
- 📈 G(x) is defined as an integral from 'a' to 'x', and G'(x) is the derivative of G(x), which is equal to the function being integrated, f(x).
- 📉 G''(x), the second derivative of G(x), can be found by taking the derivative of G'(x), which is f'(x), the derivative of the original function.
- 🤔 The existence of G''(x) can be determined by analyzing the graph of f(x) for points where the derivative is undefined, such as cusps.
- 📌 To find relative maxima or minima, look for changes in the sign of G'(x), while points of inflection in G(x) are determined by changes in the sign of G''(x).
- ✅ For AP test preparation, practice problems involving functions like e^(2x) times G(x), where symbolic and abstract understanding is crucial.
- 🚫 Avoid relying on photomath or googling for solutions; understand the concepts of integrals and derivatives to solve abstract calculus problems.
- 🔢 To find absolute maxima and minima, test endpoints and critical points of the interval, using the graph of G'(x) to determine where it changes sign.
- 🔃 When moving from F'(x) to F(x), use integrals and the Fundamental Theorem of Calculus to find the original function given its derivative.
- 💡 U-substitution is a useful technique for integrating more complex functions, such as when dealing with expressions like F''(3x).
Q & A
What is the main topic of the video?
-The main topic of the video is the Fundamental Theorem of Calculus (FTC), its problems, and the relationship between integrals and derivatives.
What does the speaker expect to be a significant part of the year's AP test?
-The speaker expects problems related to the Fundamental Theorem of Calculus, involving integrals and derivatives, to be a significant part of the year's AP test.
How does the speaker describe the approach to solving FTC problems?
-The speaker emphasizes the importance of understanding the given information, determining what needs to be found, and thinking critically about the relationship between integrals and derivatives rather than relying on a formulaic approach.
What is the significance of the graph in the first problem discussed in the video?
-The graph in the first problem is significant because it helps visualize the integral from 2 to 8 of the function F(t), allowing the calculation of the area under the curve to find the value of G(8).
How does the speaker explain the relationship between G'(x) and F(x)?
-The speaker explains that G'(x), the derivative of G, is equal to F(x) because derivatives and integrals have an inverse relationship that 'undoes' each other.
What is the significance of the cusp in the graph at x=8 in the first problem?
-The cusp at x=8 signifies that G''(x), the second derivative of G, does not exist at that point, which is an important consideration when analyzing the behavior of the function.
How does the speaker approach the problem of finding absolute maximum and minimum values in the context of FTC?
-The speaker approaches the problem by identifying critical points where G'(x) is zero or undefined, as well as the endpoints of the interval. Then, by plugging these points into the function G(x), the speaker calculates the function's values to determine the absolute maximum and minimum.
What is the method used to find F(x) when only the graph of F'(x) is given?
-The method used is based on the Fundamental Theorem of Calculus, which states that the integral of F'(x) from a to x gives F(x). The speaker sets up integrals with the given F'(x) over the appropriate intervals and uses the given F(-2) value to find F(x) at other points.
How does the speaker calculate the integral from -4 to 0 of F''(x)?
-The speaker uses the concept of antiderivatives and u-substitution. By setting u = 3x, the speaker rewrites the integral as 1/3 times the integral of F''(u) from u = -12 to u = 0, and then evaluates this using the graph of F'(x).
What is the key takeaway from the video regarding FTC problems?
-The key takeaway is that solving FTC problems requires a deep understanding of the concepts of integrals and derivatives, their relationship, and how they can be used to find solutions. It's not just about applying formulas but also about thinking critically and understanding the underlying mathematical principles.
Outlines
📚 Introduction to FTC Problems and Expectations
The speaker begins by introducing the topic of the video, which is the Fundamental Theorem of Calculus (FTC) and its application to problems involving integrals and derivatives. They express anticipation that these types of problems will feature prominently on the upcoming AP test. The emphasis is on understanding the relationship between the two mathematical concepts and being aware of the information given versus what needs to be found. The theme is set for the session, which is to approach problems as puzzles that require analytical thinking rather than formulaic application.
🔍 Analyzing Piecewise Functions and Derivatives
The video continues with an exploration of piecewise functions and their relationship to integrals and derivatives. The speaker uses a problem from 2016 as a framework but modifies it to demonstrate how to approach FTC problems. They discuss finding the value of a function G at a specific point by integrating from a lower bound to that point, effectively calculating the area under the curve of a piecewise function. The speaker also covers how to find the first and second derivatives of G, linking them back to the original function F, and addresses scenarios where the second derivative might not exist due to features like cusps in the graph.
📉 Function Analysis and Points of Inflection
The focus shifts to function analysis, specifically examining the behavior of functions at certain points. The speaker works through parts A and B of a problem set, using the graph of a piecewise linear function to determine whether there are relative maxima or minima at specific points. They also explore the concept of points of inflection, where the concavity of the function changes. The speaker emphasizes the importance of understanding changes in the sign of the first and second derivatives as indicators of these points.
🧮 Calculations Using Function Graphs
This section delves into using the graphs of functions to perform calculations, including finding integrals and derivatives. The speaker presents a modified problem from the 2016 model, illustrating how to calculate the derivative of a product of functions and how to integrate within a given interval. They highlight the importance of understanding the underlying mathematical concepts to solve these problems, as opposed to relying on tools that provide direct answers.
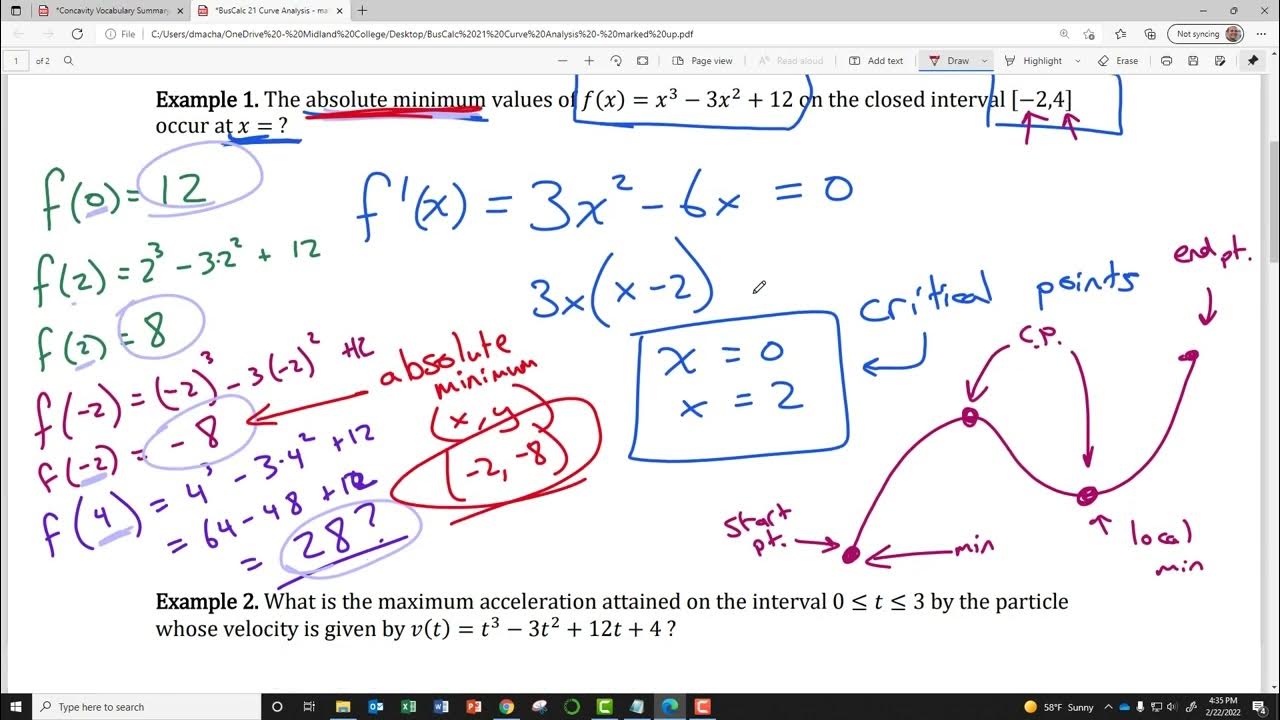
🔢 Finding Absolute Extrema Using FTC
The speaker introduces the concept of absolute maxima and minima within a closed interval, explaining how to identify these points on a graph. They guide viewers through creating a chart to test different candidates for absolute extrema by evaluating the function at endpoints and critical points. Using the FTC, they demonstrate how to calculate the function's value at various points and compare them to find the absolute maximum and minimum values.
🔁 Working Backwards from Derivatives to Functions
The video addresses a unique problem where the graph of the derivative of a function is given, and the task is to find the value of the original function at specific points. The speaker explains how to use the FTC to work backwards from the derivative to find the function's values. They provide a step-by-step method for setting up integrals that leverage the given information and the graph of the derivative to find the required function values.
🧐 Advanced FTC Problems and U-Substitution
The final section tackles more complex FTC problems, including those involving the antiderivative of a function multiplied by a variable. The speaker uses a twist on a problem from the 2017 exam to illustrate the use of u-substitution in integration. They show how to reverse-engineer an integral back to its original function and emphasize the importance of understanding the conceptual underpinnings of calculus to solve these problems successfully.
📝 Conclusion and Encouragement for FTC Problem Solving
In conclusion, the speaker reiterates the importance of starting with known information and linking it to what needs to be found when tackling FTC problems. They discourage a formulaic approach, instead encouraging viewers to think deeply about the meanings of integrals and derivatives and how these concepts can guide them to the solutions. The speaker wishes everyone a great day and concludes the video.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Integrals
💡Derivatives
💡AP Test
💡Piecewise Function
💡Absolute Maximum and Minimum
💡Chain Rule
💡Product Rule
💡U-Substitution
💡Points of Inflection
💡Critical Points
Highlights
The importance of understanding the Fundamental Theorem of Calculus and its application to problems involving integrals and derivatives is emphasized.
Expectation of encountering a variety of calculus problems on the AP test, particularly those related to the Fundamental Theorem of Calculus.
The necessity to be aware of given information and the required findings when approaching calculus problems, treating them more like puzzles.
An illustrative example is provided using a piecewise function to demonstrate how to find G of 8, G prime of 8, and G double prime of 8.
The concept that G prime of X is equal to the function f of X, highlighting the inverse relationship between derivatives and integrals.
The method to determine if G has a relative maximum or minimum at a specific point by analyzing the sign changes of G prime.
Explanation on how to identify points of inflection in the graph of G by examining the behavior of G prime.
The use of the product rule to find the derivative of a function H of X, which is a product of e to the 2x and G of X.
A demonstration of calculating H prime of 0 by substituting values into the derived expression of H prime of X.
The process of anti-deriving to find the integral from negative 4 to 0 of F prime of X, given the graph of F prime.
An overview of how to calculate absolute maxima and minima for a function defined by an integral, using a chart to test different candidates.
The application of the Fundamental Theorem of Calculus to find the values of F at specific points when given the graph of F prime.
An example of using u-substitution to calculate the integral of a function involving F double prime of 3X.
Emphasis on the need to understand integrals and derivatives symbolically and abstractly to solve complex calculus problems.
The reminder that problems involving absolute maxima and minima, as well as those from the Fundamental Theorem of Calculus, are expected to appear on the AP test.
A twist problem involving the calculation of an integral from negative to zero of F double prime of 3X, showcasing the use of u-substitution.
The final integral calculation resulting in 1/3 times negative 4, demonstrating the process of anti-deriving and substituting back into the original variable.
Advice to approach all calculus problems by starting with known information and linking it to what needs to be found, avoiding a purely formulaic mindset.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: