BusCalc 21 Curve Analysis
TLDRThis video script offers an in-depth exploration of curve analysis, focusing on the importance of understanding the behavior of functions through their derivatives. The presenter introduces a reference chart to help viewers memorize key concepts, such as the relationship between a function's value, its zeros, and its positivity or negativity. The script delves into the significance of critical points, where the first derivative is zero, and how these points can indicate local maxima, minima, or inflection points in a function's graph. The concept of concavity, determined by the second derivative, is also discussed, with attention given to how it can affect the shape of a function's curve. The presenter works through several example problems, demonstrating how to find absolute minimum and maximum values within a closed interval and how to analyze the maximum acceleration of a particle given its velocity function. The script concludes with a challenging problem involving finding a specific value for a parameter 'k' that results in a relative maximum for a given function. This comprehensive overview is designed to prepare viewers for an upcoming midterm exam, emphasizing the need to internalize these mathematical concepts for successful application.
Takeaways
- 📊 **Understanding Curve Analysis**: The video discusses curve analysis, focusing on how to interpret the behavior of a function based on its values and derivatives.
- ✅ **Function Values**: A function's value being less than zero indicates negative values, equal to zero signifies a zero of the function (x-intercept), and greater than zero means positive values.
- 📌 **Critical Points**: The first derivative equal to zero identifies critical points which can be relative maxima, minima, or inflection points.
- 📉 **Decreasing Function**: A first derivative less than zero means the function is decreasing, while a greater than zero value indicates the function is increasing.
- 🔽 **Concavity**: A second derivative less than zero suggests the function is concave down, equal to zero might indicate an inflection point, and greater than zero means the function is concave up.
- 🔍 **Inflection Points**: An inflection point is where the function changes concavity, from concave up to down or vice versa, and it occurs where the second derivative is zero.
- 🔢 **Absolute Extrema**: When finding absolute minimum or maximum values on a closed interval, evaluate the function at critical points and endpoints of the interval.
- 📘 **Memorization**: The reference chart provided in the video is meant to be memorized as it won't be available during an exam.
- 🔑 **Derivatives and Acceleration**: The derivative of velocity with respect to time gives acceleration, which is the focus for one of the example problems involving a particle's motion.
- 🔍 **Quotient Rule**: The video demonstrates the use of the quotient rule for finding derivatives, which is crucial for analyzing functions like natural logarithm divided by x.
- 📐 **Second Derivative Test**: The second derivative test is used to determine the concavity of a function, which helps in finding relative extrema.
- 🤔 **Problem Solving**: The script walks through several problems, emphasizing the process of finding derivatives, critical points, and analyzing the function's behavior to solve for extrema and inflection points.
Q & A
What is the primary focus of the video?
-The video focuses on curve analysis, discussing how to interpret function values and derivatives to determine the behavior of a function, such as whether it is increasing or decreasing, and identifying critical points, relative maxima, minima, and inflection points.
What is the significance of the reference chart provided in the video?
-The reference chart organizes information on how to interpret the values of a function and its derivatives. It serves as a guide for students to memorize the rules for curve analysis, which is essential for solving problems and expected to be known for an exam.
How do you determine if a point is a critical point?
-A point is considered a critical point if the first derivative of the function at that point is equal to zero.
What does it mean if the second derivative of a function is less than zero?
-If the second derivative of a function is less than zero, it indicates that the function is concave down at that point.
How can you identify an inflection point?
-An inflection point can be identified when the second derivative of a function is equal to zero, and the function changes its concavity from concave up to concave down or vice versa as you cross that point.
What is the process to find the absolute minimum value of a function on a closed interval?
-To find the absolute minimum value, one should first find the critical points by setting the first derivative equal to zero. Then evaluate the function at these critical points and at the endpoints of the interval. The smallest value among these evaluations is the absolute minimum.
Why is it necessary to check the endpoints of a closed interval when finding the absolute minimum or maximum of a function?
-It is necessary because the absolute minimum or maximum value might occur at one of the endpoints, not just at the critical points within the interval.
What is the relationship between velocity and acceleration?
-Acceleration is the derivative of velocity with respect to time, representing the rate of change of velocity.
How does the video determine the maximum acceleration for a given velocity function over a closed interval?
-The video finds the derivative of the velocity function to get the acceleration function, identifies critical points by setting the first derivative to zero, evaluates the acceleration function at the critical points and endpoints, and then selects the highest value as the maximum acceleration.
What is the quotient rule used for in the video?
-The quotient rule is used to find the derivative of a function that is the quotient of two other functions, such as the natural logarithm of x divided by x.
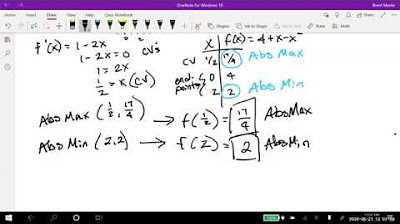
How does the video determine the value of k for the function y = x + k/x to have a relative maximum at x = -2?
-The video sets the first derivative equal to zero to find critical points, then uses the second derivative to check for concavity. By substituting x = -2 into the equation derived from the first derivative, it finds that k must be 1/4 for the function to have a relative maximum at that point.
Outlines
📊 Curve Analysis Overview
This paragraph introduces the topic of curve analysis, focusing on understanding a reference chart that organizes information about function values and their derivatives. The chart helps to identify when a function's values are negative, zero, or positive, and when the function is increasing, decreasing, or has a critical point based on the first derivative. It also covers concavity and inflection points determined by the second derivative. The importance of memorizing this information for exams is emphasized, and the concept of relative maxima and minima in relation to concavity is explained.
🔍 Finding Absolute Minimum Values
The second paragraph delves into finding the absolute minimum value of a function within a closed interval. It explains the process of identifying critical points by setting the first derivative to zero and solving for x. The paragraph also discusses evaluating these critical points and the endpoints of the interval to determine the absolute minimum. It highlights that the minimum value might not always occur at a critical point but could be at the interval's endpoints, as demonstrated through an example involving a cubic function.
📈 Maximum Acceleration Calculation
This section focuses on calculating the maximum acceleration of a particle whose velocity is given by a specific function. It outlines the relationship between velocity and acceleration, emphasizing that acceleration is the derivative of velocity. The process involves finding the first derivative of the velocity function, setting it to zero to find critical points, and evaluating these points to determine the maximum acceleration. The example concludes by identifying the time at which the maximum acceleration occurs and providing the corresponding coordinate pair.
🔑 Absolute Maximum Value of a Function
The fourth paragraph addresses finding the absolute maximum value of a function defined by a natural logarithm divided by x. It explains the use of the quotient rule to find the first derivative and setting it to zero to find critical points. The paragraph then discusses the importance of determining the concavity of the function to establish whether the critical point corresponds to a maximum or minimum. The use of a graphing calculator to visualize the function and confirm the maximum value is also mentioned.
🤔 Relative Maximum at a Specific Point
The final paragraph presents a problem involving a function that has a relative maximum at x equals negative two. It explores the process of finding the derivative of the function, setting it to zero to find critical points, and then solving for the variable k to ensure the relative maximum occurs at the specified x-value. The paragraph also covers calculating the second derivative to confirm the concavity of the function at the critical point, thereby verifying the presence of a relative maximum.
Mindmap
Keywords
💡Curve Analysis
💡First Derivative
💡Second Derivative
💡Critical Point
💡Relative Maximum/Minimum
💡Inflection Point
💡Closed Interval
💡Quotient Rule
💡Natural Logarithm
💡Power Rule
💡Concavity
Highlights
Curve analysis is introduced as a method to understand the behavior of functions, including their zeros, critical points, and concavity.
A reference chart is provided to help organize information on function values, derivatives, and concavity.
The concept of a zero of a function is explained, where the function value equals zero.
Critical points are identified as points where the first derivative is zero, indicating potential local maxima, minima, or inflection points.
The role of the second derivative in determining concavity (concave up or down) and potential inflection points is discussed.
Relative maxima and minima are shown to occur at critical points where the function's concavity changes.
The importance of checking endpoints in closed intervals for potential absolute maxima or minima is emphasized.
The process of finding absolute minimum values on a closed interval is demonstrated through an example problem.
The concept of acceleration as the derivative of velocity is used to find maximum acceleration on a given interval.
The quotient rule is applied to find the derivative of a function involving a natural logarithm.
Desmos is used to visualize and confirm the concavity of a function, aiding in determining the absolute maximum value.
An example problem is solved to find the value of k that results in a relative maximum at a specific point.
The second derivative test is used to confirm whether a critical point is a relative maximum or minimum by checking concavity.
The process of setting up and solving equations for critical points when the variable is not x, but another parameter like k, is demonstrated.
The video concludes with the solution that k must be one fourth for the function to have a relative maximum at x equals negative two.
The importance of understanding the relationship between the first and second derivatives and the function's behavior is highlighted throughout the video.
The video provides a comprehensive guide on how to analyze various aspects of a function's graph, including critical points and inflection points.
Practical examples are used to illustrate the process of finding absolute and relative extrema of functions on closed intervals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: