Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)
TLDRThis video script delves into the intricacies of trigonometric functions, focusing on reciprocal identities and their applications. It emphasizes the importance of understanding the unit circle's role in defining trig functions like sine and cosine, and how these can be extended to larger circles without altering the fundamental relationships. The script clarifies the concept that the radius size doesn't affect the angle's trig function value due to the consistent ratio between sides of similar triangles. It also stresses the necessity of knowing either two trig functions or a function with its respective quadrant to determine the signs of other trig functions. The video uses examples to illustrate how to find the remaining trig functions when given one or two, and how to apply this knowledge to non-unit circle scenarios. It aims to help viewers grasp the interplay between trigonometric functions and their reciprocals, simplifying the process of finding trig function values and preparing them for more advanced topics like calculus.
Takeaways
- 📐 The sine and cosine functions are defined in relation to the y and x coordinates of a point on a unit circle, respectively, with tangent being the ratio of sine to cosine.
- 🔄 Reciprocal trigonometric functions include cosecant (1/sine), secant (1/cosine), and cotangent (1/tan), which are the inverses of their respective functions.
- 🤔 Understanding the reciprocal identities is more important than memorizing formulas; taking the reciprocal of a fraction will yield the corresponding reciprocal trigonometric function.
- 🧭 Knowing two trigonometric functions allows determining the quadrant of the angle and the signs of the remaining trigonometric functions, which is crucial for functions like tangent.
- 🌀 The concept of a unit circle (radius = 1) is flexible and can be extended to larger circles without changing the fundamental relationships between trigonometric functions.
- 📉 The range of sine and cosine is from -1 to 1, and their values can represent points on a unit circle or be part of the sides of a right triangle inscribed in a larger circle.
- 🔺 The quadrant in which the angle resides is essential for determining the signs of the trigonometric functions, as the signs change across different quadrants.
- 🔽 When given a single trigonometric function and its quadrant, one can find other trig functions using the Pythagorean theorem or the equation of a circle to find missing sides of the triangle.
- 🤓 Recognizing the relationship between the trigonometric functions and their reciprocals allows for easier calculation of the functions without relying on formula sheets.
- 📌 The signs of the trigonometric functions are determined by the quadrant: sine and cosecant are positive where sine is positive, cosine and secant are positive where cosine is positive, and tangent and cotangent follow the signs of sine and cosine, respectively.
- 🔍 To find all trigonometric functions from one or two, understanding the relationships and reciprocal identities is key, as well as knowing the quadrant for the correct sign interpretation.
Q & A
What are reciprocal trigonometric functions?
-Reciprocal trigonometric functions are the inverses of the standard trigonometric functions. For example, the reciprocal of sine is cosecant (csc), the reciprocal of cosine is secant (sec), and the reciprocal of tangent is cotangent (cot).
How does knowing two trigonometric functions help in determining the angle's quadrant?
-Knowing two trigonometric functions allows you to determine the signs of the remaining trigonometric functions, which in turn helps you identify the quadrant in which the angle lies. This is important because the signs of the trigonometric functions vary depending on the quadrant.
Why does it not matter if the trigonometric function is on a unit circle or not when calculating the sine or cosine of an angle?
-It does not matter because the ratio of the sides of the triangle (y over the radius) remains constant regardless of the size of the circle. This is due to the concept of similar triangles, where the angles remain the same and the ratios of corresponding sides are equal.
What is the relationship between the sine and cosine of an angle and the coordinates of a point on the unit circle?
-The sine of an angle (sin θ) corresponds to the y-coordinate of a point on the unit circle, while the cosine of the angle (cos θ) corresponds to the x-coordinate of the point.
How can you find the other trigonometric functions if you know the sine and cosine of an angle?
-If you know the sine and cosine of an angle, you can use the reciprocal identities to find the cosecant and secant, and the quotient identities to find the tangent and cotangent. Knowing the angle's quadrant helps determine the signs of these functions.
What is the significance of the Pythagorean theorem in the context of trigonometric functions?
-The Pythagorean theorem is used to find the missing side of a right triangle when two sides are known. In the context of trigonometric functions, it helps find the third side (usually the adjacent or opposite side) when the hypotenuse and one other side (related to a trigonometric function) are known.
Why is it necessary to know the quadrant of an angle when only one trigonometric function is given?
-Knowing the quadrant is necessary to determine the signs of the other trigonometric functions because the signs vary depending on the quadrant. Without this information, you cannot determine the correct values for the other trigonometric functions.
How does the range of sine and cosine affect the consideration of a point being on a unit circle?
-The range of sine and cosine, which is between -1 and 1, allows for the consideration of a point being on a unit circle. If the value of sine or cosine is less than 1, it can be interpreted as a ratio of the y-coordinate to the radius (1 in the case of a unit circle) or as a fraction representing a y-value on the unit circle.
What is the relationship between tangent and cotangent in terms of reciprocals?
-Tangent (tan θ) is the ratio of sine to cosine (sin θ / cos θ), and cotangent (cot θ) is the reciprocal of tangent, which means cot θ = cos θ / sin θ or the reciprocal of tan θ.
Why is it important to understand the relationship between the trigonometric functions rather than just memorizing their formulas?
-Understanding the relationships between the trigonometric functions allows for a deeper comprehension of how they interact and depend on each other. This understanding is crucial for solving more complex problems and for visualizing the functions geometrically, which can be particularly helpful in higher mathematics.
How can you determine the signs of the trigonometric functions without knowing the exact angle?
-By knowing the values of two trigonometric functions and the quadrant in which the angle lies, you can determine the signs of the other trigonometric functions. This is because the signs of the functions are dependent on the quadrant, which can be inferred from the given function values.
Outlines
📚 Introduction to Trig Functions and Reciprocal Identities
The video begins with an introduction to trigonometric functions, focusing on the sine and cosine of theta, which are related to the coordinates (x, y) on a unit circle. The presenter emphasizes understanding the relationship between sine, cosine, tangent, and their reciprocal functions—cosecant, secant, and cotangent—rather than memorizing formulas. The video also discusses the importance of knowing whether a function is on a unit circle or not, and how to deal with trig functions given one or two of them along with the quadrant information.
🔍 Understanding Trig Functions with Quadrant Information
The paragraph explains why two trig functions are often given—to determine the angle's location in a specific quadrant, which is crucial for finding the signs of other trig functions. It also explores the concept of similar triangles and how the size of the triangle (or radius) does not affect the relationship between the trig function's values. The presenter clarifies that knowing the quadrant is essential for determining the signs of the trig functions, especially for tangent and cotangent.
🧮 Applying Reciprocal Identities to Find Trig Functions
This section demonstrates how to use reciprocal identities to find the values of trig functions when given the values of sine and cosine. It shows that understanding the reciprocal relationship between sine and cosecant, cosine and secant, and tangent and cotangent allows for easy calculation of the remaining trig functions. The importance of knowing the angle's quadrant is also highlighted to determine the correct signs for the functions.
🔢 Using Pythagorean Theorem to Find Missing Trig Function Values
The video script explains how to use the Pythagorean theorem to find missing trig function values when you have a y value and an r value. It emphasizes that the angle's sine value remains consistent regardless of the triangle's size, which is why similar triangles maintain the same trig function ratios. The presenter also discusses the importance of considering the correct quadrant to determine the signs of the trig function values accurately.
🤔 Determining the Sign of Trig Functions with a Single Given Function
The paragraph discusses the challenge of determining the angle's quadrant with only one trig function given. It explains that without knowing the y value's sign, it's impossible to determine the sine, cosecant, tangent, or cotangent values. The video stresses the need to know a second trig function or the angle's quadrant to find the correct signs for all trig functions.
📐 Exploring the Relationship Between Trig Functions and the Unit Circle
This section delves into the relationship between trig functions and the unit circle, explaining that the angle's sine value can be considered as a y value on a unit circle or as part of a right triangle inscribed in a circle with any radius. The presenter uses the Pythagorean theorem to find the missing side of the triangle, which helps in determining the remaining trig function values. The importance of considering the correct orientation of the triangle and the implications of square roots when solving for x are also discussed.
📉 Determining Quadrants and Trig Function Signs
The paragraph explains the necessity of knowing the angle's quadrant to determine the signs of the trig functions. It details how the signs of sine, cosine, and their reciprocals can be used to identify the correct quadrant, which is essential for finding the correct x and y values. The video also shows how to calculate the remaining trig functions once the quadrant is known.
🔁 Reciprocal Trig Functions and Their Significance
The video concludes with a recap of the reciprocal relationships between trig functions—cosecant with sine, secant with cosine, and cotangent with tangent. It emphasizes the importance of understanding these relationships rather than memorizing formulas. The presenter also hints at future discussions on the even or odd nature of sine and cosine and the Pythagorean identities, encouraging viewers to join for the next video.
Mindmap
Keywords
💡Reciprocal Trigonometric Functions
💡Unit Circle
💡Trigonometric Identities
💡Quadrants
💡Pythagorean Theorem
💡Sine and Cosine
💡Tangent and Cotangent
💡Cosecant and Secant
💡Similar Triangles
💡Trigonometric Functions and Angles
💡Positive and Negative Signs
Highlights
The video discusses the concept of reciprocal trigonometric functions and their applications.
Explains how to use reciprocal identities to find other trigonometric functions given one or two known functions.
Clarifies the relationship between sine and cosine with their respective reciprocals, cosecant and secant.
Demonstrates how to determine the quadrant of an angle using two given trigonometric functions.
Introduces the idea that the value of trigonometric functions remains consistent across different sized circles due to similar triangles.
Provides a method to find the remaining trigonometric functions if two functions and the quadrant are known.
Explains the importance of understanding the reciprocal relationship between tangent and cotangent.
Shows how to use the Pythagorean theorem to find a missing side of a triangle when two trigonometric functions are known.
Discusses the necessity of knowing the angle's quadrant to determine the signs of the trigonometric functions.
Illustrates the process of finding all trigonometric functions from a given angle using reciprocal identities and the unit circle concept.
Details the significance of the signs of trigonometric functions in determining the correct values in different quadrants.
Provides an example of calculating all trigonometric functions given the value of secant and the angle's quadrant.
Explains the concept of similar triangles and how they relate to the unit circle and trigonometric functions.
Demonstrates the process of rationalizing denominators when dealing with trigonometric function values.
Stresses the importance of understanding the underlying concepts rather than just memorizing formulas.
Summarizes the video by emphasizing the interplay between trigonometric functions and their reciprocals, regardless of the circle's size.
The video concludes with a preview of upcoming topics, including even and odd properties of sine and cosine, and Pythagorean identities.
Transcripts
Browse More Related Video

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles
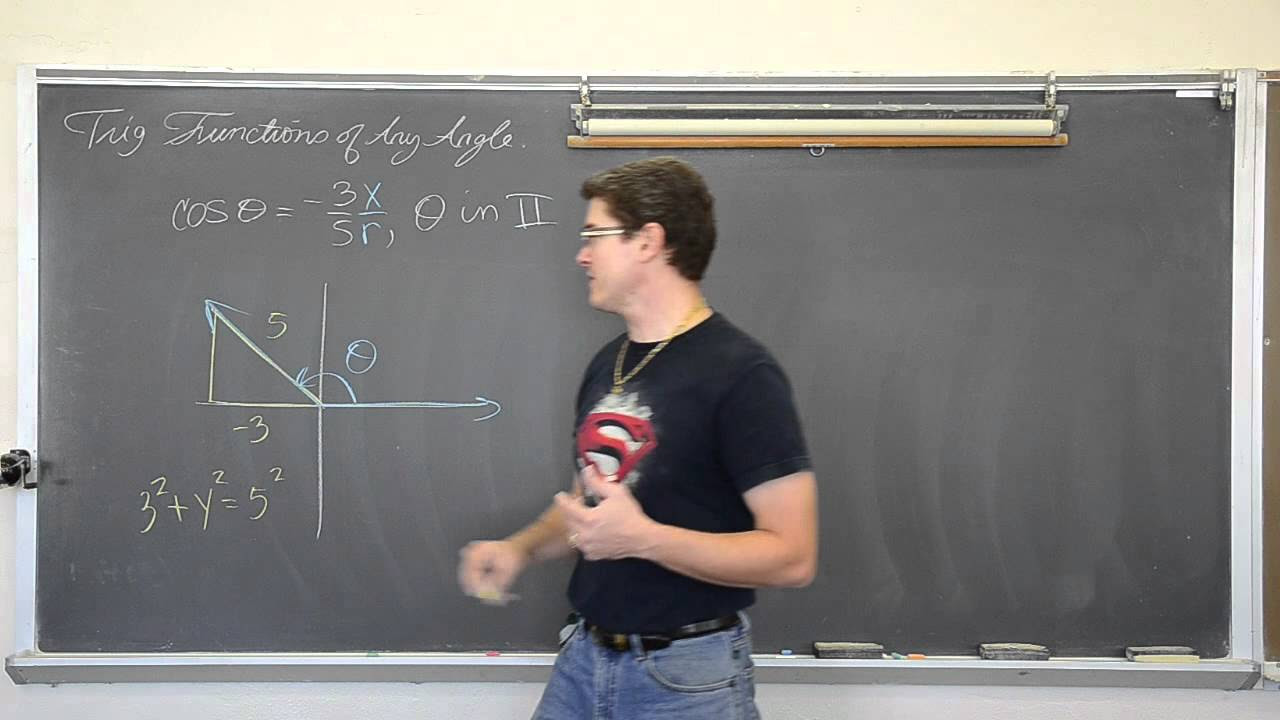
Trigonometric Functions of Any Angle

The Easiest Way to Memorize the Trigonometric Unit Circle

Solving Trigonometric Equations

Formulas for Trigonometric Functions: Sum/Difference, Double/Half-Angle, Prod-to-Sum/Sum-to-Prod
5.0 / 5 (0 votes)
Thanks for rating: