How Much Energy is Required to Change the Orbit of a Satellite?
TLDRThe video script explores the energy required to change a satellite's orbit from an initial radius to a final radius around a central object, using the work-energy theorem. It explains that the satellite's mechanical energy is the sum of its kinetic and potential energies, both of which are functions of the orbital radius. The script highlights that the mechanical energy of an object in orbit is negative, indicating it is trapped in the gravitational well. Finally, it outlines the calculation for the work needed to perform such an orbital maneuver, providing foundational knowledge for understanding satellite motion and energy transfer.
Takeaways
- 🚀 The problem examines the energy required to change a satellite's orbit from an initial radius to a final radius in a circular path around the Earth or any central object.
- 🌐 The work-energy theorem is applied to understand the change in mechanical energy of the satellite when transitioning between orbits.
- 🔄 Both initial and final mechanical energies are considered, along with the non-conservative work done, primarily by a rocket, to solve for the energy required for the orbit change.
- ⚙️ The mechanical energy of an object in orbit is a combination of its kinetic and potential energies, which can be expressed as a function of the orbit's radius.
- 🌍 The velocity of a satellite in orbit is a function of the radius due to the gravitational force acting as the centripetal force, as derived from Kepler's laws and Newton's evaluation.
- 📉 The mechanical energy of a satellite in a stable orbit is negative, indicating that it is trapped in the gravitational well and cannot escape without additional energy.
- 🔄 The concept of a gravity well is likened to a physical analogy of a coin trapped in a bowl at a mall, requiring more energy to escape than it has to continue orbiting.
- 🚀 The actual work required to change a satellite's orbit is found by calculating the difference in mechanical energy between the final and initial orbits.
- 🌑 Gravitational potential energy is calculated using a refined version of the formula, which is negative and inversely proportional to the radius.
- 🚀 The kinetic energy of an object in orbit is given by a formula that does not depend on the velocity directly but on the gravitational constant, mass of the central object, and the radius of the orbit.
- 🛰️ The process of moving a satellite from one orbit to another is more complex in practice and involves maneuvers known as Hohmann transfers, which will be discussed in later topics related to momentum and angular momentum.
Q & A
What is the main focus of the problem discussed in the transcript?
-The main focus of the problem is to determine the energy required to change the orbit of a satellite from an initial circular orbit to a final circular orbit.
What is the role of the work-energy theorem in this problem?
-The work-energy theorem is used to relate the initial and final mechanical energies of the satellite, plus the work done by a non-conservative force (like a rocket), to the energy required to change the satellite's orbit.
How does the satellite's kinetic energy in orbit relate to its radius?
-The kinetic energy of a satellite in orbit at a radius 'r' can be expressed as (1/2)mv^2, where 'v' is the velocity of the satellite, which is a function of 'r' and is determined by setting the centripetal force equal to the gravitational force.
What is the formula for the gravitational potential energy of an object in orbit?
-The gravitational potential energy of an object in orbit is given by the formula -(GMm)/R, where 'G' is the gravitational constant, 'M' is the mass of the central object (like Earth), 'm' is the mass of the satellite, and 'R' is the distance from the center of the central object to the satellite.
Why is the mechanical energy of a satellite in orbit negative?
-The mechanical energy of a satellite in orbit is negative because the gravitational potential energy is negative and the kinetic energy is positive; the potential energy is always greater in magnitude, indicating that the satellite is trapped in the gravitational well and cannot escape without adding energy.
How does the concept of a gravity well relate to a satellite in orbit?
-A gravity well is a metaphorical concept that describes the potential energy environment around a massive object like a planet or a star. A satellite in orbit has negative mechanical energy, meaning it is trapped in this gravity well and lacks the energy to escape.
What is the significance of Kepler's laws and Newton's evaluation of them in this problem?
-Kepler's laws and Newton's evaluation of them are significant because they provide the relationship between the satellite's orbital radius and its velocity, which is essential for calculating the kinetic energy and, ultimately, the energy required to change orbits.
How does the work done by a rocket during an orbit change relate to the change in mechanical energy?
-The work done by a rocket during an orbit change is the non-conservative work term in the work-energy theorem. This work is what provides the satellite with the additional energy needed to move from one orbit to another.
What is the final expression derived for the work required to change a satellite's orbit?
-The final expression derived for the work required to change a satellite's orbit is the difference between the final mechanical energy (at the final radius) and the initial mechanical energy (at the initial radius).
What additional concepts will be important for understanding more about changing satellite orbits?
-Additional concepts that will be important for understanding more about changing satellite orbits include momentum and angular momentum, which will be discussed in later sections.
What is the practical implication of the energy calculation for satellites?
-The practical implication of the energy calculation is that it provides the amount of energy required to change a satellite's orbit, which is crucial for designing and executing space missions that involve maneuvers such as moving from one orbit to another.
Outlines
🚀 Energy Required to Change Satellite Orbits
This paragraph discusses the problem of calculating the energy needed to move a satellite from an initial circular orbit to a final circular orbit of different radius. It introduces the concept by referencing the work-energy theorem and the mechanical energy of the satellite, which consists of its initial kinetic and potential energy. The paragraph explains that the satellite's kinetic energy is a function of the radius due to its orbital velocity, which is derived from the gravitational force acting as the centripetal force. The potential energy is identified as gravitational potential energy, and the relationship between the radius and the velocity is established using Newton's law of universal gravitation. The paragraph concludes by mentioning that the goal is to find the non-conservative work term, which is the work done by a rocket to change the satellite's orbit.
🌌 Understanding Orbital Mechanical Energy and Orbit Change
This paragraph delves into the implications of the mechanical energy derived in the previous section, highlighting that the mechanical energy of a satellite in orbit is negative, indicating that it is trapped in the gravitational well and cannot escape. The kinetic energy is always positive, while the gravitational potential energy is always negative, and their sum results in a negative total mechanical energy. The analogy of a coin in a bowl at a mall is used to explain the concept of being trapped in a potential well. The paragraph then transitions to discussing the work required to change orbits, which involves evaluating the derived mechanical energy function for different masses and radii. It notes that in practice, changing a satellite's orbit involves additional considerations, such as the Hohmann transfer orbit, which will be discussed in future lessons related to momentum and angular momentum. The paragraph concludes by summarizing that the problem has solved for the mechanical energy of an object in orbit and the work needed to change its orbit.
Mindmap
Keywords
💡energy required
💡satellite
💡work-energy theorem
💡gravitational potential energy
💡kinetic energy
💡mechanical energy
💡non-conservative work
💡Kepler's laws
💡centripetal force
💡gravity well
💡Hohmann transfer orbit
Highlights
The problem examines the energy required to move a satellite from an initial circular orbit to a final circular orbit.
The energy required is calculated based on the work-energy theorem, involving the initial and final mechanical energy and the work done by a non-conservative force, such as a rocket.
Mechanical energy is composed of kinetic and potential energies, which can be formulated into a function for an object in orbit around a central object like Earth.
The velocity of a satellite in orbit is a function of the orbit's radius, which can be derived from Kepler's laws and Newton's evaluation of these laws.
The relationship between the radius and the velocity of a satellite in orbit is given by v^2 = GM/r, where M is the mass of the central object (e.g., Earth).
The kinetic energy of an object in orbit can be expressed as (GMm)/2r, with the mass of the central object canceling out.
Gravitational potential energy is calculated using the formula -GMm/r, where the central object's mass is included in the equation.
The mechanical energy of a satellite in a circular orbit is the sum of its kinetic and potential energies, resulting in a negative value indicating the satellite is trapped in the gravity well.
The negative mechanical energy signifies that the satellite does not have enough energy to escape the gravitational pull of the central object.
The analogy of a coin in a bowl at a mall illustrates the concept of an object being trapped in a potential well, similar to a satellite in orbit.
The work required to change the orbit of a satellite is found by calculating the difference in mechanical energy between the final and initial orbits.
The practical process of changing a satellite's orbit involves more factors, such as the Hohmann transfer orbit, which will be discussed in later topics related to momentum and angular momentum.
The problem provides a foundational understanding of the energy dynamics involved in satellite orbit changes, which is crucial for space mission planning and satellite maneuvering.
The derivation of the mechanical energy function for a satellite in orbit is essential for further studies in orbital mechanics and space dynamics.
The work done to change orbits can be seen as the energy input needed to move from one gravitational potential well to another.
Understanding the relationship between the radius and velocity of a satellite in orbit is fundamental to the application of orbital mechanics in space travel and satellite technology.
The concept of mechanical energy being negative for objects in orbit is a key takeaway from the discussion, highlighting the importance of energy conservation in orbital dynamics.
Transcripts
Browse More Related Video

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs
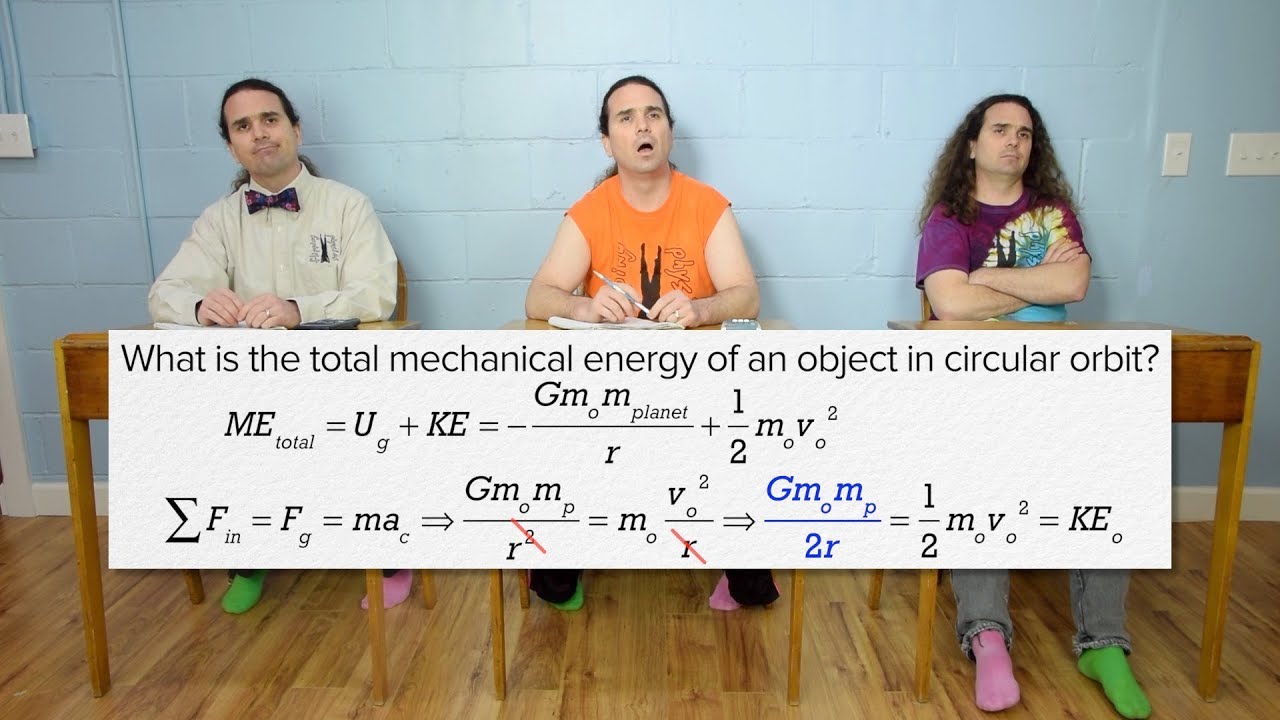
AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

Kinetic Energy and Potential Energy
Rotational Power, Work, Energy, Torque & Moment of Inertia - Physics Problems
Work-energy theorem | Work & Energy | Physics | Khan Academy

Lecture 9 - Some relations from the Bohr's theory
5.0 / 5 (0 votes)
Thanks for rating: