Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs
TLDRThis video delves into the concept of gravitational potential in the context of A-Level Physics, distinguishing it from gravitational field strength and force. It begins with defining gravitational potential as the work done to bring unit mass from infinity to a point, highlighting its relationship with gravitational energy. The video then tackles a problem involving a satellite orbiting Earth, using both gravitational force and potential to calculate the satellite's orbital radius. It proceeds to explain the difference in gravitational potential energy between the satellite's orbit and its position on a launch pad on Earth's surface. The video also explores the relationship between gravitational potential and field strength, using theoretical examples and graphical analysis to illustrate these concepts. Finally, it addresses a scenario with a moon orbiting a planet, discussing the gravitational potential gradient and field strength at various points. The video is a comprehensive guide to understanding and solving problems related to gravitational potential.
Takeaways
- 🌌 Gravitational potential is the energy per unit mass, defined as the work done to bring a unit mass from infinity to a specific point in a gravitational field.
- 📈 Gravitational potential is distinct from gravitational field strength and the force exerted on an object, focusing on energy rather than force.
- 🪐 At infinite distance from any mass, the gravitational potential is considered zero, as there is no force acting on the object.
- 🚀 To move an object from within a gravitational field to infinity, work must be done against the gravitational force, resulting in a negative value for gravitational potential within the field.
- 📊 The satellite's orbital radius can be calculated using the gravitational force as the centripetal force, with the formula rearranged to solve for radius.
- 🌍 The change in gravitational potential energy is found by multiplying the mass of the object by the gravitational potential at the respective points.
- 📉 Gravitational potential energy (GPE) decreases as an object gets closer to a massive body due to the attractive nature of gravity.
- 📈 The gravitational field strength is related to the gravitational potential by taking the negative gradient of the potential, represented by the formula GM/r^2.
- 🌕 The maximum gravitational potential in a two-body system (e.g., planet-moon) is closer to the body with lesser mass (moon) due to the steeper potential gradient.
- 🔄 The gravitational field strength at a point between two masses can be sketched by considering the inverse relationship between potential and distance, and the balance of forces between the two masses.
- 🎥 Visualizing gravitational potential as a trampoline surface helps in understanding the potential wells and gradients created by different masses pressing down on it.
Q & A
What is the definition of gravitational potential?
-Gravitational potential is defined as the work done in bringing a unit mass from infinity to a specific point. It represents the gravitational energy an object possesses at that point.
How does gravitational potential differ from gravitational field strength and force exerted on an object?
-Gravitational potential pertains to the energy aspect of an object's position in a gravitational field, while gravitational field strength and force are related to the actual physical force exerted on an object due to gravity.
Why is the gravitational potential at a point where an object is not at infinity negative?
-The gravitational potential is negative at any point where the object is not at infinity because energy is required to move the object away from the influence of other masses back to infinity, where the potential is considered zero.
How does the mass of a satellite and the time it takes to orbit the Earth help determine its orbital radius?
-By using the formulas for gravitational force and centripetal force, and knowing the satellite's mass, orbital period, and the mass of the Earth, one can calculate the radius of the satellite's orbit through algebraic manipulation and substitution of the given values.
What is the formula for gravitational potential energy, and how is it related to the potential at a point?
-The formula for gravitational potential energy is given by U = m*Phi, where m is the mass of the object and Phi is the gravitational potential at that point. The potential energy is the product of the potential at a point and the mass of the object present at that point.
How does the change in gravitational potential energy between a satellite in orbit and on the Earth's surface get calculated?
-The change in gravitational potential energy (Delta E) is calculated by taking the difference between the potential at the satellite's orbit (negative GM/orbital radius) and the potential at the Earth's surface (negative GM/Earth's radius), resulting in a positive value representing the energy required to move the satellite from the surface to orbit.
What is the relationship between gravitational potential and gravitational field strength?
-Gravitational field strength is the gradient of the gravitational potential, which means that the field strength at any point is equal to the negative of the derivative of the potential with respect to distance. Essentially, the field strength is the rate of change of potential.
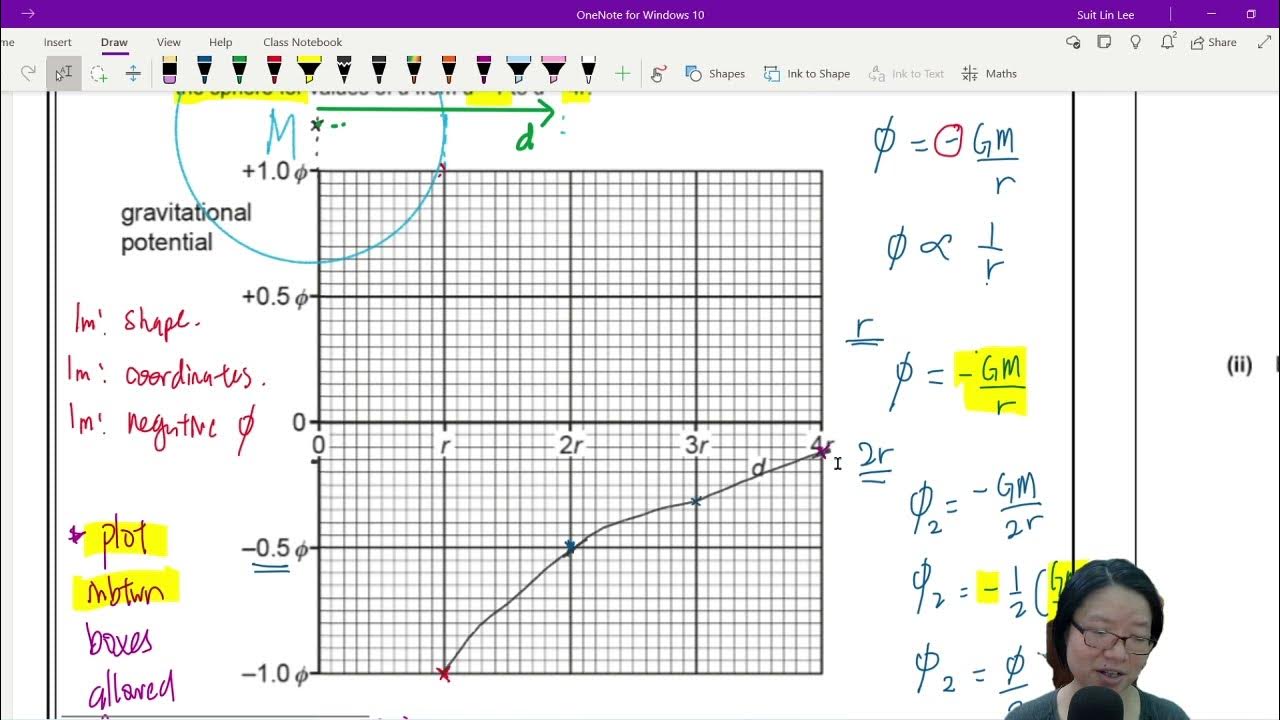
Why does the gravitational potential graph for a point between two masses (like a planet and a moon) not hit zero?
-The gravitational potential graph does not hit zero because it represents the energy of an object at a point, which is always negative within the influence of masses (potential wells), as opposed to gravitational field strength, which can balance out and become zero at certain points due to opposing forces.
What can the maximum gravitational potential value on the graph between two masses tell us?
-The maximum gravitational potential value on the graph indicates the relative influence of the two masses. It is closer to the mass with lesser influence (in this case, the moon) because the potential gradient of the more massive body (the planet) is steeper, representing a stronger gravitational pull.
How can the gravitational field strength at a point between two masses be sketched?
-The gravitational field strength at a point between two masses can be sketched by considering the direction and magnitude of the forces exerted by each mass. The field strength will vary, reaching zero at a point where the forces balance out, and the direction will be towards the more massive body due to its stronger gravitational pull.
What is the significance of understanding the relationship between gravitational potential and gravitational field strength?
-Understanding the relationship between gravitational potential and gravitational field strength is crucial for analyzing the energy dynamics and forces at play in celestial mechanics. It helps in predicting the behavior of objects in gravitational fields and calculating the energy changes associated with their motion.
Outlines
📚 Introduction to Gravitational Potential
This paragraph introduces the concept of gravitational potential, distinguishing it from gravitational field strength and force. Gravitational potential is related to the energy an object has due to gravity. The definition provided is the work done to bring a unit mass from infinity to a specific point. The script also explains that at an infinite distance from any mass, the force is zero, and thus the potential is considered zero. The video aims to clarify this concept and its relation to energy.
🛰️ Satellite Orbit Calculation
The second paragraph deals with a physics problem involving a satellite of mass 360 kg orbiting the Earth. The problem requires calculating the radius of the satellite's orbit using the given period of orbit and the mass of the Earth. The solution involves converting the period into seconds and equating the centripetal force (required for circular motion) to the gravitational force. After rearranging the formula and substituting the given values, the radius of the orbit is found to be 2.4 x 10^8 meters.
⚡️ Gravitational Potential Energy Calculation
This part of the script focuses on calculating the change in gravitational potential energy as a satellite moves from its orbit to a position on the Earth's surface. The formula for gravitational potential, Phi = -GM/r, is introduced, where G is the gravitational constant, M is the mass of the Earth, and r is the distance from the center of the Earth. The change in potential energy (Delta E) is calculated by finding the difference in potential at the satellite's orbit and on the Earth's surface, resulting in 2.2 x 10^10 joules.
🌌 Gravitational Field Strength and Potential Gradient
The fourth paragraph explains the relationship between gravitational potential and gravitational field strength. It states that the field strength is the gradient of the potential, which can be found by dividing the potential by the distance (R). The script also discusses a scenario involving a moon and a planet, using a graph to illustrate the gravitational potential at various points between them. It is explained that the potential is negative throughout the range because gravitational force is attractive, causing potential energy to decrease as mass approaches from infinity.
📈 Analyzing Gravitational Potential Graphs
The final paragraph delves into analyzing gravitational potential graphs, particularly focusing on the characteristics of the graph provided. It describes features such as the negative potential throughout the graph, the maximum potential being closer to the moon than the planet due to the steeper potential gradient of the more massive Earth, and the inverse proportionality of potential to distance from the planet or moon. The paragraph concludes with an exercise to sketch the variation of gravitational field strength at a point between the planet and the moon, noting that the field strength will hit zero at a certain point as the opposing forces balance each other out.
Mindmap
Keywords
💡Gravitational Potential
💡Work Done
💡Satellite
💡Orbit
💡Centripetal Force
💡Gravitational Field Strength
💡Gravitational Potential Energy
💡Gravitational Force
💡Energy
💡Infinite Distance
💡Potential Well
💡Trampoline Analogy
Highlights
Gravitational potential is fundamentally different from gravitational field strength and force.
Gravitational potential is about the gravitational energy an object has.
The definition of gravitational potential is the work done in bringing unit mass from infinity to a point.
At infinite distance from any mass, the force and hence the gravitational potential is zero.
The potential at a point where an object is not at infinity will have a negative value.
The question involves a satellite named 'tess' with a mass of 360 kg orbiting the Earth.
The period of 'tess' orbiting the Earth is given as 13.7 days.
Centripetal force is provided by gravitational force in the orbit of 'tess'.
The radius of 'tess' orbit is calculated to be 2.4 x 10^8 meters.
Gravitational potential energy change is calculated between 'tess' in orbit and on the Earth's surface.
The formula for gravitational potential energy is the product of mass and the potential.
The change in gravitational potential energy is found to be 2.2 x 10^10 joules.
The ratio of gravitational field strength on Earth's surface and at 'tess' orbit is calculated.
Gravitational field strength is inversely proportional to the square of the distance from the mass.
The relationship between gravitational potential and gravitational field strength is explained.
The gravitational potential graph for a moon orbiting a planet is analyzed.
The potential is negative throughout the entire range because it's in a potential well.
The maximum potential is closer to the Moon than the planet due to the Earth's steeper potential gradient.
The gravitational field strength variation at a point between the Earth and the Moon is sketched.
Gravitational potential questions often involve potential wells and analyzing graphs.
Transcripts
Browse More Related Video

Gravitational Potential and Gravitational Potential Energy

What is Gravitational Potential Energy - a deeper understanding

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics
13.3b Ex1 MJ20 P42 Q1 Rock Potential Energy | A2 Gravitational Fields | Cambridge A Level Physics

Mr Chua, can you explain the F=-dU/dx formula?

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: