Work-energy theorem | Work & Energy | Physics | Khan Academy
TLDRThe video script introduces the work-energy theorem, a fundamental concept in physics that links the work done on an object to its change in kinetic energy. It explains how positive work increases an object's kinetic energy, while negative work decreases it. The theorem is mathematically derived, showing that the total work done (net work) on an object is equal to the change in its kinetic energy. This principle is illustrated with examples such as throwing and catching a ball, dropping a bowling ball, and moving a cupboard on a rough floor. The concept is crucial for solving problems in mechanics and provides a new perspective on force and motion.
Takeaways
- 🏌️ Work and energy concepts help us view the world differently, particularly in understanding how objects accelerate and decelerate.
- 🔢 Newton's second law (F=ma) is fundamental in explaining how force leads to acceleration and thus changes in speed and kinetic energy.
- 🏐 When throwing a bowling ball, the force exerted by the hand does work on the ball, increasing its kinetic energy.
- 🔄 Negative work, such as when catching a ball or friction acting against motion, results in the removal of kinetic energy from an object.
- 📈 The work-energy theorem states that the work done on an object either adds to or removes kinetic energy, depending on whether the work is positive or negative.
- 🚀 The mathematical representation of the work-energy theorem is given by the equation: Work = Change in Kinetic Energy (Final KE - Initial KE).
- 🔄 When multiple forces act on an object, the net work (total work done by all forces) determines the change in kinetic energy.
- 🛠️ Problem-solving in physics can be expedited by using the work-energy theorem instead of solely relying on F=ma for certain types of problems.
- 🔧 The work done by all forces on an object can be calculated by summing the individual works, taking into account their directions and magnitudes.
- 📊 The work-energy theorem is a powerful tool for analyzing situations where forces do positive or negative work, and how these affect an object's kinetic energy state.
Q & A
What is the primary purpose of introducing work and energy concepts in physics?
-The primary purpose of introducing work and energy concepts is to provide a different perspective for understanding and analyzing physical phenomena, particularly how forces can change an object's motion and kinetic energy.
According to Newton's second law, what happens when you apply a force on an object?
-According to Newton's second law, when you apply a force on an object, it causes the object to accelerate. This is expressed by the formula F=ma, where F is the force, m is the mass of the object, and a is the acceleration it experiences.
What is the relationship between work done and an object's kinetic energy?
-When work is done on an object, it results in a change in the object's kinetic energy. Positive work adds kinetic energy to the object, while negative work removes it. The amount of work done corresponds to the amount of kinetic energy added or removed.
How does the work-energy theorem describe the effect of work on an object's kinetic energy?
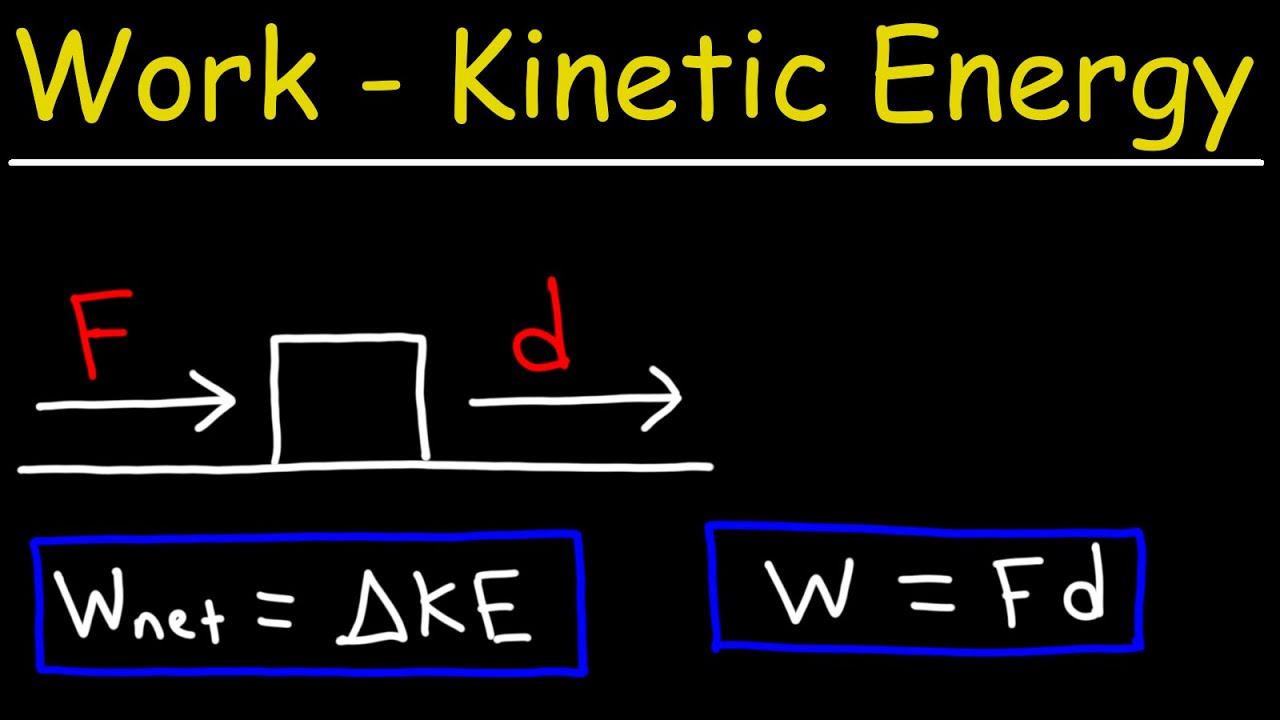
-The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. Mathematically, it is represented as W = ΔKE = K_f - K_i, where W is the work done, K_f is the final kinetic energy, and K_i is the initial kinetic energy.
What happens when multiple forces act on an object?
-When multiple forces act on an object, you must calculate the net force by summing up all the forces (considering their directions). Similarly, the total work done on the object is the sum of the work done by each force, which determines the change in the object's kinetic energy.
How does friction affect the work done on an object?
-Friction acts in the opposite direction to the displacement and thus can do negative work on an object. If the work done by pushing an object is equal and opposite to the work done by friction, the total work done on the object can be zero, resulting in no change in kinetic energy.
What is the significance of the work-energy theorem in problem-solving?
-The work-energy theorem is significant in problem-solving as it provides a convenient way to analyze the change in an object's kinetic energy due to various forces. It can simplify the process by directly relating the work done to the change in kinetic energy, without the need to calculate acceleration and displacement for each force separately.
How can the work done by gravity be described in terms of kinetic energy?
-When gravity does positive work (e.g., when an object falls), it adds kinetic energy to the object because gravity and displacement are in the same direction. Conversely, when gravity does negative work (e.g., when an object is moved upward against gravity), it removes kinetic energy because gravity and displacement are in opposite directions.
What is the mathematical derivation of the work-energy theorem?
-The work-energy theorem can be derived by starting with the work done by a force (F*s), substituting F with ma, and then using the equation of motion (v^2 = u^2 + 2as) to relate acceleration (a), displacement (s), and velocities (v and u). This leads to the theorem's equation: W = ΔKE = (m(v^2 - u^2)) / 2.
In the example with the puppy, why does the total work done end up being zero even though there is a displacement?
-The total work done on the puppy is zero because the positive work done by pushing upwards is exactly canceled out by the negative work done by gravity pulling downwards. This results in no net change in the puppy's kinetic energy.
What happens to the kinetic energy of an object when the total work done on it is positive?
-When the total work done on an object is positive, the object's kinetic energy increases by the amount of work done. This is because positive work adds energy to the object, resulting in a higher final kinetic energy compared to the initial kinetic energy.
Outlines
🏌️ Introduction to Work and Energy Concepts
The instructor begins by emphasizing the importance of understanding work and energy, and how these concepts can change our perspective on the world. Using the example of a bowling ball being thrown, the instructor explains how force leads to acceleration according to Newton's second law (F=ma). The concept of work is introduced by describing how the force applied to the ball results in displacement and an increase in the ball's kinetic energy. The work-energy theorem is informally introduced, stating that work done on an object either adds or removes kinetic energy. The instructor also discusses the scenario of negative work, such as catching a ball, where the work done results in a decrease in kinetic energy. Examples of objects under the influence of gravity are used to further illustrate the theorem, showing how positive work by gravity increases kinetic energy during free fall, while negative work slows down a ball thrown upwards. The concept of net force and net work is introduced, explaining how multiple forces can result in no change in kinetic energy if the work done by each force cancels out.
🔄 Work and Kinetic Energy: The Work-Energy Theorem
The paragraph delves deeper into the work-energy theorem by discussing how work done can be positive or negative, depending on the direction of the force relative to displacement. The total work done can be zero if positive and negative work cancel each other out, resulting in no change in kinetic energy. The instructor uses the examples of a heavy cupboard on a rough floor and a puppy being pushed upwards to illustrate this concept. The role of friction and gravity in these scenarios is explained, showing how they counteract the work done by the person, leading to no net change in kinetic energy. The paragraph concludes with the instructor prompting the viewer to consider the mathematical derivation of the work-energy theorem, setting the stage for the next part of the discussion.
📜 Mathematical Derivation of the Work-Energy Theorem
In this paragraph, the instructor provides a mathematical derivation of the work-energy theorem. Starting with the basic equation for work done by a force (force times displacement), the instructor uses Newton's second law (F=ma) to relate force to mass and acceleration. By incorporating the equations of motion, the instructor derives the relationship between initial and final velocities, displacement, and acceleration. The final step is to express the work done in terms of the change in kinetic energy, leading to the mathematical expression of the work-energy theorem. The theorem is then explained in terms of its implications for the kinetic energy of an object when work is done on it. The summary highlights the direct relationship between the amount of work done and the change in kinetic energy, and how this principle can be applied to problem-solving in physics.
Mindmap
Keywords
💡Work
💡Energy
💡Kinetic Energy
💡Force
💡Acceleration
💡Newton's Second Law
💡Displacement
💡Friction
💡Work-Energy Theorem
💡Net Force
💡Negative Work
Highlights
Introduction of work and energy concepts to see the world in a different way.
Explanation of acceleration and speed increase using Newton's second law when a force is applied.
Relation of force application and acceleration to the concept of doing work on an object.
Conversion of work into kinetic energy, exemplified by a thrown bowling ball gaining speed.
Demonstration of negative work through catching a ball, which reduces the ball's kinetic energy.
Discussion of the work-energy theorem, which states that work done changes an object's kinetic energy.
Exploration of gravity doing positive work on a falling object, increasing its kinetic energy.
Analysis of gravity doing negative work when an object is thrown upward, which slows it down.
Clarification of the net force and total work when multiple forces are acting on an object.
Example of a cupboard on a rough floor, where total work done is zero due to balanced forces.
Discussion of situations where the kinetic energy remains unchanged despite the application of force.
Introduction to the mathematical derivation of the work-energy theorem using force, displacement, and velocity.
Equation connecting work done to changes in kinetic energy, highlighting conservation and transformation.
Emphasis on how practical problem solving in physics can be more efficient using the work-energy theorem than Newton's second law alone.
Summary of the work-energy theorem's impact on understanding and predicting the effects of forces on objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: