How to find the radius when the area and circumference are changing at the same rate

Brian McLogan
7 Dec 201703:39
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a mathematical problem involving the rate of change of a circle's radius. It begins by establishing that the radius is increasing and introduces the concept of dr/dt. The script then transitions into calculating the area (A) of the circle using the formula A = Ο€r^2 and relates it to the circumference (C) with the formula C = 2Ο€r. The key point is that the rate of increase of the area is equal to the rate of increase of the circumference, which is expressed as dA/dt = dC/dt. The problem is solved by setting up an equation involving derivatives and simplifying it to find the radius (r) at a particular instant, concluding that r equals one.

Takeaways
  • πŸ“ The problem involves a circle whose radius is increasing at a non-zero rate.
  • πŸ”„ The initial step is to represent the radius and acknowledge the expanding nature of the circle, introducing the concept of 'dr/dt'.
  • πŸ”’ The area of the circle is given by the formula A = Ο€r^2, which is a fundamental relationship used in the problem.
  • πŸŒ€ The rate of increase in the area of the circle is numerically equal to the increase in the circumference.
  • πŸ“ The circumference of the circle is expressed as C = 2Ο€r, which is another basic formula relevant to the problem.
  • πŸ’‘ The equality of the rate of change in area and circumference is emphasized, leading to the derivatives dA/dt = dC/dt.
  • 🧠 The calculation of derivatives involves differentiating the area and circumference with respect to time 't', resulting in expressions involving 'dr/dt'.
  • πŸ“ˆ By setting the expressions for the derivatives of area and circumference equal to each other, a relationship between 'r' and 't' is sought.
  • πŸ” The problem simplifies the equation by dividing both sides by 'dr/dt' and other common factors to isolate 'r'.
  • 🎯 The conclusion drawn from the simplified equation is that 'r' equals one, marking the solution to the problem.
Q & A

  • What is the main concept discussed in the video script?

    -The main concept discussed in the video script is the relationship between the rate of increase of a circle's radius and the rate of increase of its area and circumference.

  • How does the script introduce the problem of the increasing radius of a circle?

    -The script introduces the problem by stating that the radius of a circle is increasing at a non-zero rate and the goal is to understand the implications of this expansion on the circle's area and circumference.

  • What is the formula used to express the area of a circle in the script?

    -The formula used to express the area of a circle in the script is \(A = \pi r^2\), where \(A\) is the area and \(r\) is the radius of the circle.

  • What is the differential equation derived from the area formula to find the rate of increase of the area?

    -The differential equation derived from the area formula is \(dA/dt = 2\pi r \cdot dr/dt\), which represents the rate of increase of the area with respect to time.

  • How is the rate of increase of the area related to the rate of increase of the circumference in the script?

    -In the script, it is stated that the rate of increase of the area is numerically equal to the rate of increase of the circumference, which means \(dA/dt = dC/dt\).

  • What is the formula for the circumference of a circle mentioned in the script?

    -The formula for the circumference of a circle mentioned in the script is \(C = 2\pi r\), where \(C\) is the circumference and \(r\) is the radius.

  • What is the process used in the script to find the rate of increase of the area in terms of the rate of increase of the radius?

    -The process used in the script involves setting up the differential equations for the area and circumference, and then equating the derivatives to find the relationship between the rates of change.

  • What is the final conclusion reached in the script regarding the value of the radius?

    -The final conclusion reached in the script is that the radius \(r\) must equal 1, after simplifying the equation derived from the relationship between the rates of increase of the area and circumference.

  • How does the script emphasize the importance of using correct mathematical notation?

    -The script emphasizes the importance of using correct mathematical notation by pointing out the need to distinguish between the derivative (denoted by a prime) and the rate of change with respect to time (denoted by \(d/dt\)).

  • What is the significance of the rate of increase of the area being numerically equal to the rate of increase of the circumference?

    -The significance is that it establishes a direct relationship between the rate at which the size of the circle changes (through its radius) and the corresponding change in its perimeter and area, which can be useful in various mathematical and real-world applications.

  • How can the information from the script be applied to solve related problems?

    -The information from the script can be applied to solve problems that involve understanding or calculating the dynamics of a circle's size changes, such as predicting the growth of a circular object over time or determining the expansion rate of a circular shape in various scientific and engineering contexts.

Outlines
00:00
πŸ“ Understanding the Expanding Circle Problem

The speaker introduces a mathematical problem involving a circle whose radius is increasing over time. They begin by visually representing the concept with a drawn circle and a radius. The main focus is on the rate of change of the circle's area, which is stated to be equal to the numerical value of the rate of change of the circle's circumference. The speaker uses the formula for the area of a circle (A = Ο€r^2) and the circumference (C = 2Ο€r) to set up an equation involving the derivatives with respect to time (dr/dt and dC/dt). The goal is to solve for the radius r at a given instant, and the speaker concludes that r equals one after simplifying the equation by dividing both sides by the rate of change of the radius (dr/dt) and other constants like Ο€ and 2.

Mindmap
Keywords
πŸ’‘radius
The radius of a circle is the distance from the center of the circle to any point on its circumference. In the context of the video, the radius is increasing at a non-zero rate, which is the foundation for the mathematical problem being discussed. The radius plays a crucial role in determining the size of the circle and is used in formulas such as the area and circumference calculations.
πŸ’‘circle
A circle is a shape with all points equidistant from a central point known as the center. It is a fundamental geometric figure that serves as the basis for the problem in the video. The properties of a circle, such as its radius and circumference, are central to the discussion and calculations performed in the script.
πŸ’‘rate of increase
The rate of increase refers to how quickly a quantity changes over time. In the video, it is used to describe the change in the radius of the circle and later the rate of change in the area and circumference of the circle. Understanding the rate of increase is essential for solving the problem as it involves taking derivatives and setting up equations based on these rates.
πŸ’‘area
The area of a shape is the amount of space enclosed within its boundaries. In the context of the video, the area of the circle is calculated using the formula A = Ο€r^2, where 'A' represents the area and 'r' is the radius of the circle. The rate of change of the area is a key part of the mathematical problem being solved, as it is set to be equal to the rate of change of the circumference.
πŸ’‘circumference
The circumference of a circle is the distance around the circle's edge. It is calculated using the formula C = 2Ο€r, where 'C' stands for the circumference and 'r' is the radius. In the video, the circumference is used to establish a relationship with the rate of increase of the circle's area, and its formula is essential for deriving the mathematical equation to solve for the radius.
πŸ’‘derivative
A derivative is a concept in calculus that represents the rate of change of a function with respect to a variable. In the video, derivatives are used to find the rate of change (or the derivative) of the area and circumference with respect to time, denoted as dA/dt and dC/dt. These derivatives are crucial for solving the problem and finding the relationship between the changing radius and the circle's properties.
πŸ’‘dimension
In mathematics, dimensions refer to the measurable extent of a particular space or shape, such as length, area, or volume. The video script briefly mentions dimensions while discussing the rate of increase in the area of the circle, implying the need to consider the units or dimensions when performing calculations and comparisons.
πŸ’‘pi (Ο€)
Pi, often denoted by the symbol 'Ο€', is a mathematical constant approximately equal to 3.14159. It is the ratio of a circle's circumference to its diameter. In the video, pi is used in the formulas for calculating the area (Ο€r^2) and circumference (2Ο€r) of the circle, which are central to the mathematical problem being discussed.
πŸ’‘mathematical problem
A mathematical problem is a question or task that requires the use of mathematical concepts and operations to find a solution. In the video, the mathematical problem involves a circle whose radius is increasing and finding the relationship between the rate of change of its area and circumference. The problem-solving process involves setting up and solving equations based on the given conditions.
πŸ’‘equation
An equation is a statement that asserts the equality of two expressions. In mathematics, it is often used to represent a relationship between different quantities. In the video, equations are set up to equate the rate of change of the circle's area with the rate of change of its circumference, leading to the solution for the radius of the circle.
πŸ’‘solve
To solve a mathematical problem means to find the answer or solution that satisfies the given conditions or equations. In the video, the process of solving involves identifying the correct relationships, setting up the appropriate equations, and performing the necessary calculations to arrive at the solution for the radius of the expanding circle.
Highlights

The problem involves a circle with a radius that is increasing at a non-zero rate.

The initial step is to represent the radius and acknowledge the expansion of the circle.

The derivative dr/dt is introduced to represent the rate of change of the radius.

The area of the circle is expressed as pi * r^2.

The circumference of the circle is given as 2 * pi * r.

The rate of increase in the area of the circle is numerically equal to the rate of increase in the circumference.

The derivative of the area (dA/dt) is expressed as 2 * pi * r * dr/dt.

The derivative of the circumference (dC/dt) is expressed as 2 * pi * dr/dt.

The equality of the rate of change of the area and circumference is emphasized.

The goal is to find the value of r at a given instant.

The equation dA/dt = dC/dt is used to solve for r.

By dividing both sides of the equation by dr/dt, pi, and 2, r is found to be equal to 1.

The solution process is explained in a step-by-step manner.

The mathematical approach to the problem is clear and logical.

The problem-solving method can be applied to similar geometrical and mathematical scenarios.

The transcript demonstrates a practical application of calculus in understanding geometrical changes.

The solution to the problem is obtained through the application of fundamental calculus concepts.

The transcript serves as an example of how to approach and solve a rate-related geometry problem.

Transcripts

Browse More Related Video

AP CALCULUS AB 2022 Exam Full Solution FRQ#4d

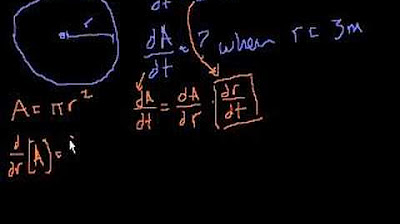
Rates-of-change (part 2)

Related Rate Problems - The Cube - Volume, Surface Area & Diagonal Length

AP CALCULUS AB 2022 Exam Full Solution FRQ#2d

How to solve a changing area of circle with related rates

Related Rates - Inflated Balloon & Melting Snowball Problem - Surface Area & Volume

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GeometryCalculusCircle PropertiesRate of ChangeRadius DynamicsArea CalculationCircumference FormulaMath ProblemEducational ContentAnalytical Approach