AP CALCULUS AB 2022 Exam Full Solution FRQ#2d
TLDRThe video script explains a related rates problem involving a vertical line moving at a constant rate along the base of a solid, changing the area of a cross-sectional square. The goal is to find the rate of change of the area when the line is at x = -0.5. The presenter establishes an expression for the area of the cross section (A(x) = (f(x) - g(x))^2), then differentiates this to find dA/dx. However, since the rate of change is needed with respect to time, the problem is approached as a related rates problem. The derivative at x = 0.5 is found using a graphing calculator, and the known dx/dt (7 units per second) is used to calculate dA/dt. The final answer is a negative value, indicating the area is decreasing at that rate.
Takeaways
- 📐 The problem involves a vertical line in the XY plane that moves horizontally to change the position of a square cross-section, which in turn changes its area.
- 🔵 The vertical line (purple) moves at a constant rate of 7 units per second, which is given as dx/dt.
- 🟢 The cross-section is a square, and its area (A) is represented by the square of the difference between two functions, f(x) - g(x), squared.
- 🧮 To find the rate of change of the area (da/dt), we first find da/dx by differentiating the expression for A with respect to x.
- 📈 The differentiation of the area function is done using a graphing calculator to find the derivative at a specific point, x = -0.5.
- 📊 The derivative at x = -0.5 (a') is found to be -1.32455 using the graphing calculator's dy/dx function.
- 🔴 The rate of change of the area with respect to time (da/dt) is then calculated by multiplying the derivative (da/dx) by the given rate of horizontal movement (dx/dt).
- ⏱️ The final calculation for da/dt at x = -0.5, using the values found, results in a value of -9.27 square units per second.
- 📌 The process is framed as a related rates problem, where the rate of change with respect to time is found by relating it to the known rate of change with respect to x.
- 📘 The expression for the area of the cross-section is A(x) = [f(x) - g(x)]^2, which is derived from the side length of the square cross-section.
- 🔬 The script demonstrates a step-by-step approach to solving calculus problems involving rates of change and related rates in a geometric context.
Q & A
What is the shape of the cross-sectional area described in the script?
-The cross-sectional area described in the script is a square.
How is the vertical line in the X Y plane moving?
-The vertical line is moving from left to right at a constant rate of 7 units per second.
What is the purpose of the vertical line's movement?
-The movement of the vertical line changes the position of the square, which in turn changes the area of the cross-section.
What is the expression for the area of the cross-section (A) in terms of x?
-The area of the cross-section A is given by the square of the difference between two functions, f(x) and g(x), so A = [f(x) - g(x)]^2.
What is the rate of change of the area with respect to time (dA/dt) that we are trying to find?
-We are trying to find the rate of change of the area when x is at -0.5 seconds.
How is the rate of change of the area with respect to x (dA/dx) related to the rate of change with respect to time (dA/dt)?
-The rate of change of the area with respect to time (dA/dt) is found by multiplying the rate of change with respect to x (dA/dx) by the rate at which x is changing with respect to time (dx/dt).
What is the given rate at which x is changing with respect to time (dx/dt)?
-The given rate at which x is changing with respect to time (dx/dt) is 7 units per second.
How does one find the derivative of the area function at a specific point (dA/dx)?
-The derivative of the area function at a specific point can be found by differentiating the expression for the area and then evaluating it at the given point, or by using a graphing calculator's derivative function.
What is the value of the derivative of the area function at x = -0.5?
-The value of the derivative of the area function at x = -0.5 is -1.324551.
How is the final rate of change of the area with respect to time (dA/dt) calculated?
-The final rate of change of the area with respect to time (dA/dt) is calculated by multiplying the derivative value at x = -0.5 by the rate of change of x with respect to time (dx/dt), which is -1.324551 * 7 units per second.
What is the final calculated rate of change of the area with respect to time (dA/dt) in square units per second?
-The final calculated rate of change of the area with respect to time (dA/dt) is -9.27 square units per second.
What does the negative sign in the rate of change of the area indicate?
-The negative sign in the rate of change of the area indicates that the area is decreasing over time at the point where x is -0.5.
Outlines
📐 Calculating the Rate of Change of a Cross-Sectional Area
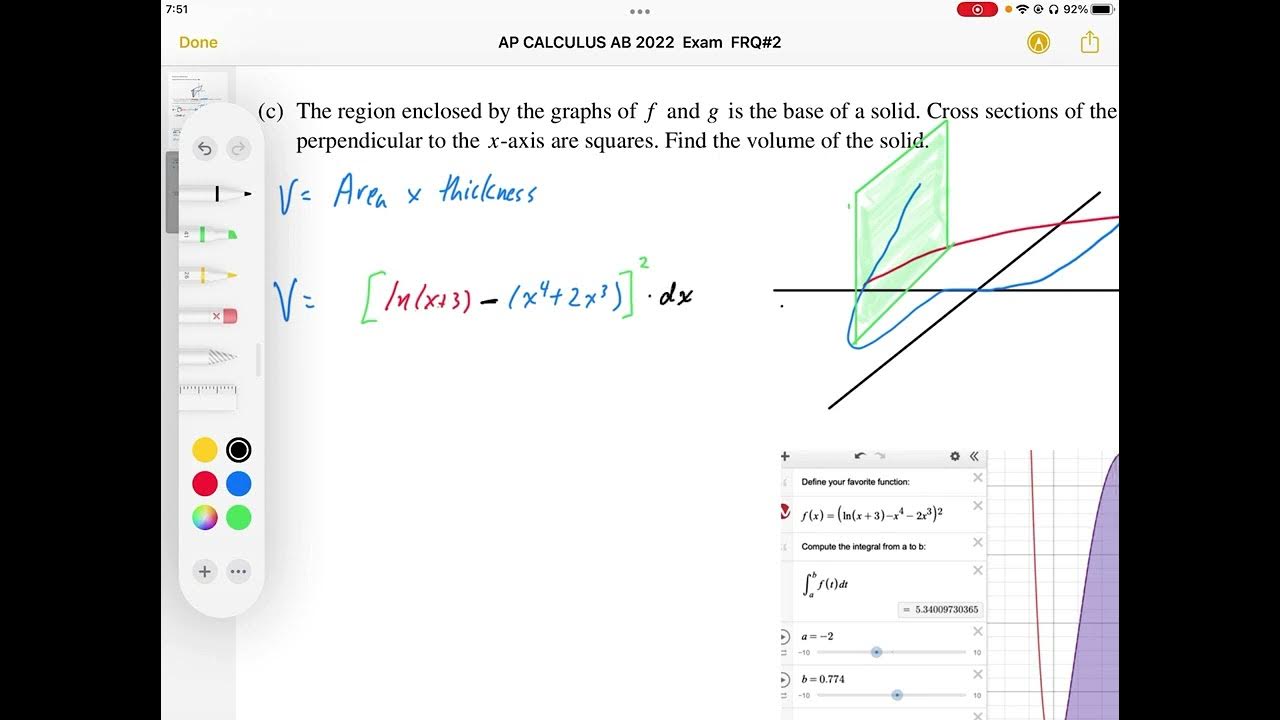
This paragraph introduces a geometry problem involving a vertical line moving along the base of a solid in the XY plane, which changes the position of a square cross-section, thereby altering its area. The vertical line moves at a constant rate of 7 units per second. The goal is to find the rate of change of the area of the cross-section when the line is at x = -0.5. To solve this, an expression for the area (A) is established as the square of the side length (s), which is the difference between an upper function (f(x)) and a lower function (g(x)). The task is to find dA/dt, which requires differentiating A with respect to x (dA/dx) and then multiplying by the known dx/dt. The differentiation is done at x = 0.5, and the derivative at this point is found using a graphing calculator, resulting in a slope value that is then multiplied by the rate of movement (dx/dt) to find dA/dt.
📉 Deriving the Final Rate of Change for the Cross-Sectional Area
The second paragraph continues the problem-solving process by finding the derivative (a') at x = -0.5 using the previously established expression from the graphing calculator. With the given dx/dt of seven units per second, the rate of change of the area (dA/dt) is calculated by multiplying the derivative value (a') by dx/dt. The result is a negative value, indicating a decrease in the area over time. The final calculated dA/dt is -9.27 square units per second, which represents the rate at which the area of the cross-section is changing when the vertical line is at x = -0.5.
Mindmap
Keywords
💡Vertical Line
💡Cross-Sectional Square
💡Rate of Change
💡Differentiation
💡Related Rate Problem
💡Graphing Calculator
💡Derivative
💡Constant Rate
💡Area Function
💡Expression
💡Calculus
Highlights
The vertical line in the XY plane travels from left to right along the base of a solid, changing the position of a cross-sectional square and thus its area
The rate of change of the area of the cross-section above the vertical line is to be found when x is at -0.5
An expression for the area of the cross-section (s^2) is established as the difference between the upper and lower functions squared
Differentiating the area expression with respect to x (da/dx) is required to find the rate of change of the area
The perspective is changed to a related rate problem to find da/dt by first finding da/dx and then using the known dx/dt
The rate of the vertical line moving to the right (dx/dt) is given as 7 units per second
Differentiating the area function at x = 0.5 using a graphing calculator yields a value of -1.32455
The derivative at x = 0.5 (a') represents the slope of the area function at that point
The change in area over time (da/dt) is found by multiplying the a' value at x = -0.5 by the dx/dt rate
The calculated da/dt value is -9.27151 square units per second
The vertical line's movement at a constant rate impacts the area of the cross-section
Finding the rate of change of the area requires differentiating the area expression with respect to x
The area function is graphed and its derivative at a specific point is calculated using a graphing calculator
The known dx/dt rate is used in conjunction with the area function's derivative to find the rate of change of the area
The final calculated da/dt value indicates the rate at which the area of the cross-section changes per second
The problem involves a solid with a cross-sectional square that changes position and area as a vertical line moves along its base
The area of the cross-section is expressed as the square of the difference between the upper and lower functions
Differentiating the area expression with respect to x and using the known dx/dt rate allows finding the rate of change of the area
A graphing calculator is used to graph the area function and calculate its derivative at a specific point
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: